LinearOptimization
LinearOptimization[f,cons,vars]
線形制約 cons に従って線形目的関数 f を最小化する変数 vars の値を求める.
LinearOptimization[c,{a,b}]
線形不等式制約 ![]() に従って線形目的関数
に従って線形目的関数 ![]() を最小化する実数ベクトル x を求める.
を最小化する実数ベクトル x を求める.
LinearOptimization[c,{a,b},{aeq,beq}]
線形等式制約 ![]() を含める.
を含める.
LinearOptimization[c,…,{dom1,dom2,…}]
LinearOptimization[…,"prop"]
解のどの特性 "prop"を返すべきか指定する.
詳細とオプション




- 線形最適化は,線形計画法(LP)および混合整数線形計画法(MILP)としても知られている.
- 線形最適化は,実変数,整数変数,あるいは複素変数で大域的にまた効率的に解くことができる凸最適化問題である.
- 線形最適化は主問題を解く
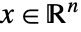 を求める. »
を求める. » -
最小化 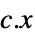
制約条件 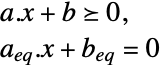
ただし 
- 混合整数線形最適化は,問題を解く
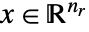 および
および 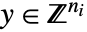 を求める.
を求める. -
最小化 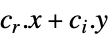
制約条件 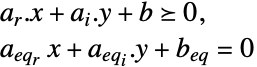
ただし 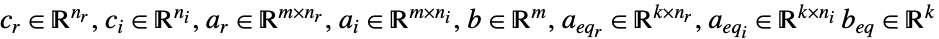
- LinearOptimizationは,目的関数が実数値のときは,
![x in TemplateBox[{}, Complexes]^n x in TemplateBox[{}, Complexes]^n](Files/LinearOptimization.ja/13.png) の問題を内部的に実変数
の問題を内部的に実変数 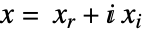 に変換して解く.ただし,
に変換して解く.ただし,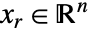 で
で 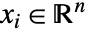 である.
である. - 変数指定 vars は,次のいずれかの形式で変数を与える要素のリストでなければならない.
-
v 名前が 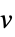 で次元が推測される変数
で次元が推測される変数v∈Reals 実スカラー変数 v∈Integers 整数スカラー変数 v∈Complexes 複素スカラー変数 v∈ℛ 幾何学領域  に制限されたベクトル変数
に制限されたベクトル変数v∈Vectors[n,dom]  または
または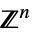 のベクトル変数
のベクトル変数v∈Matrices[{m,n},dom] 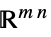 または
または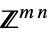 の行列変数
の行列変数 - 制約条件 cons は以下で指定できる.
-
LessEqual 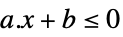
スカラー不等式 GreaterEqual 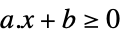
スカラー不等式 VectorLessEqual 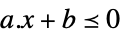
ベクトル不等式 VectorGreaterEqual 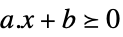
ベクトル不等式 Equal 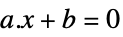
スカラー等式またはベクトル等式 Element 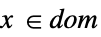
凸領域または領域要素 - LinearOptimization[f,cons,vars]では,f または cons で使用するパラメータを定義するために,parval の形式のパラメータ方程式を制約条件に入れることができる.ただし,par は vars には含まれず,val は数値または数値配列であるとする.
- 主最小化問題には関連する最大化問題(ラグランジュ双対問題)がある.双対最大値は常に主最小値以下なので,下界を与える.双対マキシマイザは,制約条件に対する最小値の感度変化を含む,主問題についての情報を与える.
- 線形最適化についてのラグランジュ双対問題は以下で与えられる. »
-
最大化 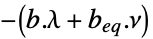
制約条件 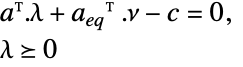
ただし 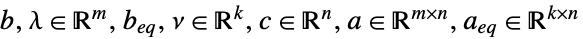
- 線形最適化については,強双対性が常に成り立つ.つまり,主最小化問題に解があれば双対最大化問題にも解があり,双対最大値は主最小値に等しい.
- 可能な解の特性"prop"には以下がある.
-
"PrimalMinimizer" 
目的関数を最小化する変数値のリスト "PrimalMinimizerRules" 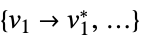
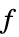 を最小化する変数の値 vars={v1,…}
を最小化する変数の値 vars={v1,…}"PrimalMinimizerVector" 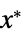
 を最小化するベクトル
を最小化するベクトル"PrimalMinimumValue" 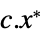
最小値 
"DualMaximizer" 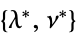
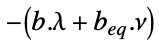
"DualMaximumValue" 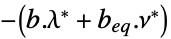
双対最大値 "DualityGap" 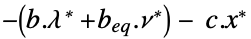
双対最適値と主最適値の差(強双対性により0) "Slack" 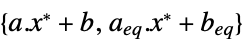
制約条件スラックベクトル "ConstraintSensitivity" 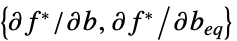
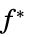 の制約条件の摂動に対する感度
の制約条件の摂動に対する感度"ObjectiveVector" 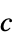
線形目的ベクトル "LinearInequalityConstraints" 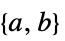
線形不等式制約の行列およびベクトル "LinearEqualityConstraints" 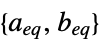
線形等式制約の行列およびベクトル {"prop1","prop2",…} いくつかの解の特性 - 次は,使用可能なオプションである.
-
MaxIterations Automatic 使用する最大反復回数 Method Automatic 使用するメソッド PerformanceGoal $PerformanceGoal パフォーマンスのどの局面について最適化するか Tolerance Automatic 内部計算の許容度 WorkingPrecision Automatic 内部計算の精度 - オプションMethod->method を使って使用するメソッドを指定することができる.次は使用可能なメソッドである.
-
Automatic メソッドを自動的に選択する "Simplex" シンプレックス法 "RevisedSimplex" 改訂シンプレックス法 "InteriorPoint" 内点法(機械精度のみ) "CLP" COINライブラリ線形計画法(機械精度のみ) "MOSEK" 商用MOSEK線形最適化ソルバ "Gurobi" 商用Gurobi線形最適化ソルバ "Xpress" 商用Xpress形最適化ソルバ - WorkingPrecision->Automaticのときは,機械精度でしか使えないメソッドが指定されていない限り,入力引数の精度から自動的に精度が取られる.機械精度でしか使えないメソッドには機械精度が使用される.

例題
すべて開くすべて閉じる例 (3)
スコープ (32)
基本的な用法 (16)
VectorLessEqualを使っていくつかのLessEqual不等式制約を一度に表す:
![]() v<=
v<=![]() を使ってコンパクトな形式でベクトル不等式を入力する:
を使ってコンパクトな形式でベクトル不等式を入力する:
VectorGreaterEqualを使っていくつかのGreaterEqual不等式制約を一度に表す:
![]() v>=
v>=![]() を使ってコンパクトな形式でベクトル不等式を入力する:
を使ってコンパクトな形式でベクトル不等式を入力する:
Equalを使っていくつかの不等式制約を一度に表す:
スカラー不等式とベクトル不等式を組み合せて制約条件を指定する:
Indexedを使ってベクトル変数,例えば ![]() の成分にアクセスする:
の成分にアクセスする:
定数パラメータ方程式を使って目的関数と制約条件の係数を指定する:
定数パラメータ方程式を使っていくつかの制約条件の係数を指定する:
必要な場合は,Vectors[n]を使ってベクトル変数の次元を指定する:
NonNegativeReals (![]() )を使って非負の制約条件を指定する:
)を使って非負の制約条件を指定する:
NonPositiveReals (![]() )を使って非正の制約条件を指定する:
)を使って非正の制約条件を指定する:
整数変数 (4)
Integersを使って整数領域の制約を指定する:
Vectors[n,Integers]を使って,ベクトル変数に整数領域の制約を指定する:
NonNegativeIntegers (![]() )を使って非負の整数制約を指定する:
)を使って非負の整数制約を指定する:
NonPositiveIntegers (![]() )を使って非正の整数制約を指定する:
)を使って非正の整数制約を指定する:
複素変数 (2)
Complexesを使って複素変数を指定する:
主モデル特性 (3)
双対モデル特性 (3)
オプション (9)
Method (5)
MachinePrecision入力のデフォルトメソッドは"CLP"である:
任意または無限のWorkingPrecisionのデフォルトメソッドは"Simplex"である:
MachinePrecision入力にはすべてのメソッドを使うことができる:
任意精度および無限精度の入力に"Simplex"および"RevisedSimplex"を使うことができる:
メソッドによって強みが異なるが,これは問題および実装に依存する:
"Simplex"および "RevisedSimplex"は小さい密な問題に向いている:
"InteriorPoint"および"CLP"は大きい疎な問題に向いている:
"InteriorPoint"法または"CLP"法は,問題が実行不可能あるいは非有界かどうかを明らかにできないかもしれない:
"Simplex"および"RevisedSimplex"は非有界問題あるいは実行不可能な問題が検知できる:
複数の最適解がある問題については,メソッドによって結果が異なることがある:
Tolerance (2)
WorkingPrecision (2)
LinearOptimizationは入力からWorkingPrecisionを推測する:
MachinePrecisionの入力はMachinePrecisionの出力を与える:
LinearOptimizationはよ高い作業精度で結果を計算することができる:
指定された精度が入力引数の精度よりも低い場合は,メッセージが出される:
アプリケーション (34)
基本的なモデリング変換 (8)
データフィッティング問題 (4)
![]() を最小化することで,離散データに対する強力な線形フィットを求める.補助変数
を最小化することで,離散データに対する強力な線形フィットを求める.補助変数 ![]() を使うと,この問題は制約条件
を使うと,この問題は制約条件![]() に従って
に従って![]() を最小化するものに変換されるが,これは線形最適化問題である:
を最小化するものに変換されるが,これは線形最適化問題である:
線のプロットは,これが外れ値に対して強力であることを示している:
LeastSquaresを使って得られたフィットと比較する:
線が最初のデータ点を通るように![]() を最小化することで線形フィットを求める:
を最小化することで線形フィットを求める:
制約条件a〚1〛.xb〚1〛を加えると,強制的にこの線が最初の点を通るようにできる:
プロットは,線が強力なフィットを保持しながら最初のデータ点を通過することを示している:
![]() を最小化することで非線形離散データに対する強力なフィットを求める.ノイズのあるデータを生成する:
を最小化することで非線形離散データに対する強力なフィットを求める.ノイズのあるデータを生成する:
![]() を最小化することで離散データに対する線形フィットを求める.
を最小化することで離散データに対する線形フィットを求める.![]() なので,スカラー補助変数
なので,スカラー補助変数 ![]() を導入することで問題を制約条件
を導入することで問題を制約条件![]() に従って
に従って ![]() を最小化するものに変換できる:
を最小化するものに変換できる:
関数Fitを直接使って係数を計算することができる:
分類問題 (3)
製造問題 (3)
企業の収益を最大にする製造製品の組合せを求める.この企業は3つの製品を製造している.製品1つあたりの収益,製品1つあたりの費用,最大生産量は以下の通りである:
各製品は4つの機械を組み合せて作られている.各製品についての機械の使用時間は以下の通りである:
製品 ![]() についての収益は,単価から費用を引いて単位数
についての収益は,単価から費用を引いて単位数 ![]() を掛けたものである:
を掛けたものである:
同じ企業が収益に最も大きい影響を与える製造能力の変更を知りたがっている.最適な製品の組合せと収益は,前の例で以下で与えられる:
収益に対する製造能力の変化の分析に必要なすべてのデータを抽出する:
感度は各制約条件に対する収益の導関数を与える.何らかの感度がある制約条件を抽出する:
製品1,製品2,あるいは両方の製造能力が変化しても収益は増加しない:
会社の利益を最大にするために,製造する製品の組合せを求める.この会社は ![]() の3つの製品を製造している.単位あたりの収益は以下の通りである:
の3つの製品を製造している.単位あたりの収益は以下の通りである:
工場のは100日しか稼働しない.各単位の製造にはそれぞれ![]() 日かかる:
日かかる:
各製品には金と錫が使われている.入手可能な金と錫の合計はそれぞれ30単位と200単位である:
各製品を製造するとすると,会社にはセットアップ費用がかかる:
セットアップ費用が比較的高額なため,全く製造しない方がよい製品があるかもしれない.製品 ![]() が製造された場合には
が製造された場合には ![]() ,それ以外の場合は
,それ以外の場合は ![]() となるような決定変数
となるような決定変数 ![]() を設定する.
を設定する.![]() という制限で,
という制限で,![]() に他の制約を加えずに
に他の制約を加えずに ![]() が0の場合は
が0の場合は ![]() となるようにする:
となるようにする:
輸送問題 (1)
最適割当て問題 (2)
ジェダイ騎士団はドゥークー率いる分離派と戦っている.ドゥークーと2人の将軍のアサージ・ヴェントレスとグリーヴァス将軍は3つのアウターコロニーを攻撃した.ジェダイ騎士団はアウターコロニーを助けるために3人のジェダイを派遣した.ジェダイ ![]() がシス
がシス ![]() に勝つ勝率を
に勝つ勝率を ![]() とする:
とする:
![]() を行列変数とする.ジェダイ
を行列変数とする.ジェダイ ![]() がシス
がシス ![]() と戦う場合の
と戦う場合の ![]() は1でその他は0である.費用関数は
は1でその他は0である.費用関数は ![]() で与えられる負けの期待数で,Inactive[Times]を使って構築される:
で与えられる負けの期待数で,Inactive[Times]を使って構築される:
アウターコロニーははるか遠くにあるので,各ジェダイに1人のシスが割り当てられるだけかもしれない.また,![]() は0か1なので
は0か1なので ![]() である:
である:
負けを最小にするための,シスに対する適切なジェダイを求める:
これは,オビ=ワン・ケノービがグリーヴァス将軍のもとに,メイス・ウィンドゥがアサージ・ヴェントレスのもとに,キ=アディ=ムンディがドゥークーのもとに送られることを意味する.期待される負けの数は以下である:
総重量を最小化する,2つの集合 ![]() と
と ![]() の間の二部グラフマッチング問題を解く:
の間の二部グラフマッチング問題を解く:
![]() を行列変数とする,ただし,
を行列変数とする,ただし,![]() は
は ![]() が
が ![]() とマッチするとき1で,それ以外の場合は0である.マッチングの総重量は
とマッチするとき1で,それ以外の場合は0である.マッチングの総重量は![]() で与えられ,Inactive[Times]を使って構築される:
で与えられ,Inactive[Times]を使って構築される:
LinearOptimizationを使ってこの問題を解く:
マッチング置換は行列 ![]() をグラフに変換することで抽出することができる.Roundを使ってメソッドによる数値誤差のために起こるかもしれない小さい値を切り捨てる:
をグラフに変換することで抽出することができる.Roundを使ってメソッドによる数値誤差のために起こるかもしれない小さい値を切り捨てる:
在庫管理問題 (2)
費用を最小にするために小売店が1週間に発注しなければならない製品 ![]() についての在庫を求める.
についての在庫を求める.![]() を週
を週 ![]() の初めに利用可能な在庫とする.
の初めに利用可能な在庫とする.![]() は週
は週 ![]() の初めに問屋から受け取る仕入れ注文とする.問屋からの1単位の購入費用は$3である:
の初めに問屋から受け取る仕入れ注文とする.問屋からの1単位の購入費用は$3である:
過剰または負の在庫の保存費用は単位あたり$1である.在庫費用は![]() で,これは線形ではなく
で,これは線形ではなく ![]() として表すことができる:
として表すことができる:
![]() を週
を週 ![]() の初めの需要とする.52週間の需要は,
の初めの需要とする.52週間の需要は,![]() について
について![]() で与えられる.店の在庫は
で与えられる.店の在庫は ![]() となる:
となる:
週0に存在する在庫は ![]() 単位で仕入れ注文は
単位で仕入れ注文は ![]() 単位である.店は1週間に10単位を超えて問屋から購入することはできない:
単位である.店は1週間に10単位を超えて問屋から購入することはできない:
費用を最小にするための,店に保存する最適な在庫と問屋からの注文を求める:
次は,在庫,仕入れ注文,需要のプロットである.これを見ると26週以降には在庫を抱える必要がなく,したがって在庫費用が最小化されることが分かる:
小売店が取り寄せ注文なしで費用を最小にするために注文すべき,1週間あたりの製品 ![]() の在庫を求める.
の在庫を求める.![]() を週
を週 ![]() の初めに問屋から受け取る仕入れ注文とする.問屋からの1単位の仕入れ費用は$3である:
の初めに問屋から受け取る仕入れ注文とする.問屋からの1単位の仕入れ費用は$3である:
![]() を週
を週 ![]() の初めの需要とする.52週間の需要は
の初めの需要とする.52週間の需要は![]() について
について![]() で与えられる.店の在庫は
で与えられる.店の在庫は ![]() である:
である:
初期在庫はs ![]() 単位と
単位と ![]() 単位で,問屋からの最大購入量は10単位である:
単位で,問屋からの最大購入量は10単位である:
この会社は,取り寄せ注文を確実になくしたい,つまり ![]() にしたい:
にしたい:
費用を最小にする店に保存する最適在庫と問屋への注文を求める:
次のプロットは,取り寄せ注文を回避するためには,需要に見合うように最初の数週に過剰在庫を購入すべきであることを示している.20週から21週には在庫費用がなくなる:
構造最適化問題 (2)
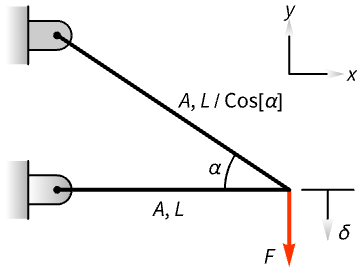
応力と変位の制約条件に従って,2ビームトラスの重量を最小にする:
重量は ![]() である.ただし,
である.ただし,![]() は密度,
は密度,![]() および
および ![]() は棒1と棒2の断面積である.この問題のために
は棒1と棒2の断面積である.この問題のために ![]() を仮定する:
を仮定する:
応力 ![]() ,ただし
,ただし ![]() は棒に沿って働く力で,指定された応力
は棒に沿って働く力で,指定された応力 ![]() より小さくなければならない:
より小さくなければならない:
自由ノードにおけるずれは![]() .である.棒の軸に沿ったこのずれの成分はずれ
.である.棒の軸に沿ったこのずれの成分はずれ ![]() と等しくなければならない.ただし,
と等しくなければならない.ただし,![]() はヤング率である:
はヤング率である:
自由ノードの縦のずれは与えられた ![]() より小さくなければならない:
より小さくなければならない:
使用されている材料はアルミニウムである.設計パラメータは以下である:
トラスの重量が180kgを超えない角度と長さの範囲を求める:
2ビームトラスの重量を応力とずれの制約条件に従って最小にし,トラスの設計に大きく影響する制約条件を求める:
重量は ![]() である.ただし,
である.ただし,![]() は密度,
は密度,![]() および
および ![]() は棒1と棒2の断面積である.この問題のために
は棒1と棒2の断面積である.この問題のために![]() を仮定する:
を仮定する:
使用されている素材はアルミニウムである.設計パラメータは以下である:
順次線形最適化 (1)
数独ゲーム (3)
![]() を部分正方形
を部分正方形![]() の変数とし,
の変数とし,![]() をベクトル
をベクトル ![]() の要素
の要素 ![]() とする.
とする.![]() のとき,
のとき,![]() には数
には数 ![]() が入る.各
が入る.各 ![]() には1つの数字しか入らないので,
には1つの数字しか入らないので,![]() には1つの非零の要素しか入らない.つまり,
には1つの非零の要素しか入らない.つまり,![]() である:
である:
各行にはすべての数がなければならない.つまり,![]() である.ここで,
である.ここで,![]() は1の9次元のベクトルである:
は1の9次元のベクトルである:
それぞれの3×3ブロックにはすべての数が入らなければならない.つまり,![]() である:
である:
既知の値を制約条件に変換する.もし部分正方形 ![]() に
に ![]() が入るのなら,
が入るのなら,![]() である:
である:
最初の行をランダムに指定することで,ランダムな数独ボードを生成する.上で説明した手続きに従ってソルバ関数を定義する:
ボードをランダムに生成し,一度に1つの要素を削除して数独パズルを生成する.数独パズルを解く関数を定義する.数独ボード上に負の数が指定されると,この関数はその数がその場所には入れられないと仮定する:
ボードの最初の行をランダムに指定することでランダムな参照数独ボードを生成する:
解の一意性を損なうことなしに削除できる要素がなくなるまで,ランダムに選択した要素を一度に1つずつボードから削除していく.この削除は,削除された要素が削除された数を持つことはできないという条件を加えて数独パズルを解くことで検証することができる.実行可能な解が求まったならば,その場所にあった数は一意的ではなく,その要素は残しておくことができる.それ以外の場合は,その要素がボードから削除される:
グラフ彩色問題 (1)
集合被覆問題 (3)
病院の救急救命室(ER)でリストにある処置を行うためにERに待機させなければならない医師の組合せを求める.各医師は特定数の処置しか行えないものとする:
![]() を医師
を医師 ![]() が待機している場合に
が待機している場合に ![]() となるような決定ベクトルとする.目的は費用を最小にすることである:
となるような決定ベクトルとする.目的は費用を最小にすることである:
6つの地区からなる都市に,各地区から15分以内の場所に消防署があるようにするために建設しなければならない消防署の最低数を求める.ある地区から隣の地区までの運転時間は以下の通りである:
![]() を,地区
を,地区 ![]() に消防署が建設された場合に
に消防署が建設された場合に ![]() となるような決定ベクトルとする.目的は消防署の数を最低にすることである:
となるような決定ベクトルとする.目的は消防署の数を最低にすることである:
各地区から15分以内の場所に少なくとも1つの消防署がなければならない:
ある会社がその6つの小売店に商品を供給するために建設しなければならない倉庫の最小数を求める.この会社は倉庫の候補地を5つ選んだ.各小売店に各倉庫から商品を供給するための費用は以下の通りである:
![]() を,倉庫
を,倉庫 ![]() が建設されたなら
が建設されたなら ![]() となる決定変数とする.
となる決定変数とする.![]() は倉庫
は倉庫 ![]() が小売店
が小売店 ![]() に供給する商品の割合を表す.目的は費用を最小にすることである:
に供給する商品の割合を表す.目的は費用を最小にすることである:
巡回セールスマン問題 (1)
セールスマンが ![]() 都市を1回だけ通る最短経路を求める.場所を生成する:
都市を1回だけ通る最短経路を求める.場所を生成する:
都市 ![]() から都市
から都市 ![]() までの距離を
までの距離を ![]() とする.
とする.![]() は,
は,![]() なら経路が都市
なら経路が都市 ![]() から都市
から都市 ![]() へ向かう決定変数である.目的は距離を最短にすることである:
へ向かう決定変数である.目的は距離を最短にすることである:
セールスマンは厳密に1つの都市から来て厳密に1つの都市へ行くことができる:
セールスマンは1回のツアーですべての場所を回らなければならない:
FindShortestTourを使ってより効率的に巡回セールスマン問題を解く:
特性と関係 (9)
LinearOptimizationは目的関数の大域的最小値を与える:
Minimizeは,線形最適化問題の大域的厳密結果も与える:
NMinimizeを使い,大域メソッドを使って近似結果を得ることができる:
FindMinimumを使い,局所的メソッドを使って近似結果を得ることができる:
LinearFractionalOptimizationは問題を解くためにLinearOptimizationを使う:
QuadraticOptimizationはLinearOptimizationの一般化である:
SecondOrderConeOptimizationはLinearOptimizationの一般化である:
SemidefiniteOptimizationはLinearOptimizationの一般化である:
ConicOptimizationはLinearOptimizationの一般化である:
考えられる問題 (6)
狭義の不等式を使って指定された制約条件は満足されないかもしれない:
理由は,LinearOptimizationが ![]() を解くからである:
を解くからである:
ミニマイザはIndeterminateである:
ミニマイザはIndeterminateである:
混合整数問題に関する双対関連の解の特性は得られないかもしれない:
複素数値を含む制約条件はベクトル不等式で指定する必要がある:
GreaterEqualだけを使ってもうまく行かない:
テキスト
Wolfram Research (2019), LinearOptimization, Wolfram言語関数, https://reference.wolfram.com/language/ref/LinearOptimization.html (2020年に更新).
CMS
Wolfram Language. 2019. "LinearOptimization." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2020. https://reference.wolfram.com/language/ref/LinearOptimization.html.
APA
Wolfram Language. (2019). LinearOptimization. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/LinearOptimization.html