MinLimit
MinLimit
詳細とオプション
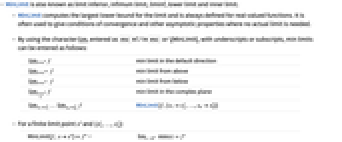
- MinLimitは，下極限としても知られている．
- MinLimitは，極限の最大の下界を計算し，常に実数値関数について定義される．収束条件や実際に極限が存在するかどうかに依存しないその他の漸近的特性を与えるためにしばしば使われる．
- 最小極値は，記号（
mlim
または\[MinLimit]で入力）を真下付き文字あるいは下付き文字と一緒に使って次のように入力する． -
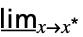fデフォルト方向への最小極限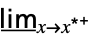 
f上からの最小極限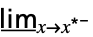 
f下からの最小極限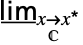 
f複素平面上の最小極限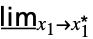 
…
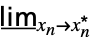fMinLimit[f,{x1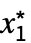 
,…,xn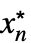
}] - 有限極限点 x*と{
,…,
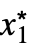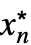}について -
MinLimit[f,xx*]f* ![TemplateBox[{{min, (, epsilon, )}, epsilon, 0, +, {Direction, ->, {-, 1}}}, LimitWithSuperscript, DisplayFunction -> ({Sequence[{Sequence["lim"], _, DocumentationBuild`Utils`Private`Parenth[{#2, ->, {#3, ^, DocumentationBuild`Utils`Private`Parenth[#4]}}, LimitsPositioning -> True]}], #1} & ), InterpretationFunction -> ({Limit, [, {#1, ,, {#2, ->, #3}, ,, #5}, ]} & )]=f^*](Files/MinLimit.ja/24.png "TemplateBox[{{min, (, epsilon, )}, epsilon, 0, +, {Direction, ->, {-, 1}}}, LimitWithSuperscript, DisplayFunction -> ({Sequence[{Sequence[\"lim\"], _, DocumentationBuild`Utils`Private`Parenth[{#2, ->, {#3, ^, DocumentationBuild`Utils`Private`Parenth[#4]}}, LimitsPositioning -> True]}], #1} & ), InterpretationFunction -> ({Limit, [, {#1, ,, {#2, ->, #3}, ,, #5}, ]} & )]=f^*")
MinLimit[f,{x1,…,xn}{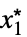 
,…,
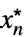}]f* ![TemplateBox[{{min, (, epsilon, )}, epsilon, 0, +, {Direction, ->, {-, 1}}}, LimitWithSuperscript, DisplayFunction -> ({Sequence[{Sequence["lim"], _, DocumentationBuild`Utils`Private`Parenth[{#2, ->, {#3, ^, DocumentationBuild`Utils`Private`Parenth[#4]}}, LimitsPositioning -> True]}], #1} & ), InterpretationFunction -> ({Limit, [, {#1, ,, {#2, ->, #3}, ,, #5}, ]} & )]=f^*](Files/MinLimit.ja/27.png "TemplateBox[{{min, (, epsilon, )}, epsilon, 0, +, {Direction, ->, {-, 1}}}, LimitWithSuperscript, DisplayFunction -> ({Sequence[{Sequence[\"lim\"], _, DocumentationBuild`Utils`Private`Parenth[{#2, ->, {#3, ^, DocumentationBuild`Utils`Private`Parenth[#4]}}, LimitsPositioning -> True]}], #1} & ), InterpretationFunction -> ({Limit, [, {#1, ,, {#2, ->, #3}, ,, #5}, ]} & )]=f^*")
- この定義は，1変量の f[x]についてはmin[ϵ]MinValue[{f[x],0<
![TemplateBox[{{x, -, {x, ^, *}}}, Abs]](Files/MinLimit.ja/28.png "TemplateBox[{{x, -, {x, ^, *}}}, Abs]")
<ϵ},x]，多変量の f[x1,…,xn]についてはmin[ϵ]MinValue[{f[x1,…,xn],0<![TemplateBox[{{{, {{{x, _, {(, 1, )}}, -, {x, _, {(, 1, )}, ^, *}}, ,, ..., ,, {{x, _, n}, -, {x, _, {(, n, )}, ^, *}}}, }}}, Norm]](Files/MinLimit.ja/29.png "TemplateBox[{{{, {{{x, _, {(, 1, )}}, -, {x, _, {(, 1, )}, ^, *}}, ,, ..., ,, {{x, _, n}, -, {x, _, {(, n, )}, ^, *}}}, }}}, Norm]")
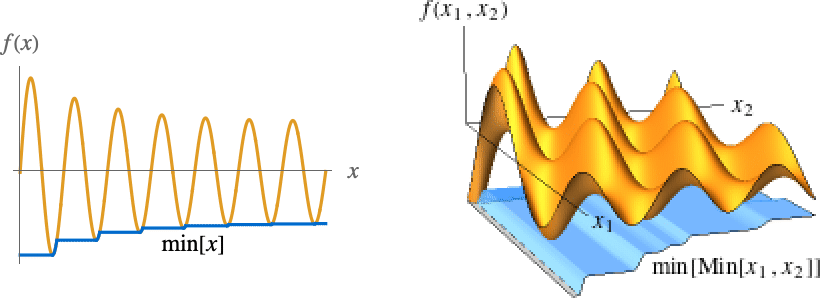
<ϵ},{x1,…,xn}]の最大包絡線が使われる．関数min[ϵ]は ϵ0のとき単調増加なので常に極限を持つ．この極限は±∞である場合もある． - 次の図ではmin[
![TemplateBox[{{x, -, {x, ^, *}}}, Abs]](Files/MinLimit.ja/30.png "TemplateBox[{{x, -, {x, ^, *}}}, Abs]")
]とmin[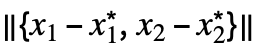
]が青くなっている． - 無限極限点 x*∞については，1変量の f についてはmin[ω]MinValue[{f[x],x>ω},x]，多変量の f についてはmin[ω]MinValue[{f[x1,…,xn],x1>ω∧⋯∧xn>ω},{x1,…,xn}]の最小包絡線が使われる．関数min[ω]は ω∞ のとき単調増加なので，常に極限を持つ．
- 次の図ではmin[x]とmin[Min[x1,x2]]が青くなっている．
- 最小極限が求まらなかったとき，MinLimitは未評価で返される．
- 次は使用可能なオプションである．
-
Assumptions $Assumptions パラメータについての仮定 Direction Reals 極限点に近付く方向 GenerateConditions Automatic パラメータについての条件を生成するかどうか Method Automatic 使用するメソッド PerformanceGoal "Quality" パフォーマンスのどの面について最適化するか - 次はDirectionの可能な設定である．
-
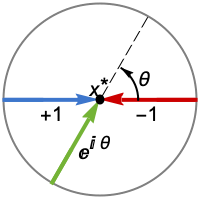
Reals または "TwoSided" 両実数方向から "FromAbove" または -1 上から，つまりより大きい値から "FromBelow" または +1 下から，つまりより小さい値から Complexes すべての複素方向から Exp[ θ]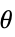 
の方向{dir1,…,dirn} 方向 diriを変数 xiに独立で使う - x*におけるDirectionExp[ θ]は曲線の接線が極限点 x*に近付く方向を示している．
- 次はGenerateConditionsの可能な設定値である．
-
Automatic 一般的ではない条件のみ True すべての条件 False 条件なし None 条件が必要な場合は未評価で返す - PerformanceGoalの可能な設定には，$PerformanceGoal，"Quality"，"Speed"がある．"Quality"設定のとき，MinLimitは，一般に，より多くの問題を解いたりより簡単な結果を生成したりするが，より多くの時間とメモリが必要になる可能性がある．
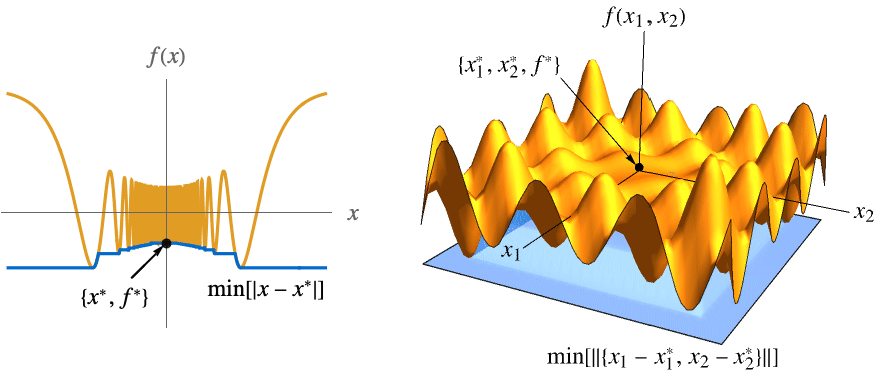
例題
すべて開く すべて閉じる例 (3)
MinLimit[Sin[x] + 1 / x, x -> ∞]Plot[{Sin[x] + 1 / x, -1}, {x, 0, 30}, PlotStyle -> {Automatic, Dashed}]MinLimit[(1/x), x -> 0]Plot[(1/x), {x, -1, 1}]MinLimit[RealAbs[x] / x, x -> 0, Direction -> "FromAbove"]MinLimit[RealAbs[x] / x, x -> 0, Direction -> "FromBelow"]MinLimit[RealAbs[x] / x, x -> 0]Plot[RealAbs[x] / x, {x, -1, 1}]スコープ (35)
基本的な用法 (5)
MinLimit[Sin[x], x -> π / 2]MinLimit[x / (x - 2a), x -> a]-Infinityにおける最小極限を求める：
MinLimit[3x ^ 2 / (x ^ 2 - 2), x -> -∞]
MinLimit[(y/x + y), {y -> 0, x -> 0}]
MinLimit[(y/x + y), {x -> 0, y -> 0}]
MinLimit[(y/x + y), {x, y} -> {0, 0}]極限のタイプセット (4)
mlim
を使って 記号を入力し，
を使って真下付き文字を作る：
Underscript[, x -> 0](x/x^3 + x^2)上付き文字の
または
を極限点に付けることで，上からまたは下からの極限を取る：
Underscript[, x -> 0^ + ](x/x^3 + x^2)
を使って真上付き文字を作る：Underscript[, x -> 0^ - ](x/x^3 + x^2)RealsあるいはComplexesの方向を指定するときは，記号の真下付き文字として定義域を入力する：
Underscript[, xUnderscript[ -> , ℂ]0]Abs[x]
->
で規則を入力し，
で真下付き文字を作り，
reals
とタイプして
を入力する：
Underscript[, xUnderscript[ -> , ℝ]0]Abs[x]TraditionalFormによる表示：
MinLimit[f[x], x -> a, Direction -> Reals]//TraditionalForm初等関数 (10)
MinLimit[a x^2 + b x + c, x -> 2]MinLimit[4 x ^ 3 - 100x, x -> ∞]MinLimit[4 x ^ 3 - 100x, x -> -∞]Plot[4 x ^ 3 - 100x + 1, {x, -10, 10}]MinLimit[(x^2 - 1/x - 1), x -> 1]Plot[{(x^2 - 1/x - 1), 2}, {x, 0, 2}, PlotTheme -> "DashedLines"]MinLimit[(x^2 + 1/x - 1), x -> 1]Plot[(x^2 + 1/x - 1), {x, 0, 2}, ExclusionsStyle -> Directive[StandardMagenta, Thick, Dashed]]±Infinityにおける有理関数：
MinLimit[1 / x, x -> ∞]Plot[{1 / x, 0}, {x, -10, 10}, PlotTheme -> "DashedLines", PlotRange -> 1]MinLimit[(x^2 + 1/2x + 2), x -> ∞]Plot[(x^2 + 1/2x + 2), {x, 0, 10}]MinLimit[(x^2 + 1/x^2 + 2), x -> -∞]Plot[{(x^2 + 1/x^2 + 2), 1}, {x, -5, 5}, PlotTheme -> "DashedLines"]MinLimit[CubeRoot[x], x -> -1]MinLimit[3(x ^ a - a x + a - 1) / (x - 1) ^ 2, x -> 1, Assumptions -> a∈ℝ]MinLimit[Sqrt[x ^ 2 + 3x] - Sqrt[x ^ 2 + 2x], x -> ∞]Plot[{Sqrt[x ^ 2 + 3x] - Sqrt[x ^ 2 + 2x], 1 / 2}, {x, 0, 20}, PlotRange -> All, PlotTheme -> "DashedLines"]MinLimit[Tan[x], x -> π / 2]MinLimit[Tan[x], x -> π / 2, Direction -> "FromBelow"]Plot[Tan[x], {x, 0, Pi}, ExclusionsStyle -> Directive[StandardMagenta, Thick, Dashed]]MinLimit[Sin[1 / x], x -> 0]Plot[Sin[1 / x], {x, -.1, .1}]±Infinityにおける三角関数：
MinLimit[Sin[x], x -> ∞]MinLimit[x Sin[x], x -> ∞]Plot[x Sin[x], {x, 0, 50}]Underscript[, x -> 0](ArcSin[x]/x)Plot[{ArcSin[x] / x, 1}, {x, -1, 1}, PlotTheme -> "DashedLines"]MinLimit[ArcTan[x ^ 3 - x], x -> -∞]Plot[{ArcTan[x ^ 3 - x], -Pi / 2, Pi / 2}, {x, -5, 5}, PlotTheme -> "DashedLines"]MinLimit[Exp[(1/x)], x -> 0]Plot[Exp[1 / x], {x, -5, 5}]MinLimit[(25 ^ x - 5 ^ x) / (4 ^ x - 2 ^ x), x -> 0]//SimplifyPlot[(25 ^ x - 5 ^ x) / (4 ^ x - 2 ^ x), {x, -1, 1}, PlotRange -> {-5, 5}]MinLimit[x ^ (1 / x), x -> ∞]Plot[{x ^ (1 / x), 1}, {x, 0, 40}, PlotRange -> All, PlotTheme -> "DashedLines"]//Quiet
MinLimit[x^n Exp[-1 / x^2], x -> 0, Assumptions -> n∈ℤ]これとは逆に，
はどの 
のベキ乗よりも速く発散するが，積の符号は 
の偶奇性に依存する：
MinLimit[x^n Exp[1 / x^2], x -> 0, Assumptions -> Mod[n, 2] == 0]MinLimit[x^n Exp[1 / x^2], x -> 0, Assumptions -> Mod[n, 2] == 1]Plot[{x^7 Exp[x^-2], x^6 Exp[x^-2], x^-7 Exp[-x^-2]}, {x, -1, 1}, PlotRange -> {-5, 5}, PlotTheme -> "DashedLines"]MinLimit[Log[x ^ 2] / x, x -> 0]Plot[Log[x ^ 2] / x, {x, -1, 1}, ExclusionsStyle -> Directive[StandardMagenta, Thick, Dashed]]MinLimit[x Log[x ^ 2], x -> 0]Plot[Log[x ^ 2]x, {x, -1, 1}]MinLimit[Log[x] / Sqrt[2x], x -> ∞]Plot[{Log[x] / Sqrt[2x], 0}, {x, 0, 1000}, PlotTheme -> "DashedLines", PlotRange -> 1]区分関数 (5)
f[x_] := Piecewise[{{2 / 5, x == 1}}, (x - 1) / (x ^ 2 - 1)]MinLimit[f[x], x -> 1]f[1]Plot[f[x], {x, 0, 2}, Epilog -> {PointSize[Medium], Point[{1, f[1]}]}]g[x_] := Piecewise[{{1 - x ^ 2, x ≤ 0}}, x ^ 2]MinLimit[g[x], x -> 0, Direction -> "FromAbove"]MinLimit[g[x], x -> 0, Direction -> "FromBelow"]MinLimit[g[x], x -> 0]Plot[g[x], {x, -1, 1}, Epilog -> {PointSize[Medium], Point[{0, g[0]}]}]UnitStepは，事実上，右連続区分関数である：
MinLimit[UnitStep[x], x -> 0, Direction -> "FromBelow"]MinLimit[UnitStep[x], x -> 0, Direction -> "FromAbove"]MinLimit[UnitStep[x], x -> 0]Plot[UnitStep[x], {x, -1, 1}, Epilog -> {ColorData["DefaultPlotColors"][1], PointSize[Large], Point[{0, UnitStep[0]}]}]RealSignは，事実上，不連続区分関数である：
MinLimit[RealSign[x], x -> 0, Direction -> "FromBelow"]MinLimit[RealSign[x], x -> 0, Direction -> "FromAbove"]MinLimit[RealSign[x], x -> 0]![TemplateBox[{0}, RealSign]](Files/MinLimit.ja/73.png "TemplateBox[{0}, RealSign]"){kind=small}
RealSign[0]Plot[RealSign[x], {x, -1, 1}, Epilog -> {ColorData["DefaultPlotColors"][1], PointSize[Medium], Point[{0, RealSign[0]}]}]x が整数値に近付くときのFloorの最小極限を求める：
MinLimit[Floor[x], x -> n, Assumptions -> n∈Integers]Plot[Floor[x], {x, -4, 4}, ExclusionsStyle -> Dashed]特殊関数 (4)
Gammaを含む最小極限：
MinLimit[Gamma[z], z -> -1]MinLimit[Sin[x]Gamma[x + 1] ^ (1 / x) / x, x -> ∞]Plot[{Sin[x]Gamma[x + 1] ^ (1 / x) / x, -1 / E}, {x, 0, 30}, PlotTheme -> "DashedLines"]MinLimit[BesselK[1, 3x], x -> 0, Direction -> -1]Plot[BesselK[1, 3x], {x, 0, 1}, PlotRange -> {0, 20}]MinLimit[x SphericalBesselJ[1, 2x], x -> ∞]Plot[{x SphericalBesselJ[1, 2x], -1 / 2}, {x, 0, 10}, PlotTheme -> "DashedLines"]MinLimit[SquareWave[x]FresnelS[x] / x ^ 3//PiecewiseExpand, x -> 0]Plot[{SquareWave[x]FresnelS[x] / x ^ 3, -Pi / 6}, {x, -2, 2}, PlotTheme -> "DashedLines", ExclusionsStyle -> Directive[StandardMagenta, Dashed]]MinLimit[Cos[x]Erfc[x], x -> -∞]Plot[{Cos[x]Erfc[x], -2}, {x, -28, 2}, PlotStyle -> {Automatic, Dashed}]非正の各偶数で，Gammaは片側から
に発散する：
MinLimit[Gamma[z], z -> a, Direction -> Reals, Assumptions -> a∈ℤ && a ≤ 0 && Mod[a, 2] == 0]MinLimit[Gamma[z], z -> a, Direction -> Reals, Assumptions -> a∈ℤ && a ≤ 0 && Mod[a, 2] == 1]ネストした最小極限 (3)
MinLimit[ArcTan[y / x], {y -> ∞, x -> ∞}]2つのMinLimit式を計算しても同じ結果が得られる：
MinLimit[MinLimit[ArcTan[y / x], x -> ∞], y -> ∞]
MinLimit[ArcTan[y / x], {x -> ∞, y -> ∞}]MinLimit[MinLimit[ArcTan[y / x], y -> ∞], x -> ∞]
MinLimit[Exp[(2y x/Sqrt[1 + y^2x^2 ])], {y -> -∞, x -> 0}]
MinLimit[Exp[(2y x/Sqrt[1 + y^2x^2 ])], {x -> 0, y -> -∞}]f[x_, y_] := (y /x + y )
MinLimit[f[x, y], {y -> 0, x -> 0}]
MinLimit[f[x, y], {x -> 0, y -> 0}]
がほとんど 
と相殺し合う点で任意に小さい値が与えられるので，真の二変量最大極限は
である：
MinLimit[f[x, y], {x, y} -> {0, 0}]
Limit[f[y^2 - y, y], y -> 0, Direction -> "FromBelow"]Show[Plot3D[f[x, y], {x, y}∈Disk[{0, 0}, 2], ClippingStyle -> None, Mesh -> None, BoxRatios -> 1], ParametricPlot3D[{{t, 0, f[t, 0]}, None, {0, t, f[0, t]}}, {t, -2, 2}, PlotStyle -> Thickness[0.025], PlotLegends -> LineLegend[{y == 0, None, x == 0}]], ViewPoint -> {-3, 1, 1}]多変量最小極限 (4)
f[x_, y_] := ArcTan[y ^ 2 / (x ^ 2 + x ^ 3)]MinLimit[f[x, y], {x -> 0, y -> 0}]MinLimit[f[x, y], {y -> 0, x -> 0}]
MinLimit[f[x, x], x -> 0]MinLimit[f[x, -x], x -> 0]
MinLimit[f[x, y], {x, y} -> {0, 0}]Show[Plot3D[f[x, y], {x, -1, 1}, {y, -1, 1}, Mesh -> None], ParametricPlot3D[{{t^2, t, f[t^2, t]}, None, {t, 0, f[t, 0]}}, {t, -1, 1}, PlotStyle -> Tube[0.05]]]f[x_, y_] := Tanh[(x + y/x - y)]
MinLimit[Tanh[(x + y/x - y)], {x, y} -> {0, 0}]MinLimit[f[x, y], {y -> 0, x -> 0}]MinLimit[Tanh[(x + y/x - y)], {x -> 0, y -> 0}]
f[x, m x]//Simplify最小値には，
のような 
が 
に近付く曲線に沿って達することができる：
Limit[f[x, xSqrt[1 + x^2]], x -> 0]Show[Plot3D[f[x, y], {x, -1, 1}, {y, -1, 1}, Mesh -> None], ParametricPlot3D[{{t, t Sqrt[1 + t^2], f[t, t Sqrt[1 + t^2]]}, {t, 0, f[t, 0]}, {0, t, f[0, t]}}, {t, -1, 1}, PlotStyle -> Thickness[0.025], PlotLegends -> LineLegend[{y == x Sqrt[1 - x ^ 2], y == 0, x == 0}]], BoxRatios -> Automatic]//Quietf[x_, y_] := (1 + x y)Sin[1 / (x ^ 2 + y ^ 2)]
MinLimit[f[x, y], {x, y} -> {0, 0}]//Quiet{x[r_, θ_], y[r_, θ_]} := {r Cos[θ], r Sin[θ]};Simplify[f[x[r, θ], y[r, θ]]]極表現は有界で，
で消失し，Sinの最小極限を残す：
MinLimit[f[x[r, θ], y[r, θ]], r -> 0, Direction -> -1]ParametricPlot3D[{x[r, θ], y[r, θ], f[x[r, θ], y[r, θ]]}, {r, 0, 1}, {θ, 0, 2Pi}, PlotStyle -> Opacity[.5]]f[x_, y_, z_] := (x z/x^2 + y^2 + z^2)
MinLimit[f[x, y, z], {x, y, z} -> {0, 0, 0}]{MinLimit[f[x, y, z], {x -> 0, y -> 0, z -> 0}], MinLimit[f[x, y, z], {y -> 0, z -> 0, x -> 0}], MinLimit[f[x, y, z], {z -> 0, x -> 0, y -> 0}]}
Limit[f[x, 0, -x], x -> 0]TransformedField["Cartesian" -> "Spherical", f[x, y, z], {x, y, z} -> {r, θ, φ}]//TrigExpandMinimize[Cos[θ] Cos[φ] Sin[θ], {θ, φ}∈Rectangle[{0, -Pi}, {Pi, Pi}]]//FullSimplify//QuietSliceContourPlot3D[f[x, y, z], {x, y, z}∈Ball[]]オプション (10)
Assumptions (1)
Assumptionsを使ってパラメータについての条件を指定する：
MinLimit[Sin[x]Exp[a x], x -> ∞, Assumptions -> a < 0]MinLimit[Sin[x]Exp[a x], x -> ∞, Assumptions -> a == 0]MinLimit[Sin[x]Exp[a x], x -> ∞, Assumptions -> a > 0]Direction (5)
MinLimit[1 / x, x -> 0, Direction -> "FromBelow"]MinLimit[1 / x, x -> 0, Direction -> 1]MinLimit[1 / x, x -> 0, Direction -> "FromAbove"]MinLimit[1 / x, x -> 0, Direction -> -1]デフォルトの方向はRealsである：
MinLimit[1 / x, x -> 0]MinLimit[1 / x, x -> 0, Direction -> Reals]"TwoSided"はRealsに等しい：
MinLimit[1 / x, x -> 0, Direction -> "TwoSided"]MinLimit[Re[(1/x^2)], x -> 0, Direction -> ℂ]MinLimit[Re[(1/x^2)], x -> 0]MinLimit[Im[EllipticK[2 + x]], x -> 0, Direction -> +I]MinLimit[Im[EllipticK[2 + x]], x -> 0, Direction -> Reals]MinLimit[Im[EllipticK[2 + x]], x -> 0, Direction -> -I]f[x_, y_] := (x y/x + y)(2 + RealSign[ x y] + RealSign[y])MinLimit[f[x, y], {x, y} -> {0, 0}, Direction -> "FromAbove"]MinLimit[f[x, y], {x, y} -> {0, 0}, Direction -> {"FromAbove", "FromAbove"}]MinLimit[f[x, y], {x, y} -> {0, 0}, Direction -> {"FromBelow", "FromAbove"}]MinLimit[f[x, y], {x, y} -> {0, 0}, Direction -> {"FromBelow", Reals}]//QuietMinLimit[f[x, y], {x, y} -> {0, 0}, Direction -> {Reals, "FromBelow"}]Row@{Plot3D[f[x, y], {x, y}∈Disk[], Exclusions -> {{x == -y , x <= 0}}, ClippingStyle -> None, ImageSize -> 200], DensityPlot[f[x, y], {x, -1, 1}, {y, -1, 1}, Exclusions -> {{x == -y , x <= 0}}, ClippingStyle -> Automatic, ImageSize -> Small]}GenerateConditions (3)
MinLimit[Sin[x]x ^ n, x -> ∞, GenerateConditions -> False]MinLimit[Sin[x]x ^ n, x -> ∞]MinLimit[Cos[x]Exp[a x], x -> ∞, GenerateConditions -> None]デフォルトで，一意的な結果が返されるような条件が生成される：
MinLimit[Cos[x]Exp[a x], x -> ∞]デフォルトで，特別な値が結果を無効にする場合にのみ条件は生成されない：
MinLimit[(x y/(x - a)^2 + y^2), {x, y} -> {0, 0}]GenerateConditions->Trueのときは，これらの一般的ではない条件さえも報告される：
MinLimit[(x y/(x - a)^2 + y^2), {x, y} -> {0, 0}, GenerateConditions -> True]PerformanceGoal (1)
PerformanceGoalを使って，高くつく可能性がある計算を回避する：
expr = (2 y z^2 - z^3 + y (x - 2 y + 3 z)^2 - z (x - 2 y + 3 z)^2/y^2 - 2 y z + z^2 - y (x - 2 y + 3 z) + z (x - 2 y + 3 z) + (x - 2 y + 3 z)^2);MinLimit[expr, {x, y, z} -> {0, 0, 0}, PerformanceGoal -> "Speed"]デフォルト設定では，使用可能なすべてのテクニックを使って結果を出そうとする：
MinLimit[expr, {x, y, z} -> {0, 0, 0}]アプリケーション (12)
最小極限の幾何学 (3)
f[x_] := Cos[Log[RealAbs[x]]] + Sin[x]MinLimit[f[x], x -> 0]このことは，
のときに 
である数列 
（例えば 
)がなければならないことを意味する：
x[n_] := Exp[-(2n + 1) Pi]
TableForm[N[Table[{x[n], f[x[n]]}, {n, 1, 5}], 10], TableHeadings -> {{}, {Subscript[x, n], HoldForm@f[Subscript[x, n]]}}]DiscreteLimit[x[n], n -> ∞]DiscreteLimit[f[x[n]], n -> ∞]この数列は，
それ自身が 
のときに極限を持たなくても存在する点に注意のこと：
Limit[f[x], x -> 0]
g[x_] := Cos[x]Sin[Tan[x]]Limit[g[x], x -> Pi / 2]MinLimit[g[x], x -> Pi / 2]
の周りの徐々に小さくなる領域では，
は徐々に平らになりグラフの中で 
の上になる部分が多くなる：
Manipulate[Plot[{g[x], 0}, {x, Pi / 2 - a, Pi / 2 + a}, PlotRange -> {-.5, 1}, PlotTheme -> "DashedLines"], {a, 1, 0.001}, SaveDefinitions -> True]
f[x_] := Sin[Tan[x]] + (x - Pi / 2)Limit[f[x], x -> Pi / 2]
MinLimit[f[x], x -> Pi / 2]
の周りの徐々に小さくなる領域では，
は激しく振動するが，
はどんどんそのよい床になる：
Manipulate[Plot[{f[x], -1}, {x, Pi / 2 - a, Pi / 2 + a}, PlotTheme -> "DashedLines"], {a, 1, 0.001}, SaveDefinitions -> True]漸近線の解析 (2)
![_(x->_(TemplateBox[{}, Reals])a)TemplateBox[{{{(, {f, (, x, )}, )}, /, {(, {g, (, x, )}, )}}}, Abs]>0](Files/MinLimit.ja/74.png "_(x->_(TemplateBox[{}, Reals])a)TemplateBox[{{{(, {f, (, x, )}, )}, /, {(, {g, (, x, )}, )}}}, Abs]>0"){kind=small}
のとき，関数 
は a における「big-omega of 
」（
と書く）と言われる：
Ω[x_, a_][f_, g_] := Underscript[, xUnderscript[ -> , ℝ]a]Abs[(f/g)] > 0
Ω[x, 0][Sin[x], x]
Ω[x, 0][Sin[x], Log[x]]
Ω[x, a][f[x], f[x]]
f[x_] := 3x + 2x ^ 2
g[x_] := x ^ 2 + 4x ^ 3
h[x_] := 4x ^ 3 + x ^ 4
{Ω[x, 0][f[x], g[x]], Ω[x, 0][g[x], h[x]], Ω[x, 0][f[x], h[x]]}f[x_] := Piecewise[{{-x, x <= 0}, {1/x, True}}]{Ω[x, 0][1, f[x]], Ω[x, 0][f[x], 1]}
funs = {x ^ 2, 1, x, x Log[x], Sin[x]};
Sort[funs, Ω[x, 0]]DSolveValue[m x''[t] + k x[t] == α Sin[Sqrt[k / m]t], x[t], t, Assumptions -> k > 0 && m > 0]MinLimit[%, t -> ∞, Assumptions -> k > 0 && m > 0]DSolveValue[m x''[t] + β x'[t] + k x[t] == α Sin[Sqrt[k / m]t], x[t], t, Assumptions -> k > 0 && m > 0 && β > 0 && β ^ 2 > 4 k m]振動動作は有界で，徐々に![+/-(TemplateBox[{alpha}, RealAbs])/betasqrt(k/m)](Files/MinLimit.ja/75.png "+/-(TemplateBox[{alpha}, RealAbs])/betasqrt(k/m)"){kind=small}
に制限される．これは安定性を示している：
MinLimit[%, t -> ∞, Assumptions -> k > 0 && m > 0 && β > 0 && β ^ 2 > 4k m]MaxLimit[%%, t -> ∞, Assumptions -> k > 0 && m > 0 && β > 0 && β ^ 2 > 4k m]連続性 (4)
![TemplateBox[{{f, (, x, )}, x, a}, MinLimit2Arg]>=f(a)](Files/MinLimit.ja/76.png "TemplateBox[{{f, (, x, )}, x, a}, MinLimit2Arg]>=f(a)"){kind=small}
なら，関数は 
において下半連続である．SawtoothWaveは
において上半連続である：
MinLimit[SawtoothWave[x], x -> 0] ≥ SawtoothWave[0]Plot[SawtoothWave[x], {x, -1, 1}, PlotStyle -> Thick, Epilog -> {ColorData["DefaultPlotColors"][1], PointSize[Large], Point[{0, SawtoothWave[0]}]}]一方，RealSignは原点において下半連続ではない：
MinLimit[RealSign[x], x -> 0] ≥ RealSign[0]Plot[RealSign[x], {x, -1, 1}, PlotStyle -> Thick, Epilog -> {ColorData["DefaultPlotColors"][1], PointSize[Large], Point[{0, RealSign[0]}]}]f[x_] := Piecewise[{{Sin[1/x], x > 0 || x < 0}, {-1, x == 0}}]MinLimit[f[x], x -> 0] ≥ f[0]これは，fが原点で左側極限も右側極限も持たないにもかかわらず，である：
{Underscript[, x -> 0^ + ]f[x], Underscript[, x -> 0^ - ]f[x]}fのMinLimitは0におけるfの値に依存しないので，
未満の任意の値でもf が下半連続になる点に注意のこと：
MinLimit[Piecewise[{{Sin[1/x], x > 0 || x < 0}, {a, x == 0}}], x -> 0]Plot[f[x], {x, -1, 1}, Epilog -> {ColorData["DefaultPlotColors"][2], PointSize[Large], Point[{0, f[0]}]}]![TemplateBox[{{f, (, x, )}, x, a}, MinLimit2Arg]>=f(a)](Files/MinLimit.ja/77.png "TemplateBox[{{f, (, x, )}, x, a}, MinLimit2Arg]>=f(a)"){kind=small}
(![TemplateBox[{{f, (, x, )}, x, a}, MaxLimit2Arg]<=f(a)](Files/MinLimit.ja/78.png "TemplateBox[{{f, (, x, )}, x, a}, MaxLimit2Arg]<=f(a)"){kind=small}
)なら，関数は 
において下（あるいは上）半連続である．実数値関数は，上半連続かつ下半連続のときかつそのときに限り連続関数である．SawtoothWaveは
において下半連続である：
MinLimit[SawtoothWave[x], x -> 0] ≥ SawtoothWave[0]MaxLimit[SawtoothWave[x], x -> 0] ≤ SawtoothWave[0]一方，以下はTriangleWaveが原点で連続であることを示している：
Underscript[, x -> 0]TriangleWave[x] ≤ TriangleWave[0] && Underscript[, x -> 0]TriangleWave[x] ≥ TriangleWave[0]GraphicsRow[Plot[#[x], {x, -1.5, 1.5}, IconizedObject[«Plot options»]]& /@ {SawtoothWave, TriangleWave}, ImageSize -> Medium]Ceilingは不連続であるがすべての整数において下半連続である：
Table[MinLimit[Ceiling[x], x -> k] ≥ Ceiling[k], {k, -5, 5}]一方，Floorは連続でもすべての整数において下半連続でもない：
Table[MinLimit[Floor[x], x -> k] ≥ Floor[k], {k, -5, 5}]どちらも非整数値では連続であるが，Ceilingだけがすべての
について下半連続である：
GraphicsRow[{Plot[Floor[x], {x, -5, 5}, IconizedObject[«Plot options»]], Plot[Ceiling[x], {x, -5, 5}, IconizedObject[«Plot options»]]}, ImageSize -> Medium]微分 (3)
diniLL[f_, x_] := Underscript[, h -> 0^ - ]DifferenceQuotient[f, {x, h}]
diniRL[f_, x_] := Underscript[, h -> 0^ + ]DifferenceQuotient[f, {x, h}]Rampは実線全体の上に有限下ディニ微分を持つ：
diniLL[Ramp[x], x]diniRL[Ramp[x], x]これらの2つの微分は原点以外あらゆるところで等しいことに注意のこと：
Simplify[% == %%]これは，Rampは原点以外のあらゆるところで微分可能であることを反映している：
Ramp'[x]Plot[{Ramp[x], Ramp'[x]}, {x, -2, 2}, PlotTheme -> "DashedLines"]f[x_] := Piecewise[{{x*Cos[1/x], x != 0}, {0, True}}]{f[0], Underscript[, xUnderscript[ -> , ℝ]0]f[x]}{Underscript[, h -> 0^ + ](f[h] - f[0]/h), Underscript[, h -> 0^ + ](f[h] - f[0]/h)}{Underscript[, h -> 0^ + ](f[h] - f[0]/h), Underscript[, h -> 0^ + ](f[h] - f[0]/h)}このことは，0の周りの関数の減少が有界であることを示している：
Plot[{f[x], -RealAbs[x]}, {x, -1, 1}, PlotTheme -> "DashedLines", Filling -> {1 -> {2}}]左ディニ微分は2つある．最初のものは左下ディニ微分 
で，次のように定義される：
diniLL[f_, x_] := Underscript[, h -> 0^ - ]DifferenceQuotient[f, {x, h}]
diniLU[f_, x_] := Underscript[, h -> 0^ - ]DifferenceQuotient[f, {x, h}]
は，
におけるRampと同じように，2つが等しく有限であるときかつそのときに限り，
で左微分可能である：
{diniLL[Ramp[x], x], diniLU[Ramp[x], x] } /. x -> 0
g[x_] := Piecewise[{{x*Cos[Cot[x]], x != 0}, {0, True}}]{diniLL[g[x], x], diniLU[g[x], x] } /. x -> 0Plot[{Ramp[x], g[x]}, {x, -.1, .1}, PlotTheme -> "DashedLines"]特性と関係 (13)
MinLimit[x Sin[x], x -> ∞]Limit[x Sin[x], x -> ∞]f[x_] := Sin[x]c = 3;MinLimit[c f[x], x -> a] == c MinLimit[f[x], x -> a]
![TemplateBox[{{(, {f, +, g}, )}, x, a}, MinLimit2Arg]>=TemplateBox[{f, x, a}, MinLimit2Arg]+TemplateBox[{g, x, a}, MinLimit2Arg]](Files/MinLimit.ja/82.png "TemplateBox[{{(, {f, +, g}, )}, x, a}, MinLimit2Arg]>=TemplateBox[{f, x, a}, MinLimit2Arg]+TemplateBox[{g, x, a}, MinLimit2Arg]"){kind=small}
f[x_] := Sin[x]g[x_] := Cos[x]MinLimit[f[x] + g[x], x -> ∞] ≥ MinLimit[f[x], x -> ∞] + MinLimit[g[x], x -> ∞]MinLimit[f[x] + g[x], x -> ∞] > MinLimit[f[x], x -> ∞] + MinLimit[g[x], x -> ∞]Assumptionsは最小極限式でパラメータに適用される：
MinLimit[Tan[x], x -> π / 2 + n π, Direction -> "FromAbove", Assumptions -> n∈Integers]Directionは極限変数に条件を置く：
MinLimit[Tan[x], x -> π / 2 + n π, Direction -> "FromBelow", Assumptions -> n∈Integers]Plot[Tan[x], {x, -2π, 2π}, ExclusionsStyle -> {{Dashed, StandardMagenta}}]ネストした最小極限を計算するときは，適切な仮定が後ろの極限変数に対して生成される：
MinLimit[ArcTan[y / x], {y -> 0, x -> 0}, Direction -> 1]MinLimit[ArcTan[y / x], x -> 0, Direction -> 1]MinLimit[ArcTan[y / x], x -> 0, Direction -> 1, Assumptions -> y < 0]実数値関数については，Limitが存在するならMinLimitは同じ値を持つ：
f[x_] := Sin[x] / xLimit[f[x], x -> ∞]MinLimit[f[x], x -> ∞]
![TemplateBox[{{(, {f, +, g}, )}, x, a}, MinLimit2Arg]=TemplateBox[{f, x, a}, MinLimit2Arg]+TemplateBox[{g, x, a}, MinLimit2Arg]](Files/MinLimit.ja/83.png "TemplateBox[{{(, {f, +, g}, )}, x, a}, MinLimit2Arg]=TemplateBox[{f, x, a}, MinLimit2Arg]+TemplateBox[{g, x, a}, MinLimit2Arg]"){kind=small}
f[x_] := x / (x + 1)g[x_] := Cos[x]Limit[f[x], x -> ∞]MinLimit[f[x] + g[x], x -> ∞] == MinLimit[f[x], x -> ∞] + MinLimit[g[x], x -> ∞]MinLimit[SquareWave[x], x -> ∞] ≤ MaxLimit[SquareWave[x], x -> ∞]MinLimitとMaxLimitが等しいときは，共通値に等しい極限が存在する：
f[x_] := Piecewise[{{1 + x, x <= 0}, {(x - 1)^2, True}}]{Underscript[, x -> 0]f[x], Underscript[, x -> 0]f[x], Underscript[, x -> 0]f[x]}
{MinLimit[x, x -> ∞], MaxLimit[x, x -> ∞], Limit[x, x -> ∞]}MinLimitは-MaxLimit[-f,…]として計算することができる：
f[x_] := Piecewise[{{2, x > 0}, {-1, True}}]MinLimit[f[x], x -> 0] == -MaxLimit[-f[x], x -> 0]
![TemplateBox[{{g, (, x, )}, x, a}, MinLimit2Arg]>=TemplateBox[{{f, (, x, )}, x, a}, MaxLimit2Arg]>=TemplateBox[{{f, (, x, )}, x, a}, MinLimit2Arg]](Files/MinLimit.ja/84.png "TemplateBox[{{g, (, x, )}, x, a}, MinLimit2Arg]>=TemplateBox[{{f, (, x, )}, x, a}, MaxLimit2Arg]>=TemplateBox[{{f, (, x, )}, x, a}, MinLimit2Arg]"){kind=small}
f[x_] := x Sin[1 / x]g[x_] := RealAbs[x]Reduce[f[x] ≤ g[x]]//SimplifyUnderscript[, xUnderscript[ -> , ℝ]0]g[x] ≥ Underscript[, xUnderscript[ -> , ℝ]0]f[x] ≥ Underscript[, xUnderscript[ -> , ℝ]0]f[x]例のように2つの最小極限が等しいとき，f は 
のとき極限を持つ：
Underscript[, xUnderscript[ -> , ℝ]0]f[x] == Underscript[, xUnderscript[ -> , ℝ]0]g[x] == Underscript[, xUnderscript[ -> , ℝ]0]f[x]これは，はさみうちの定理 （またはサンドイッチ定理）の一般化である：
Plot[{f[x], g[x]}, {x, -1, 1}, Filling -> {2 -> {1}}]MinLimitは常にDiscreteMinLimit以下である：
g[n_] := Sin[n π + Pi / 4]DiscreteMinLimit[g[n], n -> ∞]MinLimit[g[n], n -> ∞]Show[Plot[{g[n], -1, -1 / Sqrt[2]}, {n, 0, 10}, PlotTheme -> "DashedLines"], DiscretePlot[g[n], {n, 0, 10}, PlotMarkers -> {"Point", Medium}]]考えられる問題 (1)
おもしろい例題 (1)
f[x_] := {1 / x ^ 2, Sin[8x] / (6x), 3x ^ 4 / (x ^ 4 + 4), E ^ x, Sin[30 / x], x ^ 2Cos[4x ^ 2] / (x ^ 2 + 1)}a = {0, ∞, ∞, ∞, 0, ∞};range = {{0, 5}, {-0.5, 1.5}, {-2, 4}, {0, 25}, {-2, 2}, {-2, 2}};asym = {6Sign[x + 0.05], 0.02, 3, 0, {-1, 1}, {-1, 1}};Grid[Partition[Table[With[{r1 = f[x][[n]], r2 = a[[n]], r3 = range[[n]], r4 = asym[[n]]},
Plot[{r1, r4}, {x, -4, 4}, PlotRange -> r3, ImageSize -> 210, PlotStyle -> {Automatic, {ThemeColor["Foreground"], Dashed}, {ThemeColor["Foreground"], Dashed}}, ExclusionsStyle -> {{ThemeColor["Foreground"], Dashed}}, PlotLabel -> Style[HoldForm[MinLimit[r1, x -> r2, Direction -> Reals]] == MinLimit[f[x][[n]], x -> r2], ScriptLevel -> 0]]], {n, 1, 6}], 2], Frame -> All]
Wolfram Research (2017), MinLimit, Wolfram言語関数， https://reference.wolfram.com/language/ref/MinLimit.html.
テキスト
Wolfram Research (2017), MinLimit, Wolfram言語関数， https://reference.wolfram.com/language/ref/MinLimit.html.
CMS
Wolfram Language. 2017. "MinLimit." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/MinLimit.html.
APA
Wolfram Language. (2017). MinLimit. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/MinLimit.html