



MinLimit
Details and Options

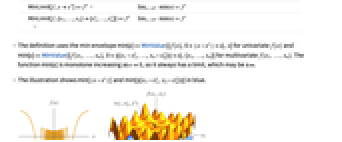


- MinLimit is also known as limit inferior, infimum limit, liminf, lower limit and inner limit.
- MinLimit computes the largest lower bound for the limit and is always defined for real-valued functions. It is often used to give conditions of convergence and other asymptotic properties where no actual limit is needed.
- By using the character , entered as
 mlim
mlim or \[MinLimit], with underscripts or subscripts, min limits can be entered as follows:
or \[MinLimit], with underscripts or subscripts, min limits can be entered as follows: -
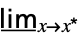 f
fmin limit in the default direction 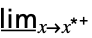 f
fmin limit from above 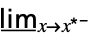 f
fmin limit from below 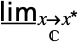 f
fmin limit in the complex plane 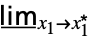 …
…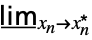 f
fMinLimit[f,{x1 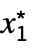 ,…,xn
,…,xn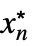 }]
}] - For a finite limit point x* and {
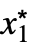 ,…,
,…,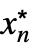 }:
}: -
MinLimit[f,xx*]f* ![TemplateBox[{{min, (, epsilon, )}, epsilon, 0, +, {Direction, ->, {-, 1}}}, LimitWithSuperscript, DisplayFunction -> ({Sequence[{Sequence["lim"], _, DocumentationBuild`Utils`Private`Parenth[{#2, ->, {#3, ^, DocumentationBuild`Utils`Private`Parenth[#4]}}, LimitsPositioning -> True]}], #1} & ), InterpretationFunction -> ({Limit, [, {#1, ,, {#2, ->, #3}, ,, #5}, ]} & )]=f^* TemplateBox[{{min, (, epsilon, )}, epsilon, 0, +, {Direction, ->, {-, 1}}}, LimitWithSuperscript, DisplayFunction -> ({Sequence[{Sequence["lim"], _, DocumentationBuild`Utils`Private`Parenth[{#2, ->, {#3, ^, DocumentationBuild`Utils`Private`Parenth[#4]}}, LimitsPositioning -> True]}], #1} & ), InterpretationFunction -> ({Limit, [, {#1, ,, {#2, ->, #3}, ,, #5}, ]} & )]=f^*](Files/MinLimit.en/24.png)
MinLimit[f,{x1,…,xn}{ 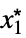 ,…,
,…,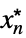 }]f*
}]f* ![TemplateBox[{{min, (, epsilon, )}, epsilon, 0, +, {Direction, ->, {-, 1}}}, LimitWithSuperscript, DisplayFunction -> ({Sequence[{Sequence["lim"], _, DocumentationBuild`Utils`Private`Parenth[{#2, ->, {#3, ^, DocumentationBuild`Utils`Private`Parenth[#4]}}, LimitsPositioning -> True]}], #1} & ), InterpretationFunction -> ({Limit, [, {#1, ,, {#2, ->, #3}, ,, #5}, ]} & )]=f^* TemplateBox[{{min, (, epsilon, )}, epsilon, 0, +, {Direction, ->, {-, 1}}}, LimitWithSuperscript, DisplayFunction -> ({Sequence[{Sequence["lim"], _, DocumentationBuild`Utils`Private`Parenth[{#2, ->, {#3, ^, DocumentationBuild`Utils`Private`Parenth[#4]}}, LimitsPositioning -> True]}], #1} & ), InterpretationFunction -> ({Limit, [, {#1, ,, {#2, ->, #3}, ,, #5}, ]} & )]=f^*](Files/MinLimit.en/27.png)
- The definition uses the min envelope min[ϵ]MinValue[{f[x],0<
![TemplateBox[{{x, -, {x, ^, *}}}, Abs] TemplateBox[{{x, -, {x, ^, *}}}, Abs]](Files/MinLimit.en/28.png) <ϵ},x] for univariate f[x] and min[ϵ]MinValue[{f[x1,…,xn],0<
<ϵ},x] for univariate f[x] and min[ϵ]MinValue[{f[x1,…,xn],0<![TemplateBox[{{{, {{{x, _, {(, 1, )}}, -, {x, _, {(, 1, )}, ^, *}}, ,, ..., ,, {{x, _, n}, -, {x, _, {(, n, )}, ^, *}}}, }}}, Norm] TemplateBox[{{{, {{{x, _, {(, 1, )}}, -, {x, _, {(, 1, )}, ^, *}}, ,, ..., ,, {{x, _, n}, -, {x, _, {(, n, )}, ^, *}}}, }}}, Norm]](Files/MinLimit.en/29.png) <ϵ},{x1,…,xn}] for multivariate f[x1,…,xn]. The function min[ϵ] is monotone increasing as ϵ0, so it always has a limit, which may be ±∞.
<ϵ},{x1,…,xn}] for multivariate f[x1,…,xn]. The function min[ϵ] is monotone increasing as ϵ0, so it always has a limit, which may be ±∞. - The illustration shows min[
![TemplateBox[{{x, -, {x, ^, *}}}, Abs] TemplateBox[{{x, -, {x, ^, *}}}, Abs]](Files/MinLimit.en/30.png) ] and min[
] and min[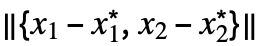 ] in blue.
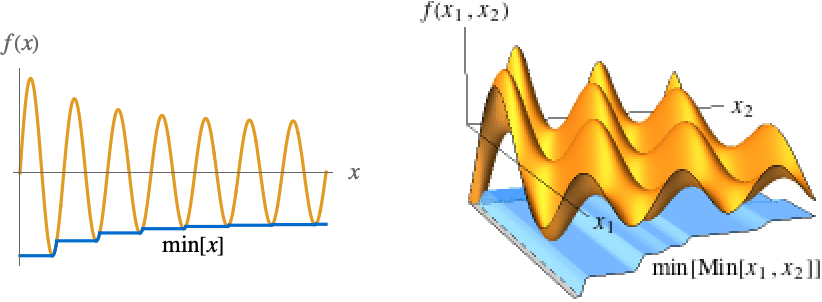
] in blue. - For an infinite limit point x*∞, the min envelope min[ω]MinValue[{f[x],x>ω},x] is used for univariate f[x] and min[ω]MinValue[{f[x1,…,xn],x1>ω∧⋯∧xn>ω},{x1,…,xn}] for multivariate f[x1,…,xn]. The function min[ω] is monotone increasing as ω∞, so it always has a limit.
- The illustration shows min[x] and min[Min[x1,x2]] in blue.
- MinLimit returns unevaluated when the min limit cannot be found.
- The following options can be given:
-
Assumptions $Assumptions assumptions on parameters Direction Reals directions to approach the limit point GenerateConditions Automatic whether to generate conditions on parameters Method Automatic method to use PerformanceGoal "Quality" aspects of performance to optimize - Possible settings for Direction include:
-
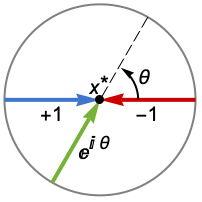
Reals or "TwoSided" from both real directions "FromAbove" or -1 from above or larger values "FromBelow" or +1 from below or smaller values Complexes from all complex directions Exp[ θ] in the direction 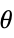
{dir1,…,dirn} use direction diri for variable xi independently - DirectionExp[ θ] at x* indicates the direction tangent of a curve approaching the limit point x*.
- Possible settings for GenerateConditions include:
-
Automatic non-generic conditions only True all conditions False no conditions None return unevaluated if conditions are needed - Possible settings for PerformanceGoal include $PerformanceGoal, "Quality" and "Speed". With the "Quality" setting, MinLimit typically solves more problems or produces simpler results, but it potentially uses more time and memory.
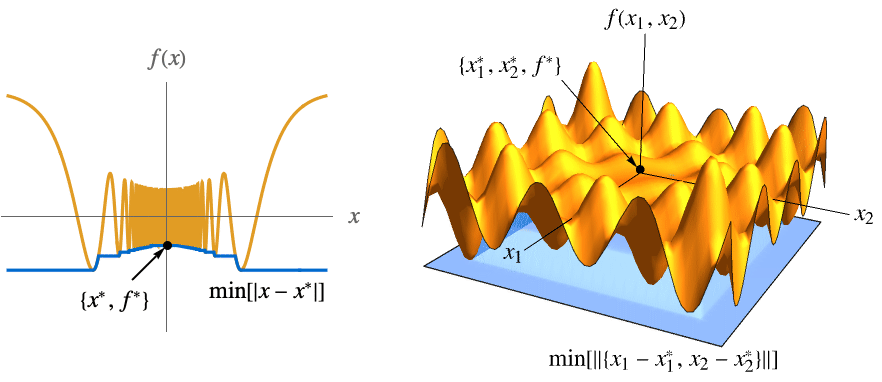
Examples
open all close allBasic Examples (3)
Scope (35)
Basic Uses (5)
Find the min limit at a point:
Find the min limit at a symbolic point:
Find the min limit at -Infinity:
The nested min limit as ![]() first and then
first and then ![]() :
:
Typeset Limits (4)
Use ![]() mlim
mlim![]() to enter the character, and
to enter the character, and ![]() to create an underscript:
to create an underscript:
Take a limit from above or below by using a superscript ![]() or
or ![]() on the limit point:
on the limit point:
After typing zero, use ![]() to create a superscript:
to create a superscript:
To specify a direction of Reals or Complexes, enter the domain as an underscript on the character:
Enter the rule as ![]() ->
->![]() , use
, use ![]() to create an underscript, and type
to create an underscript, and type ![]() reals
reals![]() to enter
to enter ![]() :
:
TraditionalForm formatting:
Elementary Functions (10)
Rational functions at singular points:
Rational functions at ±Infinity:
Trigonometric functions at singular points:
Trigonometric functions at ±Infinity:
Inverse trigonometric functions:
The function ![]() decays faster than any power of
decays faster than any power of ![]() as
as ![]() :
:
Conversely, ![]() blows up faster than any power of
blows up faster than any power of ![]() , but the sign of the product depends on the parity of
, but the sign of the product depends on the parity of ![]() :
:
Piecewise Functions (5)
A discontinuous piecewise function:
A left-continuous piecewise function:
The two-sided min limit is the smaller of the two:
UnitStep is effectively a right-continuous piecewise function:
RealSign is effectively a discontinuous piecewise function:
Note that ![]() is related to neither value:
is related to neither value:
Find the min limit of Floor as x approaches integer values:
Special Functions (4)
Nested Min Limits (3)
Compute the nested min limit as first ![]() and then
and then ![]() :
:
The same result is obtained by computing two MinLimit expressions:
Computing the min limit as first ![]() and then
and then ![]() yields a different answer:
yields a different answer:
This is again equivalent to two nested min limits:
The nested min limit as first ![]() and then
and then ![]() is
is ![]() :
:
The nested min limit as first ![]() and then
and then ![]() is
is ![]() :
:
Consider the function for two variables at the origin:
The iterated min limit as ![]() and then
and then ![]() is
is ![]() :
:
The iterated min limit as ![]() and then
and then ![]() is
is ![]() :
:
The true bivariate min limit is ![]() , as points where
, as points where ![]() almost cancels
almost cancels ![]() give arbitrarily small values:
give arbitrarily small values:
For example, this value can be approached along the curve ![]() :
:
Visualize the function and the values along the two axes computed previously:
Multivariate Min Limits (4)
Find the min limit of a multivariate function:
The two nested min limits give different answers:
Approaching the origin along the curves ![]() yields a third result:
yields a third result:
The true two-dimensional lower limit of the function is ![]() , achieved along the
, achieved along the ![]() axis:
axis:
Visualize the minimum and maximum values near the origin:
Find the min limit of a bivariate function:
The true two-dimensional min limit of the function is ![]() :
:
Note that neither iterated limit gives this result:
Indeed, along any rate ![]() , the function is constant:
, the function is constant:
The minimum is approached along curves with ![]() close to
close to ![]() , such as
, such as ![]() :
:
Visualize the function and the three min limits computed:
Find the min limit of a bivariate function at the origin:
The true two-dimensional min limit at the origin is ![]() :
:
Re-express the function in terms of polar coordinates:
The polar expression is bounded and disappears as ![]() , leaving the min limit of Sin:
, leaving the min limit of Sin:
Compute the min limit of a trivariate function:
The min limit at the origin is ![]() :
:
Note that the various iterated min limits are 0:
This is because the minimum is achieved along the line ![]() ,
, ![]() :
:
The min limit can also be understood by transforming to spherical coordinates:
Options (10)
Assumptions (1)
Specify conditions on parameters using Assumptions:
Direction (5)
The default direction is Reals:
"TwoSided" is equivalent to Reals:
Min limit in the complex plane:
Compare with the limit over the reals:
Compute the bivariate min limit approach from different quadrants:
Approaching the origin from the first quadrant:
Approaching the origin from the second quadrant:
Approaching the origin from the left half-plane:
GenerateConditions (3)
Return a result without stating conditions:
This result is only valid if n>0:
Return unevaluated if the results depend on the value of parameters:
By default, conditions are generated that return a unique result:
By default, conditions are not generated if only special values invalidate the result:
With GenerateConditions->True, even these non-generic conditions are reported:
PerformanceGoal (1)
Use PerformanceGoal to avoid potentially expensive computations:
The default setting uses all available techniques to try to produce a result:
Applications (12)
Geometry of Min Limits (3)
The function ![]() has a min limit of
has a min limit of ![]() at
at ![]() :
:
This means there must be a sequence ![]() for which
for which ![]() as
as ![]() ; for example,
; for example, ![]() :
:
Numerically, ![]() and
and ![]() quite quickly:
quite quickly:
Compute the two sequence limits exactly:
Note that this sequence exists even though ![]() itself does not have a limit as
itself does not have a limit as ![]() :
:
The function ![]() has the limit zero as
has the limit zero as ![]() approaches
approaches ![]() :
:
In increasingly small regions around ![]() ,
, ![]() gets increasingly flat, and more of the graph is above
gets increasingly flat, and more of the graph is above ![]() :
:
The function ![]() does not have a limit as
does not have a limit as ![]() approaches
approaches ![]() :
:
In increasingly small regions around ![]() ,
, ![]() bounces wildly, but
bounces wildly, but ![]() becomes a better and better floor for it:
becomes a better and better floor for it:
Asymptotic Analysis (2)
A function ![]() is said to be "big-omega of
is said to be "big-omega of ![]() " at a, written
" at a, written ![]() , if
, if ![]() :
:
It is possible for functions to share neither relationship:
Thus, ![]() is a reflexive partial order on functions:
is a reflexive partial order on functions:
![]() if
if ![]() goes to zero no faster than
goes to zero no faster than ![]() :
:
Find the motion of a critically driven mass-spring system:
The motion is oscillatory but becomes arbitrarily negative, indicating an instability:
The oscillatory motion is bounded and eventually restricted to ![]() , indicating stability:
, indicating stability:
Continuity (4)
A function is lower semicontinuous at t ![]() if
if ![]() . SawtoothWave is upper semicontinuous at
. SawtoothWave is upper semicontinuous at ![]() :
:
On the other hand, RealSign is not lower semicontinuous at the origin:
Consider the following function:
This function is lower semicontinuous at the origin:
This is despite f having neither a left nor a right limit at the origin:
Note that the MinLimit of f does not depend on the value of f at zero, so any value less than ![]() would also make f lower semicontinuous:
would also make f lower semicontinuous:
A function is upper semicontinuous at ![]() if
if ![]() . A real-valued function is continuous iff it is both upper and lower semicontinuous. UnitStep is upper semicontinuous at
. A real-valued function is continuous iff it is both upper and lower semicontinuous. UnitStep is upper semicontinuous at ![]() :
:
However, it is not upper semicontinuous, so it is discontinuous at the origin:
On the other hand, the following shows that TriangleWave is continuous at the origin:
Ceiling is discontinuous but lower semicontinuous at every integer:
On the other hand, Floor is neither continuous nor lower semicontinuous at the integers:
Both are continuous at noninteger values, but only Ceiling is lower semicontinuous on all of ![]() :
:
Differentiation (3)
The left-lower Dini derivative ![]() is defined as:
is defined as:
The right-lower Dini derivative ![]() is defined similarly:
is defined similarly:
Ramp has finite lower Dini derivatives on the whole real line:
Note that these two derivatives are equal everywhere except the origin:
This is a reflection of the fact that Ramp is differentiable everywhere except the origin:
Consider the following function:
It is continuous at the origin:
But it has neither a left nor a right derivative:
It does, however, have finite Dini derivatives:
This indicates that the decrease of the function around zero is bounded:
There are two left Dini derivatives. The first is the left-lower Dini derivative ![]() , defined as follows:
, defined as follows:
The right-lower Dini derivative ![]() is defined similarly using a max limit:
is defined similarly using a max limit:
![]() is left differentiable at
is left differentiable at ![]() if and only if the two are equal and finite, as in the case of Ramp at
if and only if the two are equal and finite, as in the case of Ramp at ![]() :
:
However, the function ![]() does not have a left derivative at the origin:
does not have a left derivative at the origin:
Properties & Relations (13)
A real-valued function always has a (possibly infinite) min limit:
The corresponding limit may not exist:
Positive multiplicative constants can be moved outside a min limit:
If ![]() and
and ![]() have finite min limits as
have finite min limits as ![]() , then
, then ![]() :
:
In this case, there is strict inequality:
Assumptions applies to parameters in the min limit expression:
Direction places conditions on the limit variable:
When computing nested min limits, appropriate assumptions are generated on later limit variables:
For a real-valued function, if Limit exists, then MinLimit has the same value:
If ![]() has a finite limit as
has a finite limit as ![]() , then
, then ![]() :
:
MinLimit is always less than or equal to MaxLimit:
If MinLimit and MaxLimit are equal, then the limit exists and equals their common value:
If the min limit is ![]() , then the max limit and thus the limit are also
, then the max limit and thus the limit are also ![]() :
:
MinLimit can be computed as -MaxLimit[-f,…]:
If the two min limits are equal—as in this example—then f has a limit as ![]() :
:
This is a generalization of the "squeezing" or "sandwich" theorem:
MinLimit is always less than or equal to DiscreteMinLimit:
Possible Issues (1)
MinLimit is only defined for real-valued functions:
Related Guides
History
Text
Wolfram Research (2017), MinLimit, Wolfram Language function, https://reference.wolfram.com/language/ref/MinLimit.html.
CMS
Wolfram Language. 2017. "MinLimit." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/MinLimit.html.
APA
Wolfram Language. (2017). MinLimit. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/MinLimit.html
BibTeX
@misc{reference.wolfram_2025_minlimit, author="Wolfram Research", title="{MinLimit}", year="2017", howpublished="\url{https://reference.wolfram.com/language/ref/MinLimit.html}", note=[Accessed: 07-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_minlimit, organization={Wolfram Research}, title={MinLimit}, year={2017}, url={https://reference.wolfram.com/language/ref/MinLimit.html}, note=[Accessed: 07-February-2026]}