MittagLefflerE

MittagLefflerE[α,z]

gives the Mittag–Leffler function TemplateBox[{alpha, z}, MittagLefflerE].

MittagLefflerE[α,β,z]

gives the generalized Mittag–Leffler function TemplateBox[{alpha, beta, z}, MittagLefflerE2].

Details

  • MittagLefflerE is a mathematical function, suitable for both symbolic and numerical manipulation.
  • MittagLefflerE is typically used in the solution of fractional-order differential equations, similar to the Exp function in the solution of ordinary differential equations.
  • MittagLefflerE allows 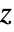alpha to be any real number.
  • The generalized Mittag–Leffler function is an entire function of 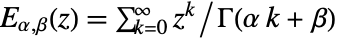given by its defining series TemplateBox[{alpha, beta, z}, MittagLefflerE2]=sum_(k=0)^inftyz^k/TemplateBox[{{{alpha, , k}, +, beta}}, Gamma].
  • The Mittag–Leffler function TemplateBox[{alpha, z}, MittagLefflerE] is equivalent to TemplateBox[{alpha, 1, z}, MittagLefflerE2].
  • MittagLefflerE automatically threads over lists. »

Examples

open allclose all

Basic Examples  (5)

Evaluate numerically:

Plot over a subset of the reals:

Plot over a subset of the complexes:

Series expansion at the origin:

Series expansion at Infinity:

Scope  (34)

Numerical Evaluation  (7)

Evaluate numerically:

Evaluate for negative values of alpha:

Evaluate to high precision:

The precision of the output tracks the precision of the input:

Complex number input:

Evaluate efficiently at high precision:

Compute the elementwise values of an array using automatic threading:

Or compute the matrix MittagLefflerE function using MatrixFunction:

Compute average-case statistical intervals using Around:

Specific Values  (5)

Simple exact values are generated automatically:

Evaluate symbolically:

For small integer values of and , MittagLefflerE can be expressed in terms of elementary functions:

Use FunctionExpand for other cases:

Values at infinity:

Find a value of x for which MittagLefflerE[1/2,x]=0.5:

Visualization  (3)

Plot the MittagLefflerE function for integer values of alpha:

Plot the MittagLefflerE function for noninteger values of alpha:

Plot the real part of TemplateBox[{2, z}, MittagLefflerE]:

Plot the imaginary part of TemplateBox[{2, z}, MittagLefflerE]:

Function Properties  (8)

TemplateBox[{a, x}, MittagLefflerE] is defined for all and real :

The complex domain of MittagLefflerE is the same:

MittagLefflerE has the mirror property TemplateBox[{1, {z, }}, MittagLefflerE]=TemplateBox[{1, z}, MittagLefflerE]:

MittagLefflerE threads elementwise over lists:

MittagLefflerE is an analytic function for :

It is singular and discontinuous for :

TemplateBox[{2, x}, MittagLefflerE] is injective:

TemplateBox[{{1, /, 2}, x}, MittagLefflerE] is not surjective:

TemplateBox[{{1, /, 2}, x}, MittagLefflerE] is non-negative:

TemplateBox[{{a, ,, 1}, x}, MittagLefflerE] simplifies to TemplateBox[{a, x}, MittagLefflerE]:

Differentiation  (3)

First derivatives with respect to z:

Higher derivatives with respect to z:

Plot the higher derivatives with respect to z when a=1/4:

Use FunctionExpand for derivatives with respect to parameters:

Integration  (2)

Indefinite integral of MittagLefflerE:

More integrals:

Series Expansions  (2)

Find the Taylor expansion using Series:

Plots of the first three approximations around :

Taylor expansion at a generic point:

Fractional Differential Equations  (3)

MittagLefflerE plays an important role in expressing solutions of fractional DEs with constant coefficients:

Verify the solution:

Plot the solution:

Solve a fractional DE with constant coefficients containing two Caputo derivatives of different orders:

Solve a system of two fractional DEs in vector form:

Plot the solution:

Parametrically plot the solution:

Integral Transforms  (1)

Laplace transform of specific MittagLefflerE functions:

ComplexPlot in the -domain:

Apply InverseLaplaceTransform to transform back to the time domain and get the initial expression:

Applications  (5)

The InverseLaplaceTransform of an algebraic function with fractional exponents can be expressed in terms of MittagLefflerE:

Define a Mittag–Leffler random variate for :

A Mittag–Leffler random variate is related to the positive stable random variate:

Generate random variates and compare the histogram to the distribution density:

A matrix and vector:

Define a function for computing the Krylov matrix from a given matrix and vector:

Compute the eigenvalues of the matrix:

Linear Caputo differential equations with constant coefficients can be solved using MittagLefflerE along with a Krylov matrix and the inverse of a Vandermonde matrix:

Verify that the same result can be obtained from DSolveValue:

Carlitz defines a -permutation as a permutation with consecutive runs of increasing elements, followed by a tail of increasing elements. The figure below illustrates the case , :

Generate all permutations of length 8:

Count the number of (3,2)-permutations of length 8:

Define the Olivier function:

The generating function for the number of -permutations can be expressed as a ratio of Olivier functions. Use the generating function to count the number of (3,2)-permutations of length 8:

The universal Kepler equation can be used to predict the position and velocity of an orbiting body at a given time from an initial time . Here are the heliocentric position and velocity vectors of Mars from a given initial time:

Compute the magnitudes of the position and velocity vectors:

Compute the initial radial velocity:

Compute the reciprocal of the semimajor axis from the vis-viva equation:

Estimate the position and velocity vectors of Mars after 8 hours have passed:

Define the Stumpff function, which appears in the universal variable formulation of the Kepler equation:

Solve for the "universal anomaly" from the universal Kepler equation:

Compute the Lagrange coefficients from the universal anomaly:

Compute the position vector after eight hours:

Compare with the true value:

Compute the derivative of the Lagrange coefficients with respect to time:

Compute the velocity vector after eight hours:

Compare with the true value:

Properties & Relations  (4)

The Mittag–Leffler function is closed under differentiation:

The TemplateBox[{a, x}, MittagLefflerE] function simplifies to elementary functions for small non-negative integer :

Larger non-negative integer values of give results in terms of HypergeometricPFQ:

For non-negative half-integer , TemplateBox[{a, x}, MittagLefflerE] simplifies to a sum of HypergeometricPFQ functions:

The defining sum for the Mittag–Leffler function:

For specific values of , this sum might be written in terms of HypergeometricPFQ functions:

Compare this with the MittagLefflerE output:

The family of MittagLefflerE functions can be represented in terms of FoxH:

Wolfram Research (2012), MittagLefflerE, Wolfram Language function, https://reference.wolfram.com/language/ref/MittagLefflerE.html (updated 2024).

Text

Wolfram Research (2012), MittagLefflerE, Wolfram Language function, https://reference.wolfram.com/language/ref/MittagLefflerE.html (updated 2024).

CMS

Wolfram Language. 2012. "MittagLefflerE." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2024. https://reference.wolfram.com/language/ref/MittagLefflerE.html.

APA

Wolfram Language. (2012). MittagLefflerE. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/MittagLefflerE.html

BibTeX

@misc{reference.wolfram_2024_mittaglefflere, author="Wolfram Research", title="{MittagLefflerE}", year="2024", howpublished="\url{https://reference.wolfram.com/language/ref/MittagLefflerE.html}", note=[Accessed: 16-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_mittaglefflere, organization={Wolfram Research}, title={MittagLefflerE}, year={2024}, url={https://reference.wolfram.com/language/ref/MittagLefflerE.html}, note=[Accessed: 16-November-2024 ]}