MittagLefflerE
MittagLefflerE[α,z]
Mittag–Leffler関数 ![]() を与える.
を与える.
MittagLefflerE[α,β,z]
一般化されたMittag–Leffler関数 ![]() を与える.
を与える.
詳細

- MittagLefflerEは記号操作・数値操作の両方に適した数学関数である.
- MittagLefflerEは,通常,常微分方程式の解におけるExpと同じように非整数階微分方程式の解で使われる.
- MittagLefflerEでは,
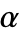 は任意の実数でよい.
は任意の実数でよい. - 一般化されたMittag–Leffler関数はその定義級数
![TemplateBox[{alpha, beta, z}, MittagLefflerE2]=sum_(k=0)^inftyz^k/TemplateBox[{{{alpha, , k}, +, beta}}, Gamma] TemplateBox[{alpha, beta, z}, MittagLefflerE2]=sum_(k=0)^inftyz^k/TemplateBox[{{{alpha, , k}, +, beta}}, Gamma]](Files/MittagLefflerE.ja/5.png) によって与えられる
によって与えられる 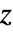 の整関数である.
の整関数である. - Mittag–Leffler関数
![TemplateBox[{alpha, z}, MittagLefflerE] TemplateBox[{alpha, z}, MittagLefflerE]](Files/MittagLefflerE.ja/7.png) は
は ![TemplateBox[{alpha, 1, z}, MittagLefflerE2] TemplateBox[{alpha, 1, z}, MittagLefflerE2]](Files/MittagLefflerE.ja/8.png) に等しい.
に等しい. - MittagLefflerEは自動的にリストに縫い込まれる. »
例題
すべて開くすべて閉じる例 (5)基本的な使用例
スコープ (34)標準的な使用例のスコープの概要
数値評価 (7)
MatrixFunctionを使って行列のMittagLefflerE関数を計算することもできる:
Aroundを使って平均的な場合の統計区間を計算する:
特定の値 (5)
MittagLefflerEは,![]() と
と ![]() の小さい整数値について初等関数で表すことができる:
の小さい整数値について初等関数で表すことができる:
その他の場合にはFunctionExpandを使う:
MittagLefflerE[1/2,x]=0.5となるような x の値を求める:
可視化 (3)
関数の特性 (8)
MittagLefflerEの複素領域も同じである:
MittagLefflerEは鏡特性 ![]() を持つ:
を持つ:
MittagLefflerEは要素単位でリストに縫い込まれる:
MittagLefflerEは ![]() のときは解析関数である:
のときは解析関数である:
微分 (3)
積分 (2)
級数展開 (2)
非整数階微分方程式 (3)
MittagLefflerEは定数係数を持つ非整数階偏微分方程式の解の表示において重要な役割を果たす:
積分変換 (1)
アプリケーション (5)この関数で解くことのできる問題の例
分数指数を持つ代数関数のInverseLaplaceTransformはMittagLefflerEで表すことができる:
Mittag–Leffler確率変量は正定値確率変量に関連している:
与えられた行列とベクトルからKrylov行列を計算する関数を定義する:
一定係数を持つ線形Caputo微分方程式はKrylov行列およびVandermonde行列の逆行列とともにMittagLefflerEを使って解くことができる:
DSolveValueを使っても同じ結果が得られることを確認する:
Carlitzは,![]() 順列を
順列を ![]() 個の増加要素が連続して続き,その後に
個の増加要素が連続して続き,その後に ![]() 個の増加要素が続く順列として定義した.以下の図は,
個の増加要素が続く順列として定義した.以下の図は,![]() ,
,![]() の場合を示している:
の場合を示している:

![]() 順列の数についての母関数はOlivier関数の比として表現できる.母関数を使って長さ8の(3,2)順列の数を数える:
順列の数についての母関数はOlivier関数の比として表現できる.母関数を使って長さ8の(3,2)順列の数を数える:
普遍ケプラー(Kepler)方程式を使って初期時点 ![]() からの時点
からの時点 ![]() における周回体の位置と速度が予測できる.次は,初期時点からの火星の太陽を中心とした位置と速度ベクトルである:
における周回体の位置と速度が予測できる.次は,初期時点からの火星の太陽を中心とした位置と速度ベクトルである:
ケプラー方程式の普遍式に出現するStumpff関数を定義する:
特性と関係 (4)この関数の特性および他の関数との関係
![]() のより大きい非負の整数値については,HypergeometricPFQによって結果が与えられる:
のより大きい非負の整数値については,HypergeometricPFQによって結果が与えられる:
非負の半整数 ![]() については,
については,![]() はHypergeometricPFQ関数の和に簡約される:
はHypergeometricPFQ関数の和に簡約される:
この和は ![]() の特定の値についてHypergeometricPFQ関数の観点から書かれているかもしれない:
の特定の値についてHypergeometricPFQ関数の観点から書かれているかもしれない:
これをMittagLefflerE出力と比較する:
MittagLefflerE関数族はFoxHによって表すことができる:
テキスト
Wolfram Research (2012), MittagLefflerE, Wolfram言語関数, https://reference.wolfram.com/language/ref/MittagLefflerE.html (2024年に更新).
CMS
Wolfram Language. 2012. "MittagLefflerE." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2024. https://reference.wolfram.com/language/ref/MittagLefflerE.html.
APA
Wolfram Language. (2012). MittagLefflerE. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/MittagLefflerE.html