Enable JavaScript to interact with content and submit forms on Wolfram websites. Learn how

MittagLefflerE

MittagLefflerE[α,z]

给出 Mittag–Leffler 函数 .

MittagLefflerE[α,β,z]

给出广义 Mittag–Leffler 函数 .

更多信息

MittagLefflerE 是一个数学函数，适宜于符号和数值运算.
MittagLefflerE 通常在分数阶微分方程的解中被使用，类似于常微分方程的解中的 Exp 函数.
MittagLefflerE 允许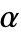是任意实数.
广义 Mittag–Leffler 函数是关于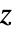的整函数，由定义级数 $TemplateBox[{alpha, beta, z}, MittagLefflerE2]=sum_(k=0)^inftyz^k/TemplateBox[{{{alpha, , k}, +, beta}}, Gamma]$ 给出.
Mittag–Leffler 函数等价于 .
MittagLefflerE 自动逐项作用于列表的各个元素. »

范例

打开所有单元关闭所有单元

基本范例 (5)

数值化计算：

在实数的子集上绘图：

在复数的子集上绘图：

在原点的级数展开：

在 Infinity 的级数展开：

范围 (34)

数值计算 (7)

数值化计算：

对的负值进行评估：

高精度计算：

输出的精度与输入的精度一致：

复数输入：

高精度的高效计算：

自动逐项计算数组中每个元素的值：

或用 MatrixFunction 计算矩阵形式的 MittagLefflerE 函数：

用 Around 计算普通的统计区间：

特殊值 (5)

自动产生简化的精确值：

符号式计算：

对于和的较小整数值，MittagLefflerE 可以用初等函数表示：

其他情况下使用 FunctionExpand：

无穷处的值：

求当 MittagLefflerE[1/2,x]=0.5 时， x 的值：

可视化 (3)

为的整数值绘制 MittagLefflerE 函数图：

绘制非整数值的 MittagLefflerE 函数图：

绘制实部：

绘制虚部：

函数的属性 (8)

是针对所有和实数而定义的：

MittagLefflerE 的复定义域上也一样：

MittagLefflerE 有镜像属性：

MittagLefflerE 按元素线性作用于列表：

当，MittagLefflerE 是一个解析函数：

当，该函数有奇点和断点：

为单射函数：

不是满射：

为非负：

简化为：

微分 (3)

关于 z 的一阶导数：

关于 z 的高阶导数：

绘制 a=1/4 时关于 z 的高阶导数：

使用 FunctionExpand 求与参数相关的导数：

积分 (2)

MittagLefflerE 的不定积分：

更多积分：

级数展开 (2)

用 Series 求泰勒展开式：

绘制附近的前三个近似式：

普通点处的泰勒展开式：

分数阶微分方程 (3)

MittagLefflerE 在表达具有常数系数的分数 DE 解时起着重要作用：

验证解：

绘制解：

求解包含两个不同阶次的 Caputo 导数的常数分式 DE：

求解由两个向量形式的分数阶微分方程组成的方程组：

绘制解：

绘制解的参数图：

积分变换 (1)

特定 MittagLefflerE 函数的拉普拉斯变换：

在域的 ComplexPlot：

通过应用 InverseLaplaceTransform 变换回时域，并得到原始表达式：

应用 (5)

带分数指数的代数函数的 InverseLaplaceTransform 可以用 MittagLefflerE 表示：

定义 Mittag–Leffler 随机变量，其中：

Mittag–Leffler 随机变量与正稳定随机变量相关：

生成随机变量，并且将直方图与分布密度比较：

矩阵和向量：

定义一个函数，用于根据给定矩阵和向量计算 Krylov 矩阵：

计算矩阵的特征值：

具有常数系数的线性 Caputo 微分方程可以使用 MittagLefflerE 以及 Krylov 矩阵和 Vandermonde 矩阵的逆矩阵来求解：

验证 DSolveValue 是否能得到相同的结果：

Carlitz 将 -排列定义为连续运行个递增元素、跟着是个递增元素的排列. 下图说明了、的情况：

生成所有长度为 8 的排列：

对长度为 8 的 (3,2)- 排列的进行计数：

定义 Olivier 函数：

- 排列数量的生成函数可以用 Olivier 函数的比值来表示. 利用生成函数计算长度为 8 的 (3,2)- 排列数量：

通用开普勒方程可用于从初始时间出发，预测轨道天体在给定时间的位置和速度. 下面是火星从给定初始时间开始的日心位置和速度矢量：

计算位置和速度矢量的大小：

计算初始径向速度

根据活力方程（vis-viva equation）计算半长轴的倒数：

估算 8 小时后火星的位置和速度矢量：

定义在开普勒方程的通用变量公式中出现的 Stumpff 函数：

根据开普勒宇宙方程求解“宇宙异常”（universal anomaly）：

根据宇宙异常现象计算拉格朗日系数：

计算八小时后的位置矢量：

与真实值进行比较：

计算拉格朗日系数相对于时间的导数：

计算八小时后的速度矢量：

与真实值进行比较：

属性和关系 (4)

Mittag–Leffler 函数在微分下是闭合的：

对于较小非负整数，函数简化为基本函数：

的较大非负整数值给出了 HypergeometricPFQ 的结果：

对于非负半整数，简化为 HypergeometricPFQ 函数之和：

Mittag–Leffler 函数的定义和：

对于特定的，也许能够用 HypergeometricPFQ 函数来表示和：

与 MittagLefflerE 的输出相比较：

MittagLefflerE 函数族可以用 FoxH 表示：

顶部