MomentOfInertiaCopy to clipboard.
✖
MomentOfInertia
詳細とオプション

- 慣性モーメントは,回転の慣性,断面の慣性モーメント,質量慣性モーメントとしても知られている.慣性モーメント行列は回転慣性行列あるいは角質量行列としても知られている.
- 慣性モーメントは剛体の回転加速度に対しての抵抗であり,並進加速度に対する抵抗である質量の回転類似である.
-
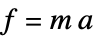
並進加速度 力 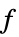 ,加速度
,加速度 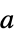 ,質量
,質量 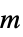
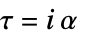
回転加速度 トルク 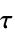 ,回転加速度
,回転加速度 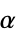 ,慣性モーメント
,慣性モーメント 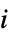
- MomentOfInertia[reg,pt]は,点 pt についての慣性モーメント行列を与え,以下で与えられる.
-
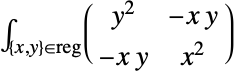
2D慣性モーメント行列 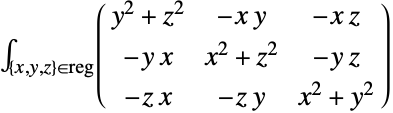
3D慣性モーメント行列 - ただし,reg は-pt 平行移動された領域 reg である.
- 慣性モーメント行列 ℐ を使い,式
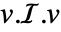 を通して任意の方向 v への慣性を計算することができる.2Dでは v は
を通して任意の方向 v への慣性を計算することができる.2Dでは v は 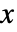 -
-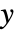 平面でなければならない. »
平面でなければならない. » - MomentOfInertiaは剛体の質量密度が一定であるという仮定の下に結果を計算する.
- 変化する質量密度
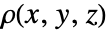 については,IntegrateあるいはNIntegrateを使い,以下の式に従って対応する慣性モーメント行列を計算する. »
については,IntegrateあるいはNIntegrateを使い,以下の式に従って対応する慣性モーメント行列を計算する. » -
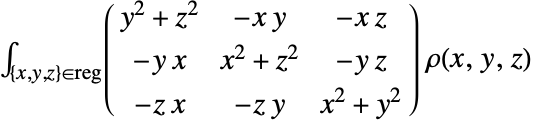
例題
すべて開くすべて閉じる例 (4)基本的な使用例
https://wolfram.com/xid/04z64adgdecc69xc-gif1l8
https://wolfram.com/xid/04z64adgdecc69xc-dxpuvw
ベクトルが省略された場合は,その点の周りの慣性モーメント行列が与えられる:
https://wolfram.com/xid/04z64adgdecc69xc-b7vsb5
この行列と正規化されたベクトルを使って,任意の軸の周りの慣性モーメントを求めることができる:
https://wolfram.com/xid/04z64adgdecc69xc-fhzh11
点が省略された場合は,質量の中心の周りの慣性モーメント行列が与えられる:
https://wolfram.com/xid/04z64adgdecc69xc-ha5tuu
これはRegionCentroidで中心点を指定することに等しい:
https://wolfram.com/xid/04z64adgdecc69xc-bod87p
https://wolfram.com/xid/04z64adgdecc69xc-4rtcl
スコープ (24)標準的な使用例のスコープの概要
特別な領域 (15)
長さ ![]() ,幅
,幅 ![]() のRectangle:
のRectangle:
https://wolfram.com/xid/04z64adgdecc69xc-nvigpk
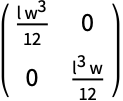
https://wolfram.com/xid/04z64adgdecc69xc-7wwgu2

半径 ![]() のDisk:
のDisk:
https://wolfram.com/xid/04z64adgdecc69xc-gx6l99
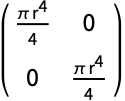
https://wolfram.com/xid/04z64adgdecc69xc-ioo0wr

https://wolfram.com/xid/04z64adgdecc69xc-bs8cju
https://wolfram.com/xid/04z64adgdecc69xc-mdhlxy

半径が ![]() と
と ![]() のAnnulus:
のAnnulus:
https://wolfram.com/xid/04z64adgdecc69xc-fe27qh
https://wolfram.com/xid/04z64adgdecc69xc-27z5zv

長さ ![]() ,半径
,半径 ![]() のStadiumShape:
のStadiumShape:
https://wolfram.com/xid/04z64adgdecc69xc-gkz0nz
https://wolfram.com/xid/04z64adgdecc69xc-7zxt82

辺の長さが ![]() と
と ![]() の直角Triangle:
の直角Triangle:
https://wolfram.com/xid/04z64adgdecc69xc-bf3qbz
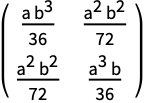
https://wolfram.com/xid/04z64adgdecc69xc-21gtt1

長さ ![]() ,幅
,幅 ![]() ,高さ
,高さ ![]() のCuboid:
のCuboid:
https://wolfram.com/xid/04z64adgdecc69xc-idvaps
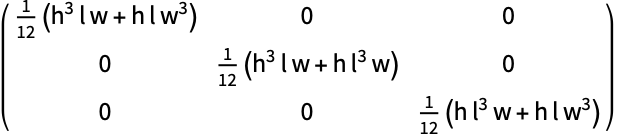
https://wolfram.com/xid/04z64adgdecc69xc-ckqdgo

半径 ![]() のBall:
のBall:
https://wolfram.com/xid/04z64adgdecc69xc-bu8dzr
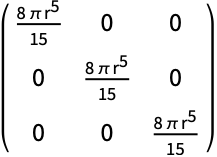
https://wolfram.com/xid/04z64adgdecc69xc-emum1c

半軸が ![]() ,
,![]() ,
,![]() のEllipsoid:
のEllipsoid:
https://wolfram.com/xid/04z64adgdecc69xc-hded6w
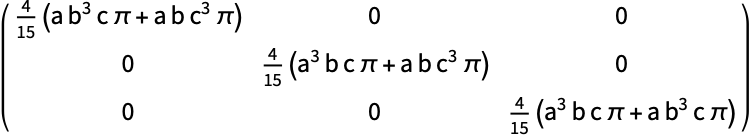
https://wolfram.com/xid/04z64adgdecc69xc-9aos3c

半径が ![]() と
と ![]() のSphericalShell:
のSphericalShell:
https://wolfram.com/xid/04z64adgdecc69xc-cdmeud
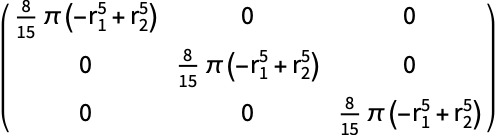
https://wolfram.com/xid/04z64adgdecc69xc-c6dgun
長さ ![]() ,半径
,半径 ![]() のCylinder:
のCylinder:
https://wolfram.com/xid/04z64adgdecc69xc-ca4q2o
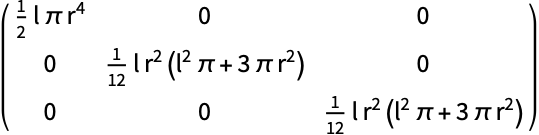
https://wolfram.com/xid/04z64adgdecc69xc-c32bqc

長さ ![]() ,半径
,半径 ![]() のCapsuleShape:
のCapsuleShape:
https://wolfram.com/xid/04z64adgdecc69xc-juyt2a
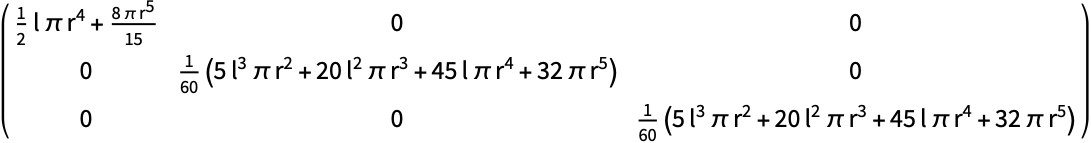
https://wolfram.com/xid/04z64adgdecc69xc-j9zyf7

辺の長さが ![]() ,
,![]() ,
,![]() の直角Tetrahedron:
の直角Tetrahedron:
https://wolfram.com/xid/04z64adgdecc69xc-f4lz5u
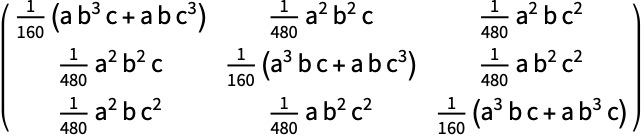
https://wolfram.com/xid/04z64adgdecc69xc-7xcsu6

辺の長さが ![]() と
と ![]() ,高さが
,高さが ![]() の直角Pyramid:
の直角Pyramid:
https://wolfram.com/xid/04z64adgdecc69xc-gml8k
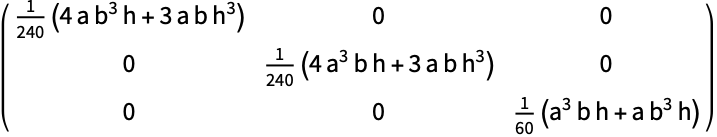
https://wolfram.com/xid/04z64adgdecc69xc-uto2ns

辺の長さが ![]() と
と ![]() ,高さが
,高さが ![]() の直角Prism:
の直角Prism:
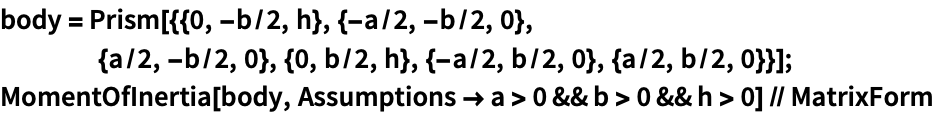
https://wolfram.com/xid/04z64adgdecc69xc-blx2bp
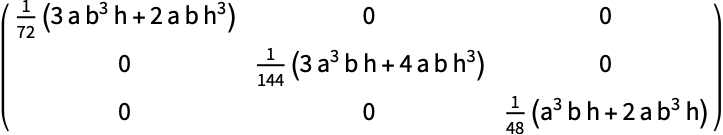
https://wolfram.com/xid/04z64adgdecc69xc-0tck87

数式定義領域 (2)
ImplicitRegionとして表現される円板の慣性行列:
https://wolfram.com/xid/04z64adgdecc69xc-len63u
https://wolfram.com/xid/04z64adgdecc69xc-kavh8q
ParametricRegionとして表現される円板の慣性モーメント:
https://wolfram.com/xid/04z64adgdecc69xc-8ufy
https://wolfram.com/xid/04z64adgdecc69xc-cl2ygx
https://wolfram.com/xid/04z64adgdecc69xc-bl8fm7
メッシュ領域 (2)
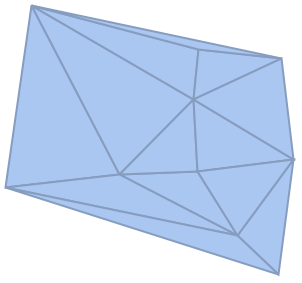
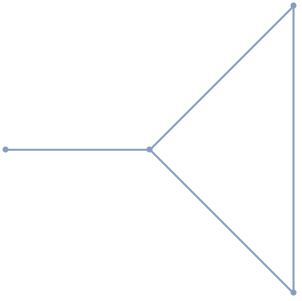
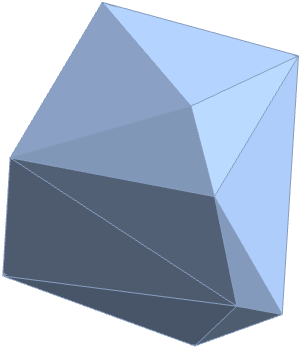
2DにおけるMeshRegionの慣性モーメント行列:
https://wolfram.com/xid/04z64adgdecc69xc-ib608p
https://wolfram.com/xid/04z64adgdecc69xc-esiyzj
https://wolfram.com/xid/04z64adgdecc69xc-mp72ll
https://wolfram.com/xid/04z64adgdecc69xc-cbepcr
https://wolfram.com/xid/04z64adgdecc69xc-dc3bst
https://wolfram.com/xid/04z64adgdecc69xc-ceqwoi
https://wolfram.com/xid/04z64adgdecc69xc-b8ss9k
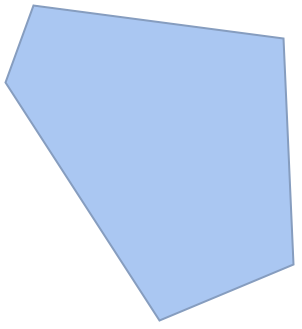
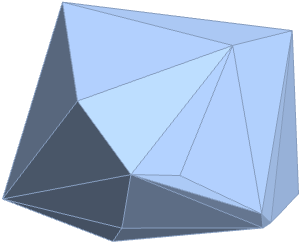
BoundaryMeshRegionの慣性モーメント行列:
https://wolfram.com/xid/04z64adgdecc69xc-ey15rx
https://wolfram.com/xid/04z64adgdecc69xc-b8mg48
https://wolfram.com/xid/04z64adgdecc69xc-dff1s9
https://wolfram.com/xid/04z64adgdecc69xc-o97lje
派生領域 (3)
RegionIntersectionの慣性モーメント:
https://wolfram.com/xid/04z64adgdecc69xc-d92fo3
https://wolfram.com/xid/04z64adgdecc69xc-doodgd

https://wolfram.com/xid/04z64adgdecc69xc-nk2dal
TransformedRegionの慣性モーメント行列:
https://wolfram.com/xid/04z64adgdecc69xc-b6muk5
https://wolfram.com/xid/04z64adgdecc69xc-8ezppp

https://wolfram.com/xid/04z64adgdecc69xc-cu2k8w
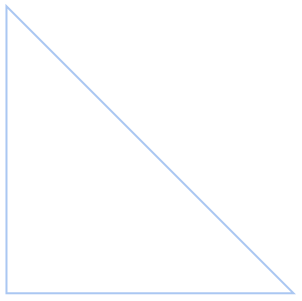
RegionBoundaryの慣性モーメント行列:
https://wolfram.com/xid/04z64adgdecc69xc-bklovj
https://wolfram.com/xid/04z64adgdecc69xc-dr7gcv
https://wolfram.com/xid/04z64adgdecc69xc-ca4mg4
地理的領域 (2)
MomentOfInertiaは地理実体の多角形に使うことができる:
https://wolfram.com/xid/04z64adgdecc69xc-3fl8vb
https://wolfram.com/xid/04z64adgdecc69xc-6dyfmr
GeoPositionを使った多角形:

https://wolfram.com/xid/04z64adgdecc69xc-1lk1dy
https://wolfram.com/xid/04z64adgdecc69xc-8vjhh8
GeoPositionXYZを使った多角形:

https://wolfram.com/xid/04z64adgdecc69xc-4dy58p
https://wolfram.com/xid/04z64adgdecc69xc-pzmsx0
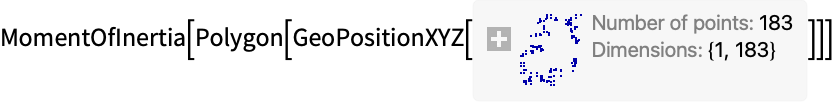
GeoPositionENUを使った多角形:

https://wolfram.com/xid/04z64adgdecc69xc-sz3fv8
https://wolfram.com/xid/04z64adgdecc69xc-pjpdg1

GeoGridPositionを使った多角形の慣性モーメント:

https://wolfram.com/xid/04z64adgdecc69xc-ipsiqu
https://wolfram.com/xid/04z64adgdecc69xc-yjciq7
アプリケーション (11)この関数で解くことのできる問題の例
MomentOfInertiaは質量密度が一定して1である物体の慣性モーメントを与える.長さ ![]() ,幅
,幅 ![]() ,高さ
,高さ ![]() で質量密度が一定して
で質量密度が一定して ![]() であるCuboidの慣性モーメントを計算する:
であるCuboidの慣性モーメントを計算する:
https://wolfram.com/xid/04z64adgdecc69xc-hckkew
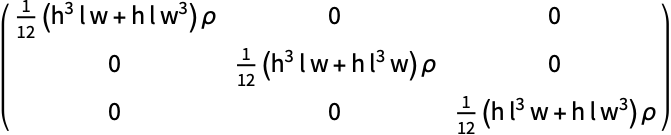
質量密度が ![]() の物体の質量はm=ρ Volume[body]で与えられる.慣性モーメントを物体の質量
の物体の質量はm=ρ Volume[body]で与えられる.慣性モーメントを物体の質量 ![]() を使って表す:
を使って表す:
https://wolfram.com/xid/04z64adgdecc69xc-i6ltbh
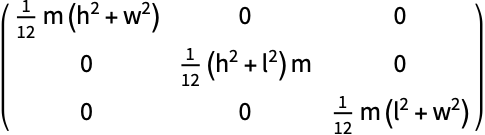

https://wolfram.com/xid/04z64adgdecc69xc-xzgy
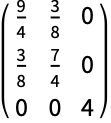
上部左の2×2部分行列は2D領域の慣性モーメントと同値である:
https://wolfram.com/xid/04z64adgdecc69xc-namxps
行列のその他の唯一の非零項目は対角上にある.これは![]() 軸周りの部分の極モーメントであり,垂直軸定理によって対角上の他の2項目の合計に等しい:
軸周りの部分の極モーメントであり,垂直軸定理によって対角上の他の2項目の合計に等しい:
https://wolfram.com/xid/04z64adgdecc69xc-dyh2p1
https://wolfram.com/xid/04z64adgdecc69xc-ffbxd1
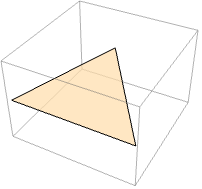
物体の主軸は慣性モーメント行列の固有ベクトルによって与えられる:
https://wolfram.com/xid/04z64adgdecc69xc-edgrn
https://wolfram.com/xid/04z64adgdecc69xc-f9lbyb
https://wolfram.com/xid/04z64adgdecc69xc-g9gcba
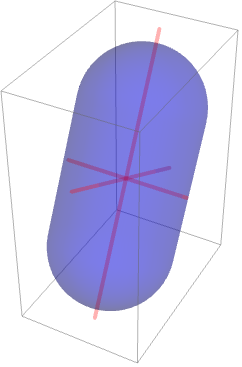
慣性モーメント行列が対角行列の場合,主軸は座標軸に一致する:
https://wolfram.com/xid/04z64adgdecc69xc-d5esyk
https://wolfram.com/xid/04z64adgdecc69xc-hwm7xu
https://wolfram.com/xid/04z64adgdecc69xc-chhoxw
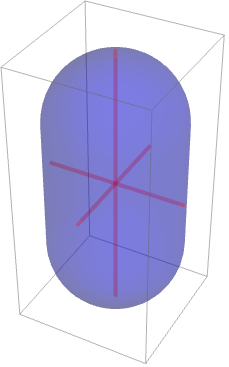
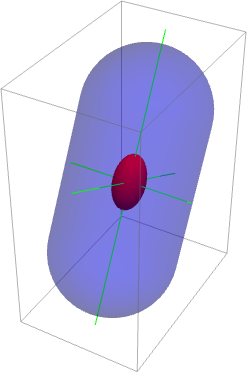
慣性モーメント行列はEllipsoidを定義する行列であると考えることができる:
https://wolfram.com/xid/04z64adgdecc69xc-f26v0o
慣性楕円体は![]() として定義することができる.ただし,
として定義することができる.ただし,![]() は重心である:
は重心である:
https://wolfram.com/xid/04z64adgdecc69xc-bn7pm9
Eigensystemを使って主軸を求める:
https://wolfram.com/xid/04z64adgdecc69xc-mx8dp
https://wolfram.com/xid/04z64adgdecc69xc-gmbd16
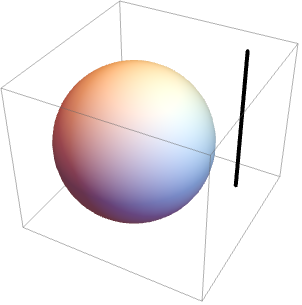
回転剛体の角運動量は ![]() で与えられる.ただし,
で与えられる.ただし,![]() は慣性モーメントであり,
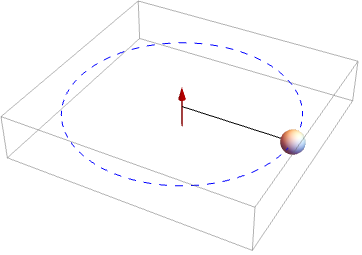
は慣性モーメントであり,![]() は角速度である.半径が1で一様密度が1の球体が
は角速度である.半径が1で一様密度が1の球体が ![]() 軸の周囲を長さが調節可能な
軸の周囲を長さが調節可能な ![]() である紐の上で回転すると仮定する.
である紐の上で回転すると仮定する.![]() のとき,角速度は
のとき,角速度は ![]() である.角速度
である.角速度 ![]() を
を ![]() の関数として求める:
の関数として求める:

https://wolfram.com/xid/04z64adgdecc69xc-blvg0
https://wolfram.com/xid/04z64adgdecc69xc-dp9fv3
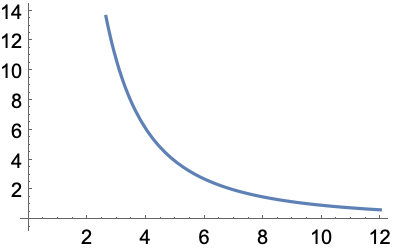
物体にトルクが適用されなければその角運動量 ![]() は一定のままであるという角運動量保存則に従って
は一定のままであるという角運動量保存則に従って ![]() を計算する:
を計算する:
https://wolfram.com/xid/04z64adgdecc69xc-bxpz3o
https://wolfram.com/xid/04z64adgdecc69xc-bzjo1f
回転剛体の運動エネルギーは ![]() で与えられる.ただし,
で与えられる.ただし,![]() は慣性モーメントで
は慣性モーメントで ![]() は角速度である.半径
は角速度である.半径 ![]() で一様密度
で一様密度 ![]() の球体が角速度
の球体が角速度 ![]() で中心を通る軸の周りを回転する際の運動エネルギーを計算する:
で中心を通る軸の周りを回転する際の運動エネルギーを計算する:
https://wolfram.com/xid/04z64adgdecc69xc-djo5wc
https://wolfram.com/xid/04z64adgdecc69xc-chn0uk
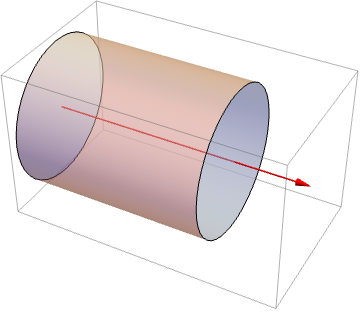
運動エネルギー回生システム(KERS)は,ブレーキをかけたときの車の運動エネルギーを保存する.エネルギーは半径 ![]() ,長さ
,長さ ![]() の回転スチールシリンダーに保存されると仮定する.スチールの密度が
の回転スチールシリンダーに保存されると仮定する.スチールの密度が![]() であると仮定すると,
であると仮定すると,![]() のエネルギーを保存するためには,このシリンダーはどの程度の速度で回転しなければならないだろうか:
のエネルギーを保存するためには,このシリンダーはどの程度の速度で回転しなければならないだろうか:
https://wolfram.com/xid/04z64adgdecc69xc-bqgsw1
https://wolfram.com/xid/04z64adgdecc69xc-fdpiki
https://wolfram.com/xid/04z64adgdecc69xc-zcihi
https://wolfram.com/xid/04z64adgdecc69xc-cn1tdv
https://wolfram.com/xid/04z64adgdecc69xc-g2ajis
剛体の運動エネルギーは ![]() で与えられる.ただし,
で与えられる.ただし,![]() は角速度で
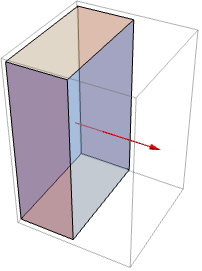
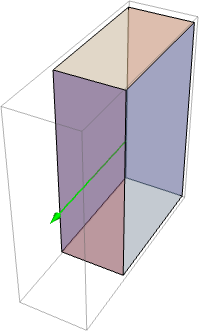
は角速度で ![]() は慣性モーメント行列である.辺の長さが 2,4,6 の直方体が異なる軸の周りを回転する際の回転エネルギーを求める.どの場合も,回転物体の質量は等しいが,回転軸と相対的にどのように質量が分配されるかは異なり,慣性モーメントで表される:
は慣性モーメント行列である.辺の長さが 2,4,6 の直方体が異なる軸の周りを回転する際の回転エネルギーを求める.どの場合も,回転物体の質量は等しいが,回転軸と相対的にどのように質量が分配されるかは異なり,慣性モーメントで表される:
https://wolfram.com/xid/04z64adgdecc69xc-blyj36
https://wolfram.com/xid/04z64adgdecc69xc-k41yb
https://wolfram.com/xid/04z64adgdecc69xc-c50spm
https://wolfram.com/xid/04z64adgdecc69xc-h2q081
https://wolfram.com/xid/04z64adgdecc69xc-l632o7
https://wolfram.com/xid/04z64adgdecc69xc-ipq6jp
https://wolfram.com/xid/04z64adgdecc69xc-dh0v
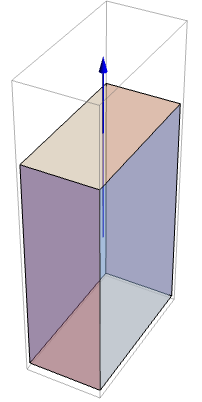
回転剛体について,トルク ![]() と角加速度
と角加速度 ![]() の関係は
の関係は ![]() で与えられる.ただし,
で与えられる.ただし,![]() は慣性モーメントである.一辺の長さが1メートルで角加速度が
は慣性モーメントである.一辺の長さが1メートルで角加速度が![]() の鉛の立方体に必要なトルクを計算する:
の鉛の立方体に必要なトルクを計算する:
https://wolfram.com/xid/04z64adgdecc69xc-b926cp
https://wolfram.com/xid/04z64adgdecc69xc-mtex
https://wolfram.com/xid/04z64adgdecc69xc-d5nmx7
https://wolfram.com/xid/04z64adgdecc69xc-o3rvo
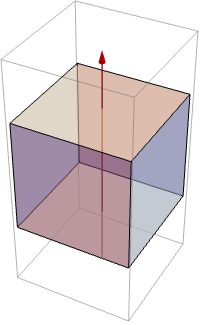
平行軸の定理は,任意の軸の周りの慣性モーメント ![]() と物体の中心を通る平行軸の周りの慣性モーメント
と物体の中心を通る平行軸の周りの慣性モーメント ![]() の関係
の関係 ![]() を与える.ただし,
を与える.ただし,![]() は総質量で
は総質量で ![]() は軸の間の距離である:
は軸の間の距離である:

https://wolfram.com/xid/04z64adgdecc69xc-lqnq4i
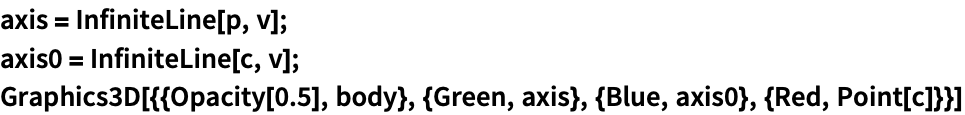
https://wolfram.com/xid/04z64adgdecc69xc-d8kowu
https://wolfram.com/xid/04z64adgdecc69xc-dmlekm
特性と関係 (11)この関数の特性および他の関数との関係
点が省略された場合は,RegionCentroidがデフォルトであると解釈される:
https://wolfram.com/xid/04z64adgdecc69xc-bj6nk3
https://wolfram.com/xid/04z64adgdecc69xc-bud3d2
指定された点 ![]() について,物体を
について,物体を![]() だけ平行移動して原点の周りの慣性モーメントを計算しても同じ結果が得られる:
だけ平行移動して原点の周りの慣性モーメントを計算しても同じ結果が得られる:
https://wolfram.com/xid/04z64adgdecc69xc-cuzntj
https://wolfram.com/xid/04z64adgdecc69xc-ms81m
https://wolfram.com/xid/04z64adgdecc69xc-7n316
https://wolfram.com/xid/04z64adgdecc69xc-bbi6y1
https://wolfram.com/xid/04z64adgdecc69xc-bx62w3
https://wolfram.com/xid/04z64adgdecc69xc-kr9vf1
Integrateを使って質量密度 ![]() が変化する物体についての慣性モーメントを計算する:
が変化する物体についての慣性モーメントを計算する:
https://wolfram.com/xid/04z64adgdecc69xc-phb11
https://wolfram.com/xid/04z64adgdecc69xc-c1r3sj
https://wolfram.com/xid/04z64adgdecc69xc-ctl2yt
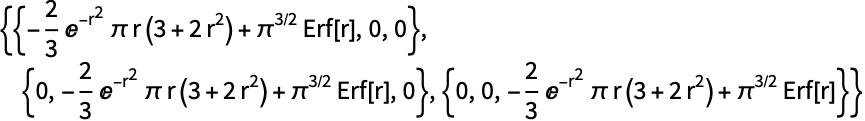
https://wolfram.com/xid/04z64adgdecc69xc-gp8bo8
https://wolfram.com/xid/04z64adgdecc69xc-futecu
https://wolfram.com/xid/04z64adgdecc69xc-eutki0
https://wolfram.com/xid/04z64adgdecc69xc-xlzjk
2Dの慣性モーメント行列はRegionMomentを使って計算することができる:

https://wolfram.com/xid/04z64adgdecc69xc-graeo1
https://wolfram.com/xid/04z64adgdecc69xc-c4bbb8
https://wolfram.com/xid/04z64adgdecc69xc-e2bgrg
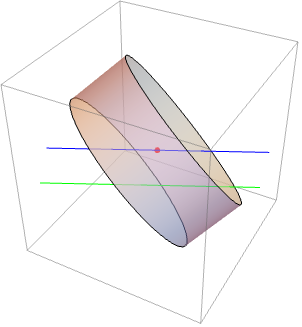
3Dの慣性モーメント行列はRegionMomentを使って計算することができる:

https://wolfram.com/xid/04z64adgdecc69xc-bcke3x
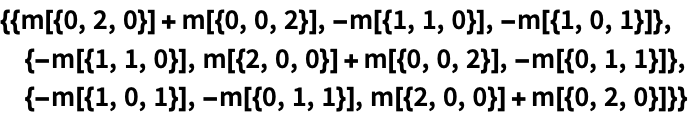
https://wolfram.com/xid/04z64adgdecc69xc-hfbrk5
https://wolfram.com/xid/04z64adgdecc69xc-gf5yyo
Pointの慣性モーメントは点から軸までの距離の二乗である:

https://wolfram.com/xid/04z64adgdecc69xc-io9oah
https://wolfram.com/xid/04z64adgdecc69xc-letpk
https://wolfram.com/xid/04z64adgdecc69xc-lp7dgb
https://wolfram.com/xid/04z64adgdecc69xc-fz3scm
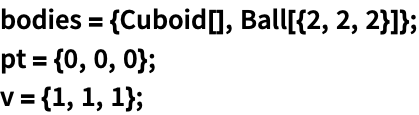
https://wolfram.com/xid/04z64adgdecc69xc-jhrd0q
https://wolfram.com/xid/04z64adgdecc69xc-u8u8j
https://wolfram.com/xid/04z64adgdecc69xc-migg17
Wolfram Research (2016), MomentOfInertia, Wolfram言語関数, https://reference.wolfram.com/language/ref/MomentOfInertia.html.テキスト
Wolfram Research (2016), MomentOfInertia, Wolfram言語関数, https://reference.wolfram.com/language/ref/MomentOfInertia.html.
Wolfram Research (2016), MomentOfInertia, Wolfram言語関数, https://reference.wolfram.com/language/ref/MomentOfInertia.html.CMS
Wolfram Language. 2016. "MomentOfInertia." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/MomentOfInertia.html.
Wolfram Language. 2016. "MomentOfInertia." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/MomentOfInertia.html.APA
Wolfram Language. (2016). MomentOfInertia. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/MomentOfInertia.html
Wolfram Language. (2016). MomentOfInertia. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/MomentOfInertia.htmlBibTeX
@misc{reference.wolfram_2025_momentofinertia, author="Wolfram Research", title="{MomentOfInertia}", year="2016", howpublished="\url{https://reference.wolfram.com/language/ref/MomentOfInertia.html}", note=[Accessed: 13-April-2025
]}BibLaTeX
@online{reference.wolfram_2025_momentofinertia, organization={Wolfram Research}, title={MomentOfInertia}, year={2016}, url={https://reference.wolfram.com/language/ref/MomentOfInertia.html}, note=[Accessed: 13-April-2025
]}