MomentOfInertia[reg,pt,v]
计算围绕过 pt 点沿 v 方向的轴转动的区域 reg 的转动惯量.
MomentOfInertia[reg]
计算区域 reg 对质心的转动惯量矩阵.
MomentOfInertia[reg,pt]
计算相对点 pt 的转动惯量矩阵.


MomentOfInertia
MomentOfInertia[reg,pt,v]
计算围绕过 pt 点沿 v 方向的轴转动的区域 reg 的转动惯量.
MomentOfInertia[reg]
计算区域 reg 对质心的转动惯量矩阵.
MomentOfInertia[reg,pt]
计算相对点 pt 的转动惯量矩阵.
更多信息和选项

- 转动惯量惯又叫做质量惯性矩或惯量矩. 转动惯量惯矩阵又叫做质量惯性矩矩阵或惯量矩矩阵.
- 转动惯量是刚体对转动加速度的抵抗. 它在转动运动中的作用类似于平动中的质量. 质量是对平动加速度的抵抗.
-
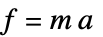
平动加速度 力 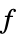 , 加速度
, 加速度  , 质量
, 质量 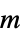

转动加速度 力矩 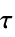 , 转动加速度
, 转动加速度 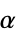 , 转动惯量
, 转动惯量 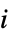
- MomentOfInertia[reg,pt] 给出关于点 pt 的转动惯量,并由下式得到:
-
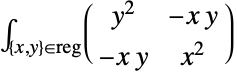
二维转动惯量矩阵 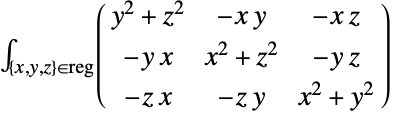
三维转动惯量矩阵 - 其中 reg 由区域 reg 平移 -pt 得到.
- 转动惯量矩阵 ℐ 通过公式
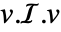 可用来计算沿任何方向 v 的转动惯量. 在二维情况下,v 必须在
可用来计算沿任何方向 v 的转动惯量. 在二维情况下,v 必须在 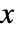 -
-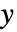 平面内. »
平面内. » - MomentOfInertia 是假定区域的质量密度为常数的情况下给出计算结果.
- 对于变质量密度
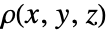 , 要按照以下公式用 Integrate 或 NIntegrate 计算出转动惯量矩阵. »
, 要按照以下公式用 Integrate 或 NIntegrate 计算出转动惯量矩阵. » -
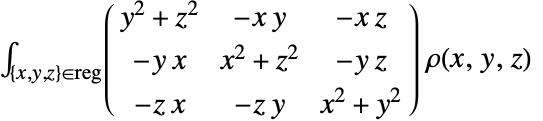
范例
打开所有单元 关闭所有单元基本范例 (4)
运用这个矩阵和一个归一化的向量,可以求出围绕任何轴的转动惯量:
这相当于通过 RegionCentroid 来指定中心点:
范围 (24)
特殊区域 (15)
长 ![]() ,宽
,宽 ![]() 的 Rectangle:
的 Rectangle:
半径为 ![]() 的 Disk:
的 Disk:
半径为 ![]() 和
和 ![]() 的 Annulus:
的 Annulus:
长为 ![]() ,半径为
,半径为 ![]() 的 StadiumShape:
的 StadiumShape:
边长为 ![]() 和
和 ![]() 的正 Triangle:
的正 Triangle:
长为 ![]() ,宽为
,宽为 ![]() ,高为
,高为 ![]() 的 Cuboid:
的 Cuboid:
半径为 ![]() 的 Ball:
的 Ball:
半轴为 ![]() ,
,![]() 和
和 ![]() 的 Ellipsoid:
的 Ellipsoid:
半径为 ![]() 和
和 ![]() 的 SphericalShell:
的 SphericalShell:
长为 ![]() ,半径为
,半径为 ![]() 的 Cylinder:
的 Cylinder:
长为 ![]() ,半径为
,半径为 ![]() 的 CapsuleShape:
的 CapsuleShape:
边长为 ![]() ,
,![]() 和
和 ![]() 的长方形 Tetrahedron:
的长方形 Tetrahedron:
边长为 ![]() 和
和 ![]() ,高为
,高为 ![]() 的长方形 Pyramid:
的长方形 Pyramid:
边长为 ![]() 和
和 ![]() ,高为
,高为 ![]() 的长方形 Prism:
的长方形 Prism:
公式确定的区域 (2)
网格区域 (2)
导出区域 (3)
地理区域 (2)
MomentOfInertia 适用于地理实体的边界多边形:
Polygon 与 GeoPosition 一起使用:
Polygon 与 GeoPositionXYZ 一起使用:
Polygon 与 GeoPositionENU 一起使用:
Polygon 与 GeoGridPosition 一起使用所得边界多边形的惯性矩:
应用 (11)
MomentOfInertia 给出的是质量密度为 1 的物体的转动惯量. 计算长 ![]() ,宽
,宽 ![]() ,高
,高 ![]() ,且质量密度为
,且质量密度为 ![]() 的 Cuboid 的转动惯量:
的 Cuboid 的转动惯量:
一个具有常数质量密度 ![]() 的物体的质量由 m=ρ Volume[body] 给出. 将物体的转动惯量用质量
的物体的质量由 m=ρ Volume[body] 给出. 将物体的转动惯量用质量 ![]() 的形式表示:
的形式表示:
其余仅有的矩阵元只处于对角线上. 它是关于 ![]() 轴的极惯性矩,根据垂直轴定理,它应等于其他两个对角矩阵元之和:
轴的极惯性矩,根据垂直轴定理,它应等于其他两个对角矩阵元之和:
转动惯量矩阵可以看成一个用来定义 Ellipsoid 的矩阵:
用 Eigensystem 求主轴:
一个转动刚体的角动量为 ![]() ,其中
,其中 ![]() 为转动惯量,
为转动惯量,![]() 为角速度. 假设一个半径为 1,均匀质量密度为 1 的球系在长为
为角速度. 假设一个半径为 1,均匀质量密度为 1 的球系在长为 ![]() 的弦上绕
的弦上绕 ![]() 轴转动. 弦长可调节. 当
轴转动. 弦长可调节. 当 ![]() 时,角速度为
时,角速度为 ![]() . 求角速度
. 求角速度 ![]() 与
与 ![]() 的函数关系:
的函数关系:
由角动量守恒定律得知,如果一个物体没有受到外力矩的作用,则其角动量 ![]() 保持不变. 根据这一定理来计算
保持不变. 根据这一定理来计算 ![]() :
:
转动刚体的动能为 ![]() ,其中
,其中 ![]() 为转动惯量,
为转动惯量,![]() 为角速度. 一个半径为
为角速度. 一个半径为 ![]() ,均匀密度为
,均匀密度为 ![]() 的球围绕通过其中心的轴以角速度
的球围绕通过其中心的轴以角速度 ![]() 转动. 求球的动能:
转动. 求球的动能:
动能回收系统(KERS)在汽车刹车时储存其动能. 假定能量是储存在一个半径为 ![]() ,长
,长 ![]() 的转动的钢制圆柱体上. 圆柱体要转多快才能储存
的转动的钢制圆柱体上. 圆柱体要转多快才能储存 ![]() 的能量,假定钢的密度为
的能量,假定钢的密度为 ![]() :
:
刚体的动能由 ![]() 给出,其中
给出,其中 ![]() 为一个角速度向量,
为一个角速度向量, ![]() 为转动惯量矩阵. 求一个边长为 2, 4 和 6 的长方体围绕不同的轴的转动能量. 对所有情况,旋转体的质量都是相同的,但对于不同转动轴,质量的分布却是不同的,它是用转动惯量来表示的:
为转动惯量矩阵. 求一个边长为 2, 4 和 6 的长方体围绕不同的轴的转动能量. 对所有情况,旋转体的质量都是相同的,但对于不同转动轴,质量的分布却是不同的,它是用转动惯量来表示的:
一个转动刚体所受力矩 ![]() 和角加速度
和角加速度 ![]() 的关系是
的关系是 ![]() ,其中
,其中 ![]() 为转动惯量. 计算一个边长为一米的铅制正方体在角加速度为
为转动惯量. 计算一个边长为一米的铅制正方体在角加速度为 ![]() 时所需要的力矩:
时所需要的力矩:
平行轴定理给出了围绕某一个轴的转动惯量 ![]() 和围绕一个通过质心且与其平行的轴的转动惯量
和围绕一个通过质心且与其平行的轴的转动惯量 ![]() 之间的一个关系
之间的一个关系 ![]() ,其中
,其中 ![]() 为总质量,
为总质量,![]() 为两轴之间的距离:
为两轴之间的距离:
属性和关系 (11)
如果省略了转动点,则以 RegionCentroid 为默认值:
对于一个给定的点 ![]() ,将物体平移
,将物体平移 ![]() 后再计算其相对原点的转动惯量将得到相同的结果:
后再计算其相对原点的转动惯量将得到相同的结果:
用 Integrate 来计算一个具有变质量密度 ![]() 的物体的转动惯量:
的物体的转动惯量:
二维时的转动惯量矩阵可以用 RegionMoment 来计算:
三维时的转动惯量矩阵可以用 RegionMoment 来计算:
一个点 Point 的转动惯量为这个点到轴的距离的平方:
文本
Wolfram Research (2016),MomentOfInertia,Wolfram 语言函数,https://reference.wolfram.com/language/ref/MomentOfInertia.html.
CMS
Wolfram 语言. 2016. "MomentOfInertia." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/MomentOfInertia.html.
APA
Wolfram 语言. (2016). MomentOfInertia. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/MomentOfInertia.html 年
BibTeX
@misc{reference.wolfram_2025_momentofinertia, author="Wolfram Research", title="{MomentOfInertia}", year="2016", howpublished="\url{https://reference.wolfram.com/language/ref/MomentOfInertia.html}", note=[Accessed: 16-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_momentofinertia, organization={Wolfram Research}, title={MomentOfInertia}, year={2016}, url={https://reference.wolfram.com/language/ref/MomentOfInertia.html}, note=[Accessed: 16-February-2026]}