NonlinearModelFit
NonlinearModelFit[{{x1,y1},{x2,y2},…},form,{β1,…},x]
自由母数 βiを使って各 xiに yiをフィットする式 form で非線形モデルを構築する.
NonlinearModelFit[data,form,params,{x1,…}]
form が変数 xkに依存する非線形モデルを構築する.
NonlinearModelFit[data,{form,cons},params,{x1,…}]
母数の制約条件 cons に従う非線形モデルを構築する.
詳細とオプション



- NonlinearModelFitは,自由母数を持つ一般的な数式で入力データをモデル化しようとする.
- NonlinearModelFitは,もとの
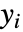 が,平均
が,平均 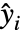 および共通標準偏差で独立の正規分布に従うという仮定のもとに,
および共通標準偏差で独立の正規分布に従うという仮定のもとに,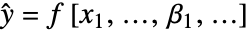 の形の非線形モデルを作成する.
の形の非線形モデルを作成する. - NonlinearModelFitは,自身が構築した非線形モデルを表す記号的なFittedModelオブジェクトを返す.モデルの特性と診断は model["property"]で得ることができる.
- 特定の点 x1, …におけるNonlinearModelFitからの最もよくフィットした関数の値は model[x1,…]で得ることができる.
- NonlinearModelFit[data,form,pars,vars]の最もよくフィットした関数はFindFit[data,form,pars,vars]の結果に等しい.
- NonlinearModelFit[data,form,{{β1,val1},…},vars]は,{β1->val1,…}とのフィットについての検索を始める.
- 次は,data の可能な形である.
-
{y1,y2,…} {{1,y1},{2,y2},…}という形式に等しい {{x11,x12,…,y1},…} 独立した値 xijと応答 yiのリスト {{x11,x12,…}y1,…} 入力値と応答の間の規則のリスト {{x11,x12,…},…}{y1,y2,…} 入力値と応答のリストの間の規則 {{x11,…,y1,…},…}n 行列の第 n 列をフィットする 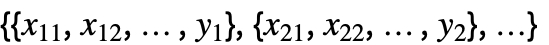 のような多変量のデータの場合,座標 xi1, xi2, …の数は変数 xiの数と一致しなければならない.
のような多変量のデータの場合,座標 xi1, xi2, …の数は変数 xiの数と一致しなければならない.- データ点は近似実数でよい.不確かさはAroundを使って指定できる.
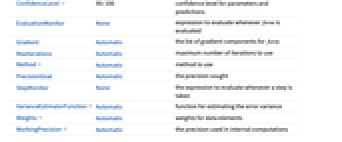
- NonlinearModelFitで使用可能なオプション
-
AccuracyGoal Automatic 目標確度の桁数 ConfidenceLevel 95/100 母数と予測の信頼水準 EvaluationMonitor None form が評価されるたびに評価される式 Gradient Automatic form についての購勾配要素のリスト MaxIterations Automatic 使用する最大反復回数 Method Automatic 使用するメソッド PrecisionGoal Automatic 目標精度 StepMonitor None ステップが取られるたびに評価される式 VarianceEstimatorFunction Automatic 誤差分散を推定する関数 Weights Automatic データ要素の重み WorkingPrecision Automatic 内部計算で使われる精度 - ConfidenceLevel->p のとき,確率 p の信頼区間は母数と予測区間について計算される.
- Weights->{w1,w2,…}の設定では,yiの誤差分散は
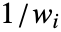 に比例すると推定される.
に比例すると推定される. - Weights->Automaticの設定では,データが厳密値を含んでいるなら重みは1に設定される.データがAroundの値を含んでいるなら,重みは
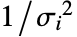 に設定される,ただし,
に設定される,ただし,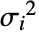 は応答分散の合計である.
は応答分散の合計である. - 応答分散の合計
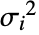 は,初期応答分散 Δyi2と独立値分散
は,初期応答分散 Δyi2と独立値分散 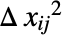 の関数である.
の関数である. - 不確かさ
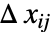 は,AroundReplaceを使ってモデル全体に伝播され,結果の分散が応答分散 Δyi2に加えられる.関数 FindRootを内部的に使ってFasanoおよびVioのメソッドによる自己一貫性のある解が求められる.
は,AroundReplaceを使ってモデル全体に伝播され,結果の分散が応答分散 Δyi2に加えられる.関数 FindRootを内部的に使ってFasanoおよびVioのメソッドによる自己一貫性のある解が求められる. - VarianceEstimatorFunction->f の設定では,一般分散は f[res,w]で推定される.ただし,res={y1-
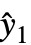 ,y2-
,y2-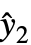 ,…}は残差のリスト,w は重みのリストである.
,…}は残差のリスト,w は重みのリストである. - VarianceEstimatorFunction->(1&)およびWeights->{1/Δy12,1/Δy22,…}を使うと,Δyiは測定 yiの既知の不確実性として扱われ,母数標準誤差は事実上重みのみから計算される.
- 次は,使用可能なMethodの設定である.
-
"ConjugateGradient" 非線形共役勾配 "Gradient" 傾斜降下 "LevenbergMarquardt" 最小二乗のガウス・ニュートン法 "Newton" ニュートン法 "QuasiNewton" 擬似ニュートンBFGS "InteriorPoint" 内点法 "NMinimize" 最適化にNMinimizeを使う Automatic 自動デフォルトメソッド - 上記以外のメソッドの選択肢はMethod->{…,opts}で得ることができる.
- The Methodオプションは,チュートリアル「制約条件のない最適化:局所的最小化の方法」で指定されているように,局所最適化法を取ることができる. »
- "NMinimize"法の下位メソッドとして任意の大域的最適化法が指定できる.メソッドについてはチュートリアル「大域的非線形数値最適化」を参照されたい. »
- 制約条件付きのモデルの場合,近似的な正規性の仮定に基づいた特性値は有効ではなくなることがある.そのような値が計算された場合,生成された値は警告メッセージを伴う.
- model["property"]を使ったデータとフィットされた関数に関連する特性
-
"BestFit" フィットされた関数 "BestFitParameters" 母数の推定 "Data" 入力データあるいは計画行列と応答ベクトル "Function" 最もよくフィットした純関数 "Response" 入力データの応答値 "Weights" データをフィットするために使われる重み - 残差のタイプ
-
"FitResiduals" 実際の応答と予想された応答の差 "StandardizedResiduals" 各残差について標準誤差で割ったフィットの残差 "StudentizedResiduals" 単一の削除誤差推定で割ったフィットの残差 - 平方誤差の総和に関連した特性
-
"ANOVA" 分散データの分析 "EstimatedVariance" 誤差分散の推定 - 母数推定の特性と診断
-
"CorrelationMatrix" 漸近的な母数相関行列 "CovarianceMatrix" 漸近的な母数共分散行列 "ParameterEstimates" フィットされたパラメータ情報の表 "ParameterBias" 母数推定で推定される偏り "ParameterConfidenceRegion" 楕円体母数信頼領域 - 曲率診断特性
-
"CurvatureConfidenceRegion" 曲率診断の信頼区間 "FitCurvature" フィットされた曲率情報の表 "MaxIntrinsicCurvature" 最大内部曲率尺度 "MaxParameterEffectsCurvature" 最大母数効果曲率の尺度 - 影響力の統計量関連特性
-
"HatDiagonal" ハット行列の対角要素 "SingleDeletionVariances" 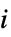
 番目のデータ点を除いた分散推定のリスト
番目のデータ点を除いた分散推定のリスト - 予測値関連特性
-
"MeanPredictionBands" 平均予測の信頼帯 "MeanPredictions" 平均予測の信頼区間 "PredictedResponse" データのフィットされた値 "SinglePredictionBands" 1回の観察に基づいた信頼帯 "SinglePredictions" 1界の観測の予測される応答についての信頼区間 - 適合度を測定する特性
-
"AdjustedRSquared" モデル母数の数に適応された 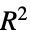
"AIC" 赤池情報量基準 "AICc" 有限サンプル修正AIC "BIC" ベイズ(Bayes)情報量基準 "RSquared" 決定係数 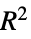
オプション
特性
例題
すべて開くすべて閉じるスコープ (15)
データ (7)
特性 (8)
影響力の統計量 (1)
一般化と拡張 (2)
ParametricNDSolveValueを使って微分方程式の解をキャッシュすることで計算をずっと速くする:
オプション (10)
ConfidenceLevel (1)
Method (3)
最小二乗目的関数を最小化するためにデフォルトメソッドを使う:
NMinimizeからの大域的最適化法を使ってより徹底した検索を行う:
Weights (4)
Aroundの値を使ってデータ点に異なる重みを与える:
Aroundの値を独立変数と応答の両方に使用する:
場合によっては,独立変数の不確かさを処理する求根アルゴリズムが標準的なオプション設定では収束しないかもしれない:
DampingFactorを下げ,MaxIterationsを上げてFixedPointアルゴリズムを使うと収束する:
WorkingPrecision (1)
アプリケーション (1)
特性と関係 (5)
NonlinearModelFitは正規分布に従う誤差を想定して線形および非線形のモデルをフィットする:
LinearModelFitは正規分布に従う誤差を想定して線形モデルをフィットする:
FindFitとNonlinearModelFitは等しいモデルをフィットする:
NonlinearModelFitを使ってフィットに関する追加的な情報を抽出することができる:
NonlinearModelFitは正規分布に従う応答を想定する:
LogitModelFitは二項分布に従う応答を想定する:
ProbitModelFitについても同じことが言える:
NonlinearModelFitはTimeSeriesのタイムスタンプを変数として使う:
NonlinearModelFitは,複数の経路のあるTemporalDataについては,経路ごとに作用する:
考えられる問題 (3)
NonlinearModelFitにおける決定係数 ![]() は,訂正されていないデータによって計算される:
は,訂正されていないデータによって計算される:
テキスト
Wolfram Research (2008), NonlinearModelFit, Wolfram言語関数, https://reference.wolfram.com/language/ref/NonlinearModelFit.html.
CMS
Wolfram Language. 2008. "NonlinearModelFit." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/NonlinearModelFit.html.
APA
Wolfram Language. (2008). NonlinearModelFit. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/NonlinearModelFit.html