NonlinearModelFit

NonlinearModelFit[{{x1,y1},{x2,y2},…},form,{β1,…},x]

构建公式为 form 的非线性模型，使用自由参数 βi 拟合每个 xi 的 yi.

NonlinearModelFit[data,form,params,{x1,…}]

构建一个非线性模型，其中 form 与变量 xk 相关.

NonlinearModelFit[data,{form,cons},params,{x1,…}]

在参数约束 cons 下构建一个非线性模型.

更多信息和选项

  • NonlinearModelFit 尝试使用具有自由参数的普通的数学公式模拟输入数据.
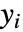  • NonlinearModelFit 给出形为 的非线性模型，假设原始的 服从均值为 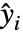和具有常见标准差的独立正态分布.
  • NonlinearModelFit 返回一个符号 FittedModel 对象，表示构建的线性模型. 模型的属性可以从 model["property"] 得到.
  • NonlinearModelFit 在特定点 x1，… 的最佳拟合函数的值可以从 model[x1,…] 得到.
  • NonlinearModelFit[data,form,pars,vars] 得到的最佳拟合函数和 FindFit[data,form,pars,vars] 的结果相同.
  • NonlinearModelFit[data,form,{{β1,val1},…},vars] 从 {β1->val1,…} 开始搜索拟合值.
  • data 的可能的形式为：
  • {y1,y2,…}与形式 {{1,y1},{2,y2},…} 等价
    {{x11,x12,…,y1},…}独立值 xij 列表和响应 yi
    {{x11,x12,…}y1,…}输入值和响应构成的规则列表
    {{x11,x12,…},…}{y1,y2,…}输入值列表和响应构成的规则
    {{x11,…,y1,…},…}n拟合矩阵的第 n 列
  • 在多元数据的情况下，如 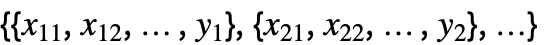{{x_(11),x_(12),... ,y_(1)},{x_(21),x_(22),... ,y_(2)},...}，坐标 xi1、xi2、… 的数量应等于变量 xi 的数量.
  • 数据点可以是近似实数. 不确定性可以用 Around 来指定.
    • 选项
  • NonlinearModelFit 采用下列选项：
  • AccuracyGoalAutomatic搜索的准确度
    ConfidenceLevel 95/100参数和预测的置信度
    EvaluationMonitorNone当计算 form 时，需要计算的表达式
    GradientAutomaticform 的梯度分量列表
    MaxIterationsAutomatic使用迭代的最大数量
    Method Automatic使用的方法
    PrecisionGoalAutomatic搜索的精度
    StepMonitorNone当运用步长时，计算的表达式
    VarianceEstimatorFunction Automatic估计误差方差的值或函数
    Weights Automatic数据元素的权
    WorkingPrecision Automatic内部计算的精度
  • 在 ConfidenceLevel->p 下，对参数和预测区间计算概率-p 的置信区间.
  • 在设置 Weights->{w1,w2,…} 下，yi 的误差方差被假定为与 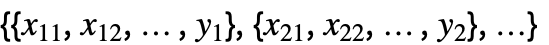成比例.
  • 在设置 Weights->Automatic 下，如果数据包含精确值，则权重将设置为 1. 如果数据包含 Around 值，则权重将设置为 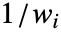，其中 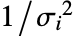为总响应方差.
  • 总响应方差 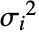是初始响应方差 Δyi2 和独立值方差 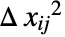的函数.
  • 不确定性 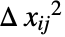通过使用 AroundReplace 在模型中传播，并将得到的方差加到响应方差 Δyi2. 根据 Fasano 和 Vio 方法，FindRoot 函数在内部用于寻找自洽解.
  • 设置 VarianceEstimatorFunction->f，普通的方差通过 f[res,w] 估计，其中 res={y1-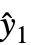,y2-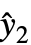,…} 是残差列表， w 是权列表.
  • 用 VarianceEstimatorFunction->(1&) 和 Weights->{1/Δy12,1/Δy22,…}， Δyi 视为已知的测量不确定度 yi，参数标准误差实际上仅从权计算.
  • Method 的可能设置包括：
  • "ConjugateGradient"非线性共轭梯度
    "Gradient"梯度递减
    "LevenbergMarquardt"最小二乘法的高斯-牛顿方法
    "Newton"牛顿方法
    "QuasiNewton"拟牛顿 BFGS 法
    "InteriorPoint"内点法
    "NMinimize"使用 NMinimize 进行最优化
    Automatic自动默认方法
  • 可以用形式 Method->{…,opts} 给出其他方法子选项.
  • Method 选项可以采用教程“非约束最优化：局部极小化方法”中指定的任何局部优化方法. »
  • 可用 "NMinimize" 方法的子方法指定任何全局优化方法. 可以在“约束全局最优化的数值算法”教程中找到这些方法. »
    • 属性
  • 对于约束模型，基于近似正态的属性可能不是有效的. 当计算这样的变量时，同时也产生一个警告信息.
  • 用 model["property"] 得到的数据和拟合函数的属性包括：
  • "BestFit"拟合函数
    "BestFitParameters"参数估计
    "Data"输入数据
    "Function"最佳拟合的纯函数
    "Response"输入数据中的响应值
    "Weights"用于拟合数据的权值
  • 残差类型包括：
  • "FitResiduals"具体响应和预测响应的差异
    "StandardizedResiduals"通过除以每个残差的标准误差的拟合残差
    "StudentizedResiduals"通过除以单个删除误差估计的拟合残差
  • 与平方误差和相关的属性包括：
  • "ANOVA"方差数据分析
    "EstimatedVariance"误差方差的估计
  • 参数估计的属性包括：
  • "CorrelationMatrix"渐近线的参数相关矩阵
    "CovarianceMatrix"渐近线的参数协方差矩阵
    "ParameterEstimates"拟合参数信息表
    "ParameterBias"参数估计的估计偏差
    "ParameterConfidenceRegion"椭圆参数的置信区域
  • 曲率诊断的属性包括：
  • "CurvatureConfidenceRegion"曲率诊断的置信区间
    "FitCurvature"拟合曲率信息表
    "MaxIntrinsicCurvature"最大内在曲率的测量
    "MaxParameterEffectsCurvature"最大参数效果曲率的测量
  • 影响度量的相关属性包括：
  • "HatDiagonal"帽子矩阵的对角元素
    "SingleDeletionVariances"方差估计列表，忽略第 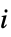个数据点
  • 预测值属性包括：
  • "MeanPredictionBands"均值预测的置信带
    "MeanPredictions"均值预测的置信区间
    "PredictedResponse"数据的拟合值
    "SinglePredictionBands"基于单个观察值的置信带
    "SinglePredictions"单个观察值预测响应的置信区间
  • 拟合优度度量的属性包括：
  • "AdjustedRSquared"模型参数数量的 调整
    "AIC"Akaike 信息标准
    "AICc"有穷样本校正 AIC
    "BIC"贝叶斯信息标准
    "RSquared"决定系数

范例

打开所有单元关闭所有单元

基本范例  (1)

拟合某些数据的一个非线性模型：

查看模型的函数形式：

在某个点的计算：

可视化显示拟合函数：

提取并绘制残差：

范围  (15)

数据  (7)

拟合单变量的模型，假设增大的整数独立数值：

拟合不止一个变量的模型：

拟合规则列表：

拟合输入值和响应构成的规则：

指定一列数据作为响应：

当参数远离缺省值 1，给出初值：

使用默认起始值，该模型接近 0：

得到一个非线性模型的现有参数的列表：

属性  (8)

数据 & 拟合函数  (1)

拟合一个非线性模型：

提取原数据：

得到并绘制最佳拟合：

得到拟合函数，作为一个纯函数：

残差  (1)

检查拟合的残差：

可视化显示原残差：

在图形中显示尺度残差：

绘制标准化残差和 Studentized 残差的绝对误差：

平方和  (1)

拟合某些数据的一个非线性模型：

提取估计误差方差：

分析方差表：

得到表格中列平方和：

参数估计诊断  (1)

得到参数信息的一个格式化表：

提取 -统计值的列：

曲率诊断  (1)

拟合某些数据的一个非线性模型：

拟合模型的曲率测量表：

提取数值的列表：

提取最大影响曲率参数值：

影响度量  (1)

拟合包含极值的一个非线性模型：

用单个删除方差，检测消去每个点的误差方差的影响：

检测帽子矩阵的对角元素，估计拟合每个点的影响：

预测值  (1)

拟合一个非线性模型：

绘制与估计值相应预测值：

得到矩阵和单个预测置信区间的表格：

得到简单预测区间：

提取 99% 均值预测带：

拟合优度度量  (1)

获取非线性模型的拟合优度测量表：

推广和延伸  (2)

拟合一个数值运算定义的模型：

使用 ParametricNDSolveValue 缓存微分方程的解，使计算速度更快：

在模型的函数形式上执行其它的数学操作：

符号积分和数值积分：

求出一个预期值，得到模型的一个特定值：

选项  (10)

ConfidenceLevel  (1)

缺省给出 95% 置信区间：

用 99% 的置信区间：

在 FittedModel 中设置级别为 90%：

Method  (3)

使用默认方法来最小化最小二乘目标函数：

使用牛顿法进行优化：

配置牛顿算法步长控制方式：

使用有约束条件的内点法：

使用 NMinimize 的全局优化方法进行更仔细的搜索：

使用子方法 "RandomSearch"：

指定 "RandomSearch" 算法的初始搜索点的数量：

VarianceEstimatorFunction  (1)

用缺省的无偏差估计：

假设一个已知的误差方差：

通过均值平方误差估计方差：

Weights  (4)

用等权拟合一个模型：

给出某些数据点的明确权：

使用 Around 值为数据点赋予不同的权重：

找到用于解释数据不确定性的权值：

在独立值和响应中使用 Around 值：

在某些情况下，处理自变量不确定性的求根算法在使用标准选项设置时可能不会收敛：

使用 FixedPoint 算法，设置较低的阻尼因子和较高的 MaxIterations 来达到收敛：

WorkingPrecision  (1)

用 WorkingPrecision 在参数估计中得到更高的精度：

得到拟合函数：

在拟合后，化简属性计算中的精度：

应用  (1)

模仿某些数据：

拟合一个非线性模型：

得到并可视化 90% 置信带：

得到 95%、99% 和 99.9% 置信带：

可视化不同水平下的置信带：

属性和关系  (5)

假设正态分布误差，NonlinearModelFit 拟合线性和非线性模型：

假设正态分布误差，LinearModelFit 拟合线性模型：

FindFit 和 NonlinearModelFit 拟合等价模型：

NonlinearModelFit 允许提取拟合的其它信息：

NonlinearModelFit 假设正态分布响应：

LogitModelFit 假设二项分布响应：

相等的拟合：

对于 ProbitModelFit 是相同的：

NonlinearModelFit 会使用一个 TimeSeries 的时间戳作为变量：

重新缩放时间戳并使其合适：

求出适合的值：

NonlinearModelFit 在多路径 TemporalData 上顺向操作：

可能存在的问题  (3)

在无约束模型下，分配的假设：

的系数区间包含违背约束的点：

NonlinearModelFit 中的决定系数 使用未校正数据计算：

决定系数：

使用残差和数据直接计算：

有时候 使用中心化数据定义：

拟合跨越多个数量级的数据：

乍一看，指数拟合可能是正确的：

但在对数尺度上显示出明显的偏差：

可以通过使用与方差成反比的权重来解决：

Wolfram Research (2008)，NonlinearModelFit，Wolfram 语言函数，https://reference.wolfram.com/language/ref/NonlinearModelFit.html.

文本

Wolfram Research (2008)，NonlinearModelFit，Wolfram 语言函数，https://reference.wolfram.com/language/ref/NonlinearModelFit.html.

CMS

Wolfram 语言. 2008. "NonlinearModelFit." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/NonlinearModelFit.html.

APA

Wolfram 语言. (2008). NonlinearModelFit. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/NonlinearModelFit.html 年

BibTeX

@misc{reference.wolfram_2024_nonlinearmodelfit, author="Wolfram Research", title="{NonlinearModelFit}", year="2008", howpublished="\url{https://reference.wolfram.com/language/ref/NonlinearModelFit.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_nonlinearmodelfit, organization={Wolfram Research}, title={NonlinearModelFit}, year={2008}, url={https://reference.wolfram.com/language/ref/NonlinearModelFit.html}, note=[Accessed: 21-November-2024 ]}