OrnsteinUhlenbeckProcess[μ,σ,θ]
表示稳态 Ornstein–Uhlenbeck 过程,其中长期均值为 μ,波动率为 ![]() ,均值回归速度 θ.
,均值回归速度 θ.
OrnsteinUhlenbeckProcess[μ,σ,θ,x0]
表示一个 Ornstein–Uhlenbeck 过程,其中初始条件为 x0.


OrnsteinUhlenbeckProcess
OrnsteinUhlenbeckProcess[μ,σ,θ]
表示稳态 Ornstein–Uhlenbeck 过程,其中长期均值为 μ,波动率为 ![]() ,均值回归速度 θ.
,均值回归速度 θ.
OrnsteinUhlenbeckProcess[μ,σ,θ,x0]
表示一个 Ornstein–Uhlenbeck 过程,其中初始条件为 x0.
更多信息

- OrnsteinUhlenbeckProcess 是一个连续时间和连续状态随机过程.
- OrnsteinUhlenbeckProcess 也被称为 Vasicek 模型.
- Ornstein–Uhlenbeck 过程的状态
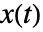 满足 Ito 微分方程
满足 Ito 微分方程 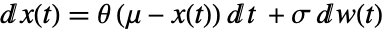 ,其中
,其中 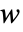 服从标准 WienerProcess[].
服从标准 WienerProcess[]. - OrnsteinUhlenbeckProcess[μ,σ,θ] 的初始值是随机的,并且服从 NormalDistribution[μ,σ/
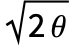 ].
]. - 时间 t 处的 OrnsteinUhlenbeckProcess[μ,σ,θ] 服从 NormalDistribution[μ,σ/
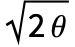 ].
]. - 时间 t 处的 OrnsteinUhlenbeckProcess[μ,σ,θ,x0] 服从 NormalDistribution[x0 exp(-θ t)+μ(1-exp(-θ t)),
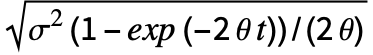 ].
]. - OrnsteinUhlenbeckProcess 允许 μ 和 x0 是任意实数,并且 σ 和 θ 是任意正实数.
- OrnsteinUhlenbeckProcess 可以用于诸如 Mean、PDF、Probability 和 RandomFunction 等函数.
范例
打开所有单元 关闭所有单元范围 (12)
基本用途 (7)
过程切片属性 (5)
属性和关系 (9)
从随机数开始的 OrnsteinUhlenbeckProcess 是弱稳态的:
Ornstein–Uhlenbeck 过程具有定义良好的 StationaryDistribution:
Ornstein–Uhlenbeck 过程不具有独立的增量:
具有固定初始条件的 Ornstein–Uhlenbeck 过程是一个特殊的 ItoProcess:
Ornstein–Uhlenbeck 过程是随机微分方程 ![]() 的解:
的解:
具有三个参数的 Ornstein–Uhlenbeck 是均值遍历的:
整数时间处的 Ornstein–Uhlenbeck 过程的表现与一阶 ARProcess 类似:
创建矩方程用来求 ARProcess 的参数:
创建 ARProcess:
文本
Wolfram Research (2012),OrnsteinUhlenbeckProcess,Wolfram 语言函数,https://reference.wolfram.com/language/ref/OrnsteinUhlenbeckProcess.html.
CMS
Wolfram 语言. 2012. "OrnsteinUhlenbeckProcess." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/OrnsteinUhlenbeckProcess.html.
APA
Wolfram 语言. (2012). OrnsteinUhlenbeckProcess. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/OrnsteinUhlenbeckProcess.html 年
BibTeX
@misc{reference.wolfram_2025_ornsteinuhlenbeckprocess, author="Wolfram Research", title="{OrnsteinUhlenbeckProcess}", year="2012", howpublished="\url{https://reference.wolfram.com/language/ref/OrnsteinUhlenbeckProcess.html}", note=[Accessed: 10-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_ornsteinuhlenbeckprocess, organization={Wolfram Research}, title={OrnsteinUhlenbeckProcess}, year={2012}, url={https://reference.wolfram.com/language/ref/OrnsteinUhlenbeckProcess.html}, note=[Accessed: 10-February-2026]}