Orthogonalize
Orthogonalize[{v1,v2,…}]
对正交化向量 vi,给出标准正交基.
Orthogonalize[{e1,e2,…},f]
给出通过关于内积函数 f 正交化元素 ei 得到的标准正交基.
更多信息和选项

- Orthogonalize[{v1,v2,…}] 用普通的标量积
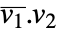 作为内积.
作为内积. - Orthogonalize 的输出通常包括和输入相同数目的向量. 如果一些输入向量不是线性无关的,输出则包含零向量.
- 输出的所有非零向量被归一化为单位向量.
- 内积函数 f 被应用于 ei 的各种线性组合.
- ei 可以为任意使 f 产生实数结果的表达式. »
- Orthogonalize[{v1,v2,…},Dot] 认为 vi 的所有元素是实数. »
- Orthogonalize 默认生成一个 Gram-Schmidt(格莱姆-施密特)正交基.
- Method 选项的设置可以获得其它类型的基. 可以选择的设置包括:"GramSchmidt"、"ModifiedGramSchmidt"、"Reorthogonalization" 和 "Householder".
- Orthogonalize[list,Tolerance->t] 将相对范数小于 t 的元素设为零.
范例
打开所有单元关闭所有单元范围 (13)
特殊矩阵 (4)
选项 (3)
应用 (12)
几何学 (3)
最小二乘和曲线拟合 (3)
如果线性系统 ![]() 无解,最好的近似解是最小二乘解. 这就是
无解,最好的近似解是最小二乘解. 这就是 ![]() 的解,其中
的解,其中 ![]() 是
是 ![]() 在
在 ![]() 的列空间上的正交投影. 考虑以下
的列空间上的正交投影. 考虑以下 ![]() 和
和 ![]() :
:
使用 LeastSquares 确认结果:
Orthogonalize 可用于找到数据的最佳拟合曲线. 考虑以下数据:
使用 Fit 验证系数;
使用 Fit 验证系数:
矩阵分解 (2)
求以下矩阵 ![]() 的列空间的正交基,然后使用该基找到
的列空间的正交基,然后使用该基找到 ![]() 的 QR 分解:
的 QR 分解:
将 Gram–Schmidt 应用于 ![]() 的列,然后将
的列,然后将 ![]() 定义为其列是那些向量的矩阵:
定义为其列是那些向量的矩阵:
与 QRDecomposition 给出的结果进行比较;与 ![]() 矩阵是相同的:
矩阵是相同的:
![]() 矩阵因转置而不同,因为 QRDecomposition 给出了行正交结果:
矩阵因转置而不同,因为 QRDecomposition 给出了行正交结果:
对于埃尔米特矩阵(更一般地,任何正规矩阵),特征向量是正交的,并且通常定义投影矩阵 ![]() ,其中
,其中 ![]() 是归一化的特征向量. 证明投影矩阵对一般向量的作用与将向量投影到以下矩阵
是归一化的特征向量. 证明投影矩阵对一般向量的作用与将向量投影到以下矩阵 ![]() 的特征空间上的作用相同:
的特征空间上的作用相同:
使用 Orthogonalize 从 ![]() 创建一个正交基:
创建一个正交基:
通用内积和函数空间 (4)
注意 Dot 本身是与单位矩阵相关的内积:
傅立叶级数是在内积空间 ![]() 中正交基上的投影. 定义平方可积函数的标准内积:
中正交基上的投影. 定义平方可积函数的标准内积:
![]() 等于对应于 FourierParameters{0,1} 的对称傅立叶系数:
等于对应于 FourierParameters{0,1} 的对称傅立叶系数:
使用 FourierCoefficient 确认:
使用 FourierSeries 确认结果:
LegendreP 定义关于内积 ![]() 的正交多项式族. 将
的正交多项式族. 将 ![]() 从 0 到 4 的多项式
从 0 到 4 的多项式 ![]() 正交化,以计算前 5 个勒让德多项式的标量倍数:
正交化,以计算前 5 个勒让德多项式的标量倍数:
HermiteH 定义关于内积 ![]() 的正交多项式族. 将未归一化的 Gram–Schmidt 过程应用于
的正交多项式族. 将未归一化的 Gram–Schmidt 过程应用于 ![]() 从 0 到 4 的多项式
从 0 到 4 的多项式 ![]() ,以计算前 5 个埃尔米特多项式的标量倍数:
,以计算前 5 个埃尔米特多项式的标量倍数:
属性和关系 (9)
如果输入向量不是线性独立的,则用零向量填充结果以达到匹配的长度:
如果 ![]() 是 Orthogonalize[vecs] 的结果,则
是 Orthogonalize[vecs] 的结果,则 ![]() 是一个对角矩阵:
是一个对角矩阵:
使用默认方法的情况下,基的第一个元素通常是第一个向量的倍数:
Orthogonalize 可以通过重复应用 Projection 和 Normalize 来实现:
Orthogonalize[m] 与 QRDecomposition[Transpose[m]] 相关:
文本
Wolfram Research (2007),Orthogonalize,Wolfram 语言函数,https://reference.wolfram.com/language/ref/Orthogonalize.html.
CMS
Wolfram 语言. 2007. "Orthogonalize." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/Orthogonalize.html.
APA
Wolfram 语言. (2007). Orthogonalize. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/Orthogonalize.html 年