PearsonChiSquareTest

PearsonChiSquareTest[data]

ピアソンのカイ二乗検定を使い，data が正規分布に従っているかどうかを調べる．

PearsonChiSquareTest[data,dist]

ピアソンのカイ二乗検定を使い，data が dist に従った分布かどうかを調べる．

PearsonChiSquareTest[data,dist,"property"]

"property"の値を返す．

詳細とオプション

  • PearsonChiSquareTestは data が分布 dist に従う母集団から引き出されたという帰無仮説 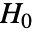とそうではないという対立仮説 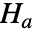でピアソンのカイ二乗適合度検定を行う．
  • デフォルトで，確率値つまり 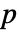値が返される．
  • 小さい 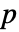値は data が dist から来ている可能性が低いことを示す．
  • dist は，記号および数値の母数，またはデータ集合，を持つ任意の記号分布でよい．
  • data は一変量{x1,x2,…}でも多変量{{x1,y1,…},{x2,y2,…},…}でもよい．
  • ピアソンのカイ二乗検定は，事実上，data のヒストグラムと dist に基づいた理論的なヒストグラムを比較する．dist における確率が等しくなるようにビンが選ばれる． »
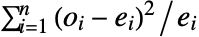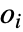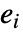  • 一変量データについては，検定統計は で与えられる．ただし，と はそれぞれ 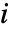番目のヒストグラムビンの観察された数および期待される数である．
  • 多変量検定では一変量限界 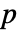値の総和が使われる．総和は 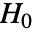のもとでUniformSumDistributionに従うものと想定される．
  • PearsonChiSquareTest[data,dist,"HypothesisTestData"]はHypothesisTestDataオブジェクト htd を返す．これは htd["property"]として追加的な検定結果と特性の抽出に使うことができる．
  • PearsonChiSquareTest[data,dist,"property"]を使って直接"property"を与えることができる．
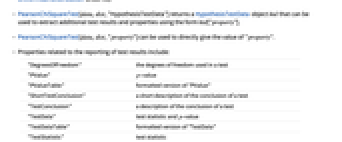
  • 検定結果のレポートに関連する特性
  • "DegreesOfFreedom"検定に使われる自由度
    "PValue" 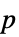値
    "PValueTable""PValue"のフォーマットされたバージョン
    "ShortTestConclusion"検定結果の簡単な説明
    "TestConclusion"検定結果の説明
    "TestData"検定統計と 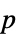値
    "TestDataTable""TestData"のフォーマットされたバージョン
    "TestStatistic"検定統計
    "TestStatisticTable""TestStatistic"のフォーマットされたバージョン
  • 次の特性はどの検定が行われているかに依存しない．
  • データ分布に関連する特性
  • "FittedDistribution"データのフィットした分布
    "FittedDistributionParameters"データの分布母数
  • 使用可能なオプション
  • Method Automatic 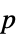値を計算するメソッド
    SignificanceLevel0.05診断とレポートのための切捨て
  • 適合度検定では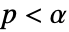， のときにのみ 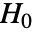が棄却されるような切捨て 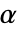が選択される．特性"TestConclusion"および"ShortTestConclusion"で使われる 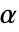の値はSignificanceLevelオプションで制御される．デフォルトで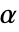， は0.05に設定されている．
  • Method->"MonteCarlo"の設定では，入力 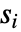と同じ長さの 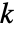個のデータ集合が 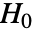のもとにフィットされた分布を使って生成される．次に，PearsonChiSquareTest[si,dist,"TestStatistic"]からのEmpiricalDistributionを使って 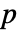値が推定される．

例題

すべて開くすべて閉じる

例  (4)

正規性についてピアソンのカイ二乗検定を行う：

あるデータが特定の分布にフィットするかどうかの検定を行う：

2つのデータ集合の分布を比較する：

ピアソンのカイ二乗検定から検定統計を抽出する：

スコープ  (9)

検定  (6)

正規性についてピアソン(Pearson)のカイ二乗検定を行う：

正規データの 値は，非正規データの 値と比べて大きい：

特定の分布に対して適合度検定を行う：

2つのデータ集合の分布を比べる：

2つのデータ集合は同じ分布に従わない：

多変量正規性について検定する：

任意多変量分布について適合度検定を行う：

繰り返し特性を抽出するためにHypothesisTestDataオブジェクトを作成する：

抽出に使用できる特性：

レポート  (3)

ピアソンのカイ二乗検定の結果を表にする：

完全な検定表：

値の表：

検定統計：

カスタマイズされたレポート用にピアソンのカイ二乗検定表から項目を取り出す：

"ShortTestConclusion"と"TestConclusion"を使って検定の結論をレポートする：

有意水準が異なると，結論も異なることがある：

オプション  (3)

Method  (3)

計算式またはモンテカルロ法に基づくメソッドを使う：

モンテカルロ法に基づくメソッドで使うサンプル数を設定する：

モンテカルロ推定は，サンプルを増やすと，真の 値に収束する：

モンテカルロ法に基づくメソッドで使われるランダムなシードを設定する：

シードは生成器の状態に影響を与え，結果の 値にもいくらか影響を与える：

アプリケーション  (2)

ピアソンのカイ二乗検定の検出力曲線：

近似検出力曲線を可視化する：

基礎となる分布がUniformDistribution[{-4,4}]であり，検定サイズが0.05，サンプルサイズが12である場合に，ピアソンのカイ二乗検定の検出力を推定する：

ある都市における30日間の自動車事故の数が記録された．市議会は都市内の制限速度を下げることを計画しており，後で比較するときの基準値として事故率のモデルを希望している：

数のデータはPoissonDistributionでうまくモデル化されることが多い：

都市が制限速度を下げた後でさらに30日間データを集めたとする．制限速度を下げる前と後の分布を比較する：

分布はかなり違う：

特性と関係  (10)

デフォルトで一変量データはNormalDistributionと比べられる：

母数はデータから推定されている：

多変量データは，デフォルトでMultinormalDistributionと比べられる：

検定分布の母数は，指定されない場合にはデータから推測される：

指定された母数は推測されない：

最尤推定値は，検定分布の指定されていない母数に使われる：

PearsonChiSquareTestは事実上観測値のヒストグラムと推定値のヒストグラムを比較する：

データは，において確率が等しい約個のビンに入れられる：

において各ビンには同じ数の点が含まれる：

が真である場合と偽である場合のそれぞれの観測値のヒストグラム：

自由度は非空のビンから1引いた数に等しい：

データから推測される母数それぞれについて，1つの自由度が削除される：

母数が未知の場合，PearsonChiSquareTestは自由度を修正する：

母数が指定されると，修正は適用されない：

フィットされた分布は前と同じであるが，自由度と 値は修正される：

ピアソンのカイ二乗統計は，において漸近的にChiSquareDistributionに従う：

独立周辺密度が多変量の適合度検定では仮定される：

独立性が仮定されると，検定統計は同一である：

ピアソンのカイ二乗検定は，入力がTimeSeries:のときにのみ値に使うことができる：

おもしろい例題  (1)

帰無仮説 が真であるときの統計量を計算する：

特定の対立仮説による検定統計：

検定統計の分布を比較する：

Wolfram Research (2010), PearsonChiSquareTest, Wolfram言語関数， https://reference.wolfram.com/language/ref/PearsonChiSquareTest.html.

テキスト

Wolfram Research (2010), PearsonChiSquareTest, Wolfram言語関数， https://reference.wolfram.com/language/ref/PearsonChiSquareTest.html.

CMS

Wolfram Language. 2010. "PearsonChiSquareTest." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/PearsonChiSquareTest.html.

APA

Wolfram Language. (2010). PearsonChiSquareTest. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/PearsonChiSquareTest.html

BibTeX

@misc{reference.wolfram_2024_pearsonchisquaretest, author="Wolfram Research", title="{PearsonChiSquareTest}", year="2010", howpublished="\url{https://reference.wolfram.com/language/ref/PearsonChiSquareTest.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_pearsonchisquaretest, organization={Wolfram Research}, title={PearsonChiSquareTest}, year={2010}, url={https://reference.wolfram.com/language/ref/PearsonChiSquareTest.html}, note=[Accessed: 21-November-2024 ]}