Polygon

Polygon[{p1,p2,…}]

点 piを持つ，塗り潰された多角形を表す．

Polygon[{p1,…,pn}{{q1,…,qm},…}]

穴{q1,…,qm},…がある多角形を表す．

Polygon[{poly1,poly2,…}]

多角形 polyiの集合を表す．

Polygon[{p1,…,pn},data]

data 中の整数 i として与えられている座標を piと解釈すべき多角形を表す．

詳細とオプション

  • Polygonは，幾何領域としてあるいはグラフィックスプリミティブとして使うことができる．
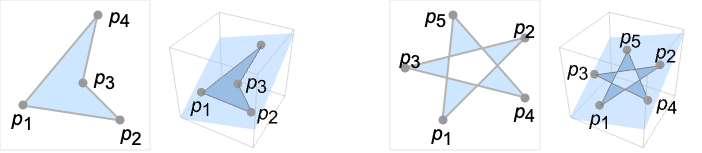
  • Polygon[{p1,…,pn}]は，線分{p1,p2},…,{pn-1,pn}と{pn,p1}で閉じた曲線内のすべての点を表す平面領域である．
  • 平面上のある点から任意の方向に向かう半直線が境界線と奇数回交差するなら，その点は多角形の要素である．
  • Polygon[{p1,…,pn}{{q1,…,qm},…}]は，外側多角形Polygon[{p1,…,pn}]と1つあるいは複数の内側多角形Polygon[{q1,…,qm}],…からなる穴のある多角形を指定する．
  • ある点が外側多角形には含まれるが任意の内側多角形には含まれないなら，その点は多角形の要素である．
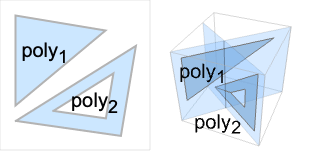
  • Polygon[{poly1,poly2,…}]は，穴があるまたは穴がない多角形 polyiの集合で，幾何学計算では polyiの和集合として扱われる．
  • Polygon[{p1,…,pn},data]は，事実上，data 中の座標として現れる整数 i を対応する piで置換する．
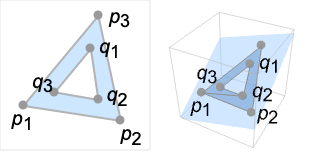
  • Polygon[{p1,…,pn},{b1,…,bn}]多角形の境界点{pb1,…,pbk}
    Polygon[{p1,…,pn},{{o1,…,ok}{{i1,…,il},…}]外側多角形の境界点{po1,…,pok}と内側多角形の境界点{pi1,…,pil}等
    Polygon[{p1,…,pn},{{b1,…,bn},{o1,…,ok}{{i1,…,il},…},…}]複数の多角形の集合
  • 点 piは，幾何領域として任意の埋込み次元を持つことができるが，すべてが1つの平面上で同じ埋込み次元を持たなければならない．
  • グラフィックスでは，点 piは，Scaled，Offset，ImageScaled，Dynamicの各式でよい．
  • グラフィックスの描画は，FaceForm，EdgeForm，Texture，Specularity，Opacity，色の各指示子の影響を受ける．
  • FaceForm[front,back]を使って3Dにおける多面体の表と裏に異なるスタイルを指定することができる．表は右辺規則と最初の3点の方向で定義される．
  • 次は，グラフィックスで使用可能なオプションおよび設定値である．
  • VertexColors Automatic補間される頂点の色
    VertexNormals Automatic陰影付けのための有効な頂点法線
    VertexTextureCoordinates Noneテクスチャのための座標
  • Polygonは，GeometricSceneの記号の点と一緒に使うことができる．

例題

すべて開くすべて閉じる

例  (2)

多角形：

そのグラフィックス画像：

その面積：

さまざまにスタイル付けされた3D多角形：

スコープ  (21)

グラフィックス  (11)

指定  (2)

一群の多角形：

複数の頂点を持つ多角形：

スタイリング  (6)

色指示子で多角形の面の色を指定する：

Textureを使って多角形の面に使用するテクスチャが指定できる：

Textureは異なるOpacityで使うことができる：

Textureは異なるLightingで使うことができる：

FaceFormおよびEdgeFormを使って内部と境界のスタイルが指定できる：

三次元では，FaceFormを使って表面と裏面に異なる特性が指定できる：

FaceFormを使って3Dの外側と内側に別々のテクスチャを設定する：

VertexColorsを使って頂点における色が指定できる：

3Dの多角形については，法線はVertexNormalsを使って頂点で指定することができる：

座標  (3)

スケールされた(Scaled)座標を使う：

2Dで画像がスケールされた(ImageScaled)座標を使う：

2DでOffset座標を使う：

領域  (10)

埋込み次元：

幾何次元：

点の帰属判定：

点の帰属条件を求める：

面積：

重心：

点からの距離：

これをプロットする：

点からの符号付き距離：

これをプロットする：

領域内の最近点：

最近点：

多角形は有界である：

領域を求める：

多角形上でIntegrate：

多角形上で最適化する：

多角形内で方程式を解く：

オプション  (7)

VertexColors  (2)

頂点に色がある多角形：

3D多角形の頂点の色を指定する：

VertexNormals  (1)

辺のベクトルのクロス積を使って法線ベクトルを計算する：

{1,-1,1}の方向を指している法線を持つ三角形：

法線を変更すると陰影付けに影響する：

VertexTextureCoordinates  (4)

テクスチャマップされた多角形：

2D多角形のテクスチャマッピング：

3D多面体のテクスチャマッピング：

統一されていないテクスチャ座標値を使ってテクスチャを繰り返す：

VertexColorsはテクスチャマッピングに優先する：

アプリケーション  (3)

個の頂点を持つ多角形を定義する：

正多角形：

星形多角形：

正六角形を定義する：

正六角形を敷き詰める：

PolyhedronDataから多角形面を得る：

各面を重心について縮小する：

特性と関係  (4)

GraphicsComplexは，多くの頂点を共有する多角形を効率的に生成する方法を提供する：

Normalをグラフィックス複合体に適用すると通常の多角形が生成できる：

PolygonはTriangleを一般化したものである：

PolygonはRectangleを一般化したものである：

3つの頂点があるSimplexはPolygonの特殊ケースである：

2から始まる任意次元で：

考えられる問題  (3)

三次元では，頂点が平面上にない場合，多角形の三角形分割は予測できない：

退化した多角形は有効な幾何領域ではない：

アンチエイリアス処理の結果として個々の多角形間に継ぎ目が現れることがある：

単一の多角形オブジェクトを使うことで継ぎ目を避けることができる：

おもしろい例題  (3)

ランダムな三角形の集合：

デジタル花弁：

回転する星：

Wolfram Research (1988), Polygon, Wolfram言語関数， https://reference.wolfram.com/language/ref/Polygon.html （2019年に更新）.

テキスト

Wolfram Research (1988), Polygon, Wolfram言語関数， https://reference.wolfram.com/language/ref/Polygon.html （2019年に更新）.

CMS

Wolfram Language. 1988. "Polygon." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2019. https://reference.wolfram.com/language/ref/Polygon.html.

APA

Wolfram Language. (1988). Polygon. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Polygon.html

BibTeX

@misc{reference.wolfram_2024_polygon, author="Wolfram Research", title="{Polygon}", year="2019", howpublished="\url{https://reference.wolfram.com/language/ref/Polygon.html}", note=[Accessed: 15-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_polygon, organization={Wolfram Research}, title={Polygon}, year={2019}, url={https://reference.wolfram.com/language/ref/Polygon.html}, note=[Accessed: 15-November-2024 ]}