QnDispersion
QnDispersion[list]
list 中の要素の ![]() 統計量を与える.
統計量を与える.
QnDispersion[list,c]
尺度係数 c を使って ![]() 統計量を与える.
統計量を与える.
詳細とオプション

- QnDispersionはロバストな分散測度である.
- QnDispersionは,その統計量がペアごとの絶対差に基づく,順序に基づいた推定器である.この統計には位置推定は必要ない.
- リスト{x1,x2,…,xn}についての
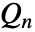 統計量の値は,集合{xi– xj,i<j}の第1四分位量に尺度係数 c を掛けたもので与えられる.
統計量の値は,集合{xi– xj,i<j}の第1四分位量に尺度係数 c を掛けたもので与えられる. - c が指定されていない場合は,
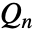 統計量が正規分布に従うデータについての尺度母数の一定した推定器となるように,尺度係数
統計量が正規分布に従うデータについての尺度母数の一定した推定器となるように,尺度係数  が適用される.また,サンプル量が少ない場合に推定器に偏りが生まれないように,デフォルトで有限サンプル修正が使われる.
が適用される.また,サンプル量が少ない場合に推定器に偏りが生まれないように,デフォルトで有限サンプル修正が使われる. - QnDispersion[{{x1,y1,…},{x2,y2,…},…}]は{QnDispersion[{x1,x2,…}],QnDispersion[{y1,y2,…}],…}を与える.
- QnDispersionはMethodオプションをサポートする.次は,指定可能な明示的設定である.
-
"FiniteSample" 有限サンプル修正を使う(デフォルト) "None" 修正は行わない - 尺度係数 c が入力で指定されている場合は,オプションMethodは無視される.
例題
すべて開くすべて閉じる例 (4)
スコープ (8)
厳密な入力は,尺度係数が厳密である場合は厳密な出力を与える:
尺度母数が異なるQnDispersion:
行列についてのQnDispersionは列ごとの推定を与える:
大きい配列のQnDispersion:
TimeSeriesのQnDispersionを求める:
QnDispersionは単位付き数量を含むデータに使うことができる:
日付のQnDispersionを計算する:
時間のQnDispersionを計算する:
アプリケーション (6)
特性と関係 (2)
QnDispersionは,その統計量がペアごとの絶対差に基づく,順序に基づいた分散推定器である:
差の中から正の値を取り出し,RankedMinを使って順序統計を計算する:
尺度係数が1に等しいQnDispersionと比較する:
赤い線が![]() 統計量の値を示している,ペアごとの差のHistogram:
統計量の値を示している,ペアごとの差のHistogram:
QnDispersion,SnDispersion,StandardDeviationは,NormalDistributionの尺度母数の推定器である:
推定された結果を使ってStandardDeviationについての相対効率を計算する:
テキスト
Wolfram Research (2017), QnDispersion, Wolfram言語関数, https://reference.wolfram.com/language/ref/QnDispersion.html (2024年に更新).
CMS
Wolfram Language. 2017. "QnDispersion." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2024. https://reference.wolfram.com/language/ref/QnDispersion.html.
APA
Wolfram Language. (2017). QnDispersion. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/QnDispersion.html