WOLFRAM

Wolfram 语言与系统参考资料中心

QnDispersion[list]

给出 list 中元素的 统计量.

QnDispersion[list,c]

给出缩放因子为 c 时的 统计量.

更多信息和选项
Details and Options Details and Options
范例  
基本范例  
范围  
选项  
Method  
应用  
属性和关系  
参见
相关指南
历史
按以下格式引用：

QnDispersion

QnDispersion[list]

给出 list 中元素的 统计量.

QnDispersion[list,c]

给出缩放因子为 c 时的 统计量.

更多信息和选项

  • QnDispersion 是稳健的分散度度量.
  • QnDispersion 是基于排序结果的估计量，其统计基于数据对间的绝对差值. 该统计量不要求位置估计.
  • 对于列表 {x1,x2,…,xn}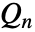， 统计量的值为集合 {xi– xj,i<j} 的第一四分位数乘以缩放因子 c.
  • 如果没有指定 c，则运用缩放因子 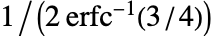来使得 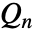统计量成为正态分布数据的尺度参数的相容估计量. 同时，在缺省情况下使用有限样本校正来纠正小样本对估计量造成的偏差.
  • QnDispersion[{{x1,y1,…},{x2,y2,…},…}] 给出 {QnDispersion[{x1,x2,…}],QnDispersion[{y1,y2,…}],…}.
  • QnDispersion 支持 Method 选项. 可以指定下列设置：
  • "FiniteSample"使用有限样本校正（缺省）
    "None"不使用校正
  • 如果输入中指定了缩放因子 c，则忽略选项 Method.

范例

打开所有单元 关闭所有单元

基本范例  (4)

列表的 QnDispersion：

Wolfram Language code: QnDispersion[{6.5, 3.8, 6.6, 5.7, 6.0, 6.4, 5.3}]

矩阵的列的 QnDispersion：

Wolfram Language code: QnDispersion[{{1., 2.}, {4., 8.}, {5., 3.}, {2., 15.}}]

缩放因子为 1 时列表的 QnDispersion：

Wolfram Language code: QnDispersion[{1, 2, 3, 2, 1}, 1]

日期列表的 QnDispersion：

Wolfram Language code: QnDispersion[{Yesterday, Today, Tomorrow}]

范围  (8)

当缩放因子是精确值时，精确输入给出精确输出：

Wolfram Language code: QnDispersion[{1, 20, 3, 4}, 1]
Wolfram Language code: QnDispersion[{Sqrt[2], E, Pi, Pi ^ 2, 1, 2, 3}, 2]

不同缩放参数情况下的 QnDispersion：

Wolfram Language code: QnDispersion[{1.2, 3.8, 4.2, -0.5, -5.2}, 3]
Wolfram Language code: QnDispersion[{1.2, 3.8, 4.2, -0.5, -5.2}, 4]

矩阵的 QnDispersion 按列给出估计：

Wolfram Language code: QnDispersion[RandomReal[1, {50, 3}]]

大型数组的 QnDispersion：

Wolfram Language code: QnDispersion[RandomReal[1, 10 ^ 6]]
Wolfram Language code: QnDispersion[RandomReal[1, {10 ^ 6, 2}]]

求 TimeSeries 的 QnDispersion：

Wolfram Language code: ts = TemporalData[TimeSeries, {{{3, 8, 4, 11, 9, 2}}, {{{1, 3, 5, 7, 8, 10}}}, 1, {"Continuous", 1}, {"Discrete", 1}, 1, {ResamplingMethod -> {"Interpolation", InterpolationOrder -> 1}}}, False, 10.1];
Wolfram Language code: QnDispersion[ts]

分散度只取决于值：

Wolfram Language code: QnDispersion[ts["Values"]]

可将 QnDispersion 用于含有量的数据：

Wolfram Language code: data = Quantity[RandomReal[1, 6], "Meters"]
Wolfram Language code: QnDispersion[data]

计算日期的 QnDispersion：

Wolfram Language code: dates = WolframLanguageData[All, "DateIntroduced"];
Wolfram Language code: DateHistogram[dates]
Wolfram Language code: QnDispersion[dates]
Wolfram Language code: UnitConvert[%, "Years"]

计算时间的 QnDispersion：

Wolfram Language code: RandomTime[3]
Wolfram Language code: QnDispersion[%]

以不同的时区规范给出的时间：

Wolfram Language code: {TimeObject[{12}, TimeZone -> 0], TimeObject[{12}, TimeZone -> 2], TimeObject[{12}, TimeZone -> "Asia/Tokyo"]}
Wolfram Language code: QnDispersion[%]

选项  (1)

Method  (1)

缺省情况下，使用有限样本校正：

Wolfram Language code: data = RandomVariate[NormalDistribution[0, 2], {10 ^ 4, 5}];
Wolfram Language code: Mean[QnDispersion /@ data]

不使用小样本校正：

Wolfram Language code: Mean[QnDispersion[#, Method -> "None"]& /@ data]

应用  (6)

在极值出现的情况下，计算分散度稳健估计值：

Wolfram Language code: QnDispersion[{3, 10, 10 ^ 6, 20, 5, 6}]

样本的标准方差受极值的影响很大：

Wolfram Language code: StandardDeviation[{3, 10, 10 ^ 6, 20, 5, 6}]//N

使用五年移动 分散度识别股票数据中的高波动周期：

Wolfram Language code: data = TemporalData[«4»];
Wolfram Language code: smooth = Sqrt[MovingMap[QnDispersion, data, {Quantity[5, "Year"]}]];
Wolfram Language code: DateListPlot[smooth]

计算随机过程中一组路径的切片的 分散度：

Wolfram Language code: data = RandomFunction[WienerProcess[], {0, 1, .01}, 10 ^ 3];

选择几个切片时间：

Wolfram Language code: times = Range[0, 1, .1];
Wolfram Language code: qd = Map[{#, QnDispersion[data["SliceData", #]]}&, times];

绘制这些路径上的 分散度：

Wolfram Language code: Show[ListPlot[data], ListLinePlot[qd, PlotStyle -> Red]]

求一个班的孩子们的身高的 分散度：

Wolfram Language code: heights = Quantity[{134, 143, 131, 140, 145, 136, 131, 136, 143, 136, 133, 145, 147, 150, 150, 146, 137, 143, 132, 142, 145, 136, 144, 135, 141}, "Centimeters"];
Wolfram Language code: ListPlot[heights, Filling -> Axis, AxesLabel -> Automatic]
Wolfram Language code: qd = QnDispersion[heights]

绘制从中位数出发的 分散度：

Wolfram Language code: md = Median[heights]; n = Length[heights];
Wolfram Language code: ListPlot[{heights, {{0, md}, {n, md}}, {{0, md - qd}, {n, md - qd}}, {{0, m + qd}, {n, m + qd}}}, Filling -> {1 -> 0, 3 -> {4}}, Joined -> {False, True, True, True}, PlotStyle -> {Automatic, Automatic, Gray, Gray}, PlotLegends -> {"heights", "median", "Qn-bands"}, AxesLabel -> Automatic]

考虑来自标准正态分布的一组数据，其异常值由另一个展布较大的正态分布模拟：

Wolfram Language code: BlockRandom[ SeedRandom[10]; data = RandomVariate[MixtureDistribution[{0.95, 0.05}, {NormalDistribution[], NormalDistribution[0, 10]}], 10 ^ 4]; ]

用标准正态分布检验数据：

Wolfram Language code: DistributionFitTest[data, NormalDistribution[], "TestConclusion"]

计算 分散度：

Wolfram Language code: qd = QnDispersion[data]

选取距样本中位数三倍 分散度范围内的数据点，从而移除异常点：

Wolfram Language code: med = Median[data];
Wolfram Language code: ndata = Pick[data, Sign[Abs[data - med] - 3 qd], -1];

用标准正态分布检验新数据：

Wolfram Language code: DistributionFitTest[ndata, NormalDistribution[], "TestConclusion"]

从学生 分布中产生数据：

Wolfram Language code: data = RandomVariate[StudentTDistribution[1, 2, 1], 10 ^ 4];
Wolfram Language code: Histogram[data, {0.5}]

用三种度量计算数据的分散度：标准方差、截断方差的平方根和 分散度：

Wolfram Language code: ests = {StandardDeviation, Sqrt[TrimmedVariance[#]]&, QnDispersion};
Wolfram Language code: {sd, tsd, qn} = Through[ests[data]]

用自助法评估这三种分散度估计量的准确性：

Wolfram Language code: res = Table[Through[ests[RandomChoice[data, Length[data]]]], {10 ^ 3}];

估计量给出所给数据的最小的展布：

Wolfram Language code: StandardDeviation[res]

属性和关系  (2)

QnDispersion 是基于排序结果的估计量，其统计基于数据对间的绝对差值：

Wolfram Language code: data = RandomReal[1, 100]; diffs = Flatten[Outer[Subtract, data, data]];

选取差值中的正值，用 RankedMin 计算排序统计量：

Wolfram Language code: diffs = Pick[diffs, Sign[diffs], 1]; RankedMin[diffs, Binomial[Quotient[100, 2] + 1, 2]]

与缩放因子为 1 的 QnDispersion 相比较：

Wolfram Language code: qn = QnDispersion[data, 1]

数据对间差值的 Histogram，其中的红线表示 统计量的值：

Wolfram Language code: Histogram[diffs, {0.05}, Epilog -> {Red, Thick, Line[{{qn, 0}, {qn, 480}}], Red, Text["Qn", {qn, 510}]}, PlotRange -> {0, 550}]

QnDispersion、SnDispersion 和 StandardDeviation 是 NormalDistribution 的尺度参数的估计量：

Wolfram Language code: data = RandomVariate[NormalDistribution[1, 2], 10 ^ 4]; est = {QnDispersion, SnDispersion, StandardDeviation};
Wolfram Language code: TableForm[Through[est[data]], TableHeadings -> {est}]

用自助法评估估计量的准确性：

Wolfram Language code: {qnerror, snerror, stderror} = Variance[Table[Through[est[RandomChoice[data, 10 ^ 4]]], {10 ^ 3}]];

用估计结果计算关于 StandardDeviation 的相对效率：

Wolfram Language code: {stderror / qnerror, stderror / snerror}
Wolfram Research (2017)，QnDispersion，Wolfram 语言函数，https://reference.wolfram.com/language/ref/QnDispersion.html （更新于 2024 年）.

文本

Wolfram Research (2017)，QnDispersion，Wolfram 语言函数，https://reference.wolfram.com/language/ref/QnDispersion.html （更新于 2024 年）.

CMS

Wolfram 语言. 2017. "QnDispersion." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2024. https://reference.wolfram.com/language/ref/QnDispersion.html.

APA

Wolfram 语言. (2017). QnDispersion. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/QnDispersion.html 年

BibTeX

@misc{reference.wolfram_2026_qndispersion, author="Wolfram Research", title="{QnDispersion}", year="2024", howpublished="\url{https://reference.wolfram.com/language/ref/QnDispersion.html}", note=[Accessed: 05-November-2026]}

BibLaTeX

@online{reference.wolfram_2026_qndispersion, organization={Wolfram Research}, title={QnDispersion}, year={2024}, url={https://reference.wolfram.com/language/ref/QnDispersion.html}, note=[Accessed: 05-November-2026]}