QuartileDeviation
QuartileDeviation[data]
求出 data 中元素的四分位数偏差或者半四分位距.
QuartileDeviation[data,{{a,b},{c,d}}]
使用参数 a、b、c、d 指定的分位数定义.
QuartileDeviation[dist]
求出 dist 列表中四分位数偏差或者半内四分位范围的偏差.
更多信息




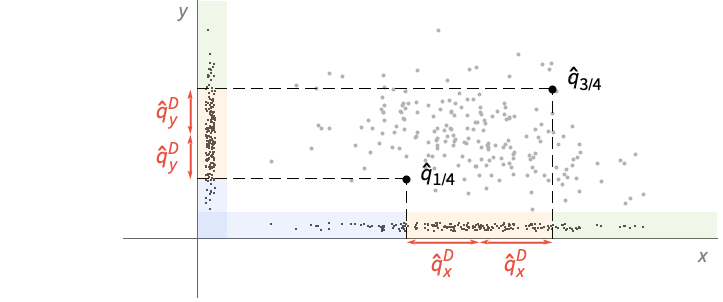
- QuartileDeviation 是散度的稳健度量,这意味着它对异常值不是很敏感.
- QuartileDeviation[data]
 is given by
is given by 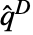 , where
, where  is given by Quartiles[data]. »
is given by Quartiles[data]. » - 对于 MatrixQ data,针对每个列向量计算四分位数偏差,QuartileDeviation[{{x1,y1,…},{x2,y2,…},…}] 等价于 {QuartileDeviation[{x1,x2,…}],QuartileDeviation[{y1,y2,…}]}. »
- 对于 ArrayQ data,四分位数偏差等价于 ArrayReduce[QuartileDeviation,data,1]. »
- QuartileDeviation[data,{{a,b},{c,d}}] 使用通过 Quartiles[data, {{a,b},{c,d}}] 计算所得的
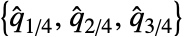 . »
. » - 参数 {{a,b},{c,d}} 的常见选择包括:
-
{{0,0},{1,0}} 逆经验 CDF {{0,0},{0,1}} 线性插值(California 法) {{1/2,0},{0,0}} 编号最接近 p n 的元素 {{1/2,0},{0,1}} 线性插值(水文学法;默认) {{0,1},{0,1}} 基于均值的估计(Weibull 法) {{1,-1},{0,1}} 基于众数的估计 {{1/3,1/3},{0,1}} 基于中位数的估计 {{3/8,1/4},{0,1}} 正态分布估计 - 参数的默认选择是 {{1/2,0},{0,1}}. »
- data 可以有以下其他形式和解释:
-
Association 数值(键被忽略) » SparseArray 数组,相当于 Normal[data] » QuantityArray 量组成的数组 » WeightedData 基于 EmpiricalDistribution » EventData 基于 SurvivalDistribution » TimeSeries, TemporalData, … 向量或数值组成的数组(忽略时间戳) » Image,Image3D RGB 通道的值或灰度的强度值 » Audio 所有通道的幅值 » DateObject, TimeObject 日期列表或时间列表 » - QuartileDeviation[dist] 由 InterquartileRange[dist]/2 给出. »
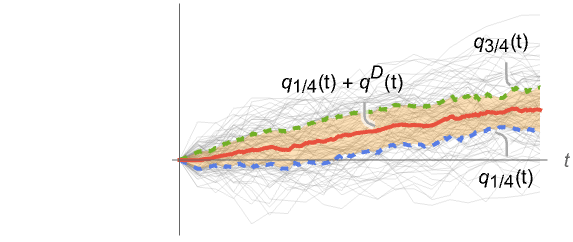
- 对于随机过程 proc,可计算时间 t 处切片分布 SliceDistribution[proc,t] 的四分位数偏差函数,即
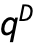 [t]=QuartileDeviation[SliceDistribution[proc,t]]. »
[t]=QuartileDeviation[SliceDistribution[proc,t]]. »


范例
打开所有单元关闭所有单元范围 (23)
基本用法 (8)
数组数据 (5)
矩阵的 QuartileDeviation 给出列的四分位数偏差:
当输入为 Association 时,QuartileDeviation 只作用于值:
可以像使用密集数组一样使用 SparseArray 数据:
求 QuantityArray 的四分位数偏差:
日期和时间 (5)
应用 (4)
基于 Mean 的量受到极值的严重影响:
计算随机过程路径集合切片的 QuartileDeviation:
属性和关系 (3)
QuartileDeviation 是线性插值 Quantile 函数值的一半:
InterquartileRange 求出的值是 QuartileDeviation 的两倍:
QuartileDeviation 是第一和第三个四分位数的一半:
可能存在的问题 (2)
QuartileDeviation 要求 data 都是数字:
QuartileDeviation 不是中位数与第一或第三分位数之间的差:
InterquartileRange 给出第一与第三分位数之间的差:
巧妙范例 (1)
取 20、100 和 300 个样本时 QuartileDeviation 估计值的分布:
文本
Wolfram Research (2007),QuartileDeviation,Wolfram 语言函数,https://reference.wolfram.com/language/ref/QuartileDeviation.html (更新于 2024 年).
CMS
Wolfram 语言. 2007. "QuartileDeviation." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2024. https://reference.wolfram.com/language/ref/QuartileDeviation.html.
APA
Wolfram 语言. (2007). QuartileDeviation. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/QuartileDeviation.html 年