RecurrenceTable[eqns,expr,{n,nmax}]
以求解递归方程 eqns 为基础,产生一组关于连续 n 的 expr 的值的列表.
RecurrenceTable[eqns,expr,nspec]
在 nspec 指定的 n 值范围上,产生一组 expr 的值.
RecurrenceTable[eqns,expr,{n1,…},{n2,…},…]
为连续的 n1,n2,… 产生 expr 的数组值.


RecurrenceTable
RecurrenceTable[eqns,expr,{n,nmax}]
以求解递归方程 eqns 为基础,产生一组关于连续 n 的 expr 的值的列表.
RecurrenceTable[eqns,expr,nspec]
在 nspec 指定的 n 值范围上,产生一组 expr 的值.
RecurrenceTable[eqns,expr,{n1,…},{n2,…},…]
为连续的 n1,n2,… 产生 expr 的数组值.
更多信息和选项

- eqns 必须是递归方程,它的解可以通过给出的初始条件或边界值确定.
- eqns 可以涉及形式 a[n+i] 的对象,其中 i 是任意固定整数.
- 范围 nspec 可以使用 Table 中的任何形式.
- 可以给出下列选项:
-
DependentVariables Automatic 所有独立变量的列表 Method Automatic 使用的方法 WorkingPrecision Automatic 内部计算使用的精度 - 在 DependentVariables->Automatic 下,RecurrenceTable 确定解析给出方程的独立变量.
- 在 WorkingPrecision->Automatic 下,精确计算有精确输入的结果,并且对于不精确的输入,精度根据每次迭代相确定.
- 在 WorkingPrecision->p 下,一个固定精度 p 用于所有迭代中.
- RecurrenceTable[u[t]sys,resp,{t,tmin,tmax}] 可用于解离散时间模型,其中 sys 可以是 TransferFunctionModel 或 StateSpaceModel,响应函数 resp 可为以下形式: »
-
"StateResponse" sys 对输入 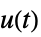 的状态响应
的状态响应"OutputResponse" sys 对输入 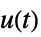 的输出响应
的输出响应
范例
打开所有单元 关闭所有单元范围 (12)
普通微分方程 (6)
差分-代数方程 (1)
与 RSolve 给出的符号解比较:
选项 (3)
DependentVariables (1)
WorkingPrecision (1)
对于更快速迭代,用 WorkingPrecision->MachinePrecision:
对于较慢速迭代,用 WorkingPrecision->p,但迭代的精度更高:
应用 (6)
属性和关系 (3)
RSolve 对于这个递归方程,求出一个符号解:
RecurrenceTable 对于相同问题,产生一个过程解:
使用 RecurrenceFilter 对信号滤波:
使用 RecurrenceTable 获得相同结果:
用 RFixedPoints 求非线性递归方程的不动点:
用 RStabilityConditions 分析不动点的稳定性:
用 RecurrenceTable 解方程:
相关链接
文本
Wolfram Research (2008),RecurrenceTable,Wolfram 语言函数,https://reference.wolfram.com/language/ref/RecurrenceTable.html (更新于 2024 年).
CMS
Wolfram 语言. 2008. "RecurrenceTable." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2024. https://reference.wolfram.com/language/ref/RecurrenceTable.html.
APA
Wolfram 语言. (2008). RecurrenceTable. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/RecurrenceTable.html 年
BibTeX
@misc{reference.wolfram_2025_recurrencetable, author="Wolfram Research", title="{RecurrenceTable}", year="2024", howpublished="\url{https://reference.wolfram.com/language/ref/RecurrenceTable.html}", note=[Accessed: 16-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_recurrencetable, organization={Wolfram Research}, title={RecurrenceTable}, year={2024}, url={https://reference.wolfram.com/language/ref/RecurrenceTable.html}, note=[Accessed: 16-February-2026]}