RegionFit

RegionFit[{p1,p2,…},"model"]

点 p1,p2,…に最もフィットする幾何学的領域"model"を求める．

RegionFit[{p1,p2,…},"model","prop"]

どのフィット特性"prop"を返すかを指定する．

詳細とオプション

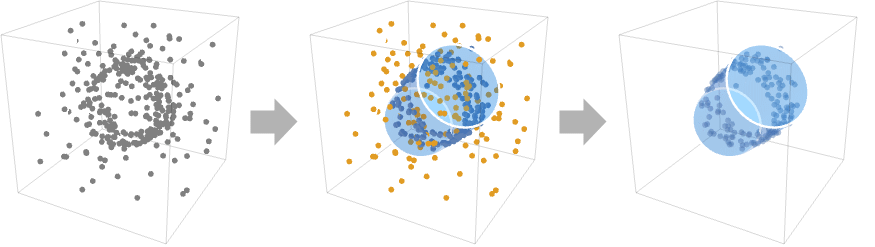
  • RegionFitは，サンプルコンセンサスモデルとしても知られている．
  • RegionFitは，通常，点の集合をフィットして領域を再構築するために使われる．
  • RegionFit[{p1,p2,…},"model"]は，指定された"model"のパラメータを点の集合から反復的に推定することで，最も多くの点 piを含む領域を求める．
  • 次は，使用可能な2Dの"model"指定である．
  • "Line"無限の線
    "Circle"円
  • 次は，使用可能な3Dの"model"指定である．
  • "Line"無限の線
    "Circle"円
    "Plane"平面
    "Sphere"球
    "Cylinder"円柱
    "Cone"円錐
  • RegionFit[Point[{p1,p2,…}]]は，事実上，RegionFit[{p1,p2,…}]に等しい．
  • 点 piの頂点法線 niはPoint[{p1,p2,…},VertexNormals{n1,n2,…}]で指定できる．
  • RegionFit[{p1,p2,…},"model","prop"]はフィット特性"prop"の値を返す．
  • 次は，使用可能なフィット特性"prop"である．
  • "BestFit"最良のモデル候補
    "Points"点集合
    "Inliers"モデル候補にフィットする点
    "Outliers"モデル候補にフィットしない点
    "DistanceVariance"モデル候補までの距離の分散
    "Distances"最良のモデル候補までの距離
    {prop1,prop2,…}いくつかのフィット特性
  • 次は使用可能なオプションである．
  • ConfidenceLevelAutomatic外れ値がないサンプルの望ましい確率
    MethodAutomatic使用するメソッド
    PerformanceGoal$PerformanceGoal最適化しようとするパフォーマンスの局面
    Tolerance Automatic使用する数値による許容範囲
    VertexNormalsNone点の頂点法線
    WorkingPrecision Automatic計算精度
  • 次は，Methodの可能な設定である．
  • "RANSAC"ランダムサンプルコンセンサス
    "LMEDS"正方形の最小中央値
    "MSAC"M推定器サンプルコンセンサス
    "RRANSAC"ランダム化されたRANSAC
    "RMSAC"ランダム化されたMSAC
    "MLESAC"最尤推定サンプルコンセンサス
    "PROSAC"前進ランダムコンセンサス

例題

すべて開くすべて閉じる

例  (2)

点集合にフィットする円を求める：

フィットを示す：

円柱にフィットする多くの外れ値がある点集合：

データを使ってフィットする領域を可視化する：

データから最もよくフィットする円柱までの距離の分布：

スコープ  (13)

データ  (4)

RegionFitは座標に使うことができる：

点のリスト：

点の集合：

点の配向集合：

モデル  (7)

点の集合に最もフィットするInfiniteLineを得る：

Circle：

3DのInfiniteLine：

Hyperplane：

Sphere：

Cylinder：

Cone：

特性  (2)

RegionFitは最もフィットする領域を与える：

最もよくフィットする領域から各点までの距離：

距離の分散：

インライヤーと外れ値：

オプション  (4)

Tolerance  (1)

Toleranceを使ってインライヤーの最大距離を制御する：

WorkingPrecision  (3)

機械演算で最良フィットモデルを計算する：

厳密値を使ってフィットを求める：

30桁精度でフィットを求める：

アプリケーション  (3)

円周上の点集合についてパラメータ化された最適フィット領域を求める：

厳密なフィッを示す：

ノイズがある点の集合：

パラメータ化された最適フィット領域を求める：

データでフィットされた領域を可視化する：

点の集合を通る線の方程式を求める：

特性と関係  (1)

RegionFitとFitは，ほぼ完全な線形データについてLeastSquaresを使って同等のフィットを生成する：

Fitを使って線の方程式を求める：

RegionFitを使って線の領域を求める：

結果を比較する：

Fitはすべての点について最小二乗誤差を最小化するのに対し，RegionFitは外れ値を無視する：

外れ値があるデータを求める：

新たなフィットを示す：

Wolfram Research (2021), RegionFit, Wolfram言語関数， https://reference.wolfram.com/language/ref/RegionFit.html.

テキスト

Wolfram Research (2021), RegionFit, Wolfram言語関数， https://reference.wolfram.com/language/ref/RegionFit.html.

CMS

Wolfram Language. 2021. "RegionFit." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/RegionFit.html.

APA

Wolfram Language. (2021). RegionFit. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/RegionFit.html

BibTeX

@misc{reference.wolfram_2024_regionfit, author="Wolfram Research", title="{RegionFit}", year="2021", howpublished="\url{https://reference.wolfram.com/language/ref/RegionFit.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_regionfit, organization={Wolfram Research}, title={RegionFit}, year={2021}, url={https://reference.wolfram.com/language/ref/RegionFit.html}, note=[Accessed: 21-November-2024 ]}