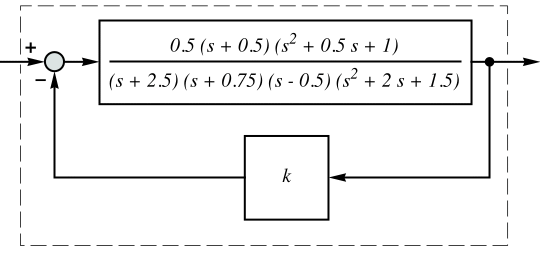
RootLocusPlot
RootLocusPlot[lsys,{k,kmin,kmax}]
生成线性时不变系统 lsys 的根轨迹图,其中参数 k 的范围从 kmin 到 kmax 变化.
更多信息和选项



- RootLocusPlot 对范围为 k 值下的闭环系统绘制极点的位置.
- RootLocusPlot 将参数 k 视为局部变量,事实上使用 Block.
- 系统模型 lsys 可以是 StateSpaceModel 或者 TransferFunctionModel.
- RootLocusPlot 有与 Graphics 相同的选项,但有如下附加内容和变动: [所有选项的列表]
-
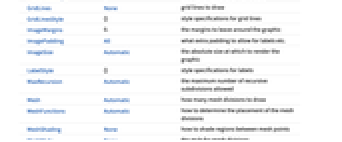
Axes True 是否画出坐标轴 ColorFunction Automatic 如何对轨迹配色 ColorFunctionScaling True 是否对 ColorFunction 的参变量进行缩放 EvaluationMonitor None 要在每一个参数求值的地方求值的表达式 Exclusions Automatic 要排除的参数值 ExclusionsStyle None 在被排除点处要绘制的内容 FeedbackType "Negative" 反馈类型 MaxRecursion Automatic 所允许的最大第归细分次数 Mesh Automatic 绘制多少个网格分割 MeshFunctions Automatic 如何确定网格分割的布局 MeshShading None 如何在网格点间的区域添加阴影 MeshStyle None 网格分割样式 Method Automatic 确定轨迹的方法 PerformanceGoal $PerformanceGoal 想要优化的性能特征 PlotPoints Automatic 采样参数点的初始数目 PlotRange Automatic 要包含的值的范围 PlotRangeClipping True 是否在制图范围内裁剪 PlotStyle Automatic 指定轨迹式样的图形指令 PlotTheme $PlotTheme 图形的全局主题 PoleZeroMarkers Automatic 极点和零点的标符 RegionFunction (True&) 如何确定是否包括点 PlotLegends None 根轨迹的图例 WorkingPrecision MachinePrecision 内部计算所用的精度 - RootLocusPlot 采用一个 Method 选项来指定计算根轨迹所用的方法.
- 在 Method->"GenericSolve" 设置下,轨迹是通过计算采样点处的根,再对它们进行排序来确定的.
- 在 Method->"NDSolve" 设置下,RootLocusPlot 使用 NDSolve 来求解微分方程
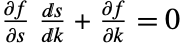 ,其中
,其中  是闭环系统的特征方程,
是闭环系统的特征方程,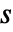 是复变量.
是复变量. - Method->{"NDSolve",opt1->val1,opt2->val2,…} 使用特定的 NDSolve 选项.
- 对特定的 k 值,闭环极点可以通过 Mesh、MeshFunctions 和 MeshStyle 的适当设置来绘制.
- 开环极点和零点,以及闭环极点的标符可以通过设置 PoleZeroMarkers 选项来指定.
- RegionFunction 的参变量是 x、y 和 k.
所有选项的列表


范例
打开所有单元关闭所有单元
Wolfram Research (2010),RootLocusPlot,Wolfram 语言函数,https://reference.wolfram.com/language/ref/RootLocusPlot.html (更新于 2014 年).
文本
Wolfram Research (2010),RootLocusPlot,Wolfram 语言函数,https://reference.wolfram.com/language/ref/RootLocusPlot.html (更新于 2014 年).
CMS
Wolfram 语言. 2010. "RootLocusPlot." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2014. https://reference.wolfram.com/language/ref/RootLocusPlot.html.
APA
Wolfram 语言. (2010). RootLocusPlot. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/RootLocusPlot.html 年