RotationMatrix
给出二维旋转矩阵,使二维向量逆时针旋转 θ 角度.
RotationMatrix[θ,w]
给出三维旋转矩阵,根据三维向量 w 逆时针旋转.
RotationMatrix[{u,v}]
给出旋转矩阵,在全维中,旋转向量 u 到向量 v 的方向.
RotationMatrix[θ,{u,v}]
给出旋转矩阵,旋转在 u 和 v 的确定的平面 θ 角.
更多信息和选项

- RotationMatrix 给出绕原点旋转的向量的矩阵.
- 通常使用两种不同的矩阵旋转方式.
- RotationMatrix 的设置符合向量的规定,给出矩阵 m,其中 m.r 生成向量 r 的旋转矩阵.
- Transpose[RotationMatrix[…]] 根据可选的坐标系统规定,生成旋转矩阵,其中 r.m 生成向量 r 的旋转矩阵.
- 在 RotationMatrix 中的角度为弧度, θ Degree 或 θ° 是用度数表示的角度.
- 在 RotationMatrix[θ,{u,v}] 中,正 θ 角表示向量 u 到向量 v 的夹角.
- RotationMatrix[θ] 等同于 RotationMatrix[θ,{{1,0},{0,1}}].
- RotationMatrix[θ,w] 等同于 RotationMatrix[θ,{u,v}],其中 u⊥w, v⊥w 和 u,v,w 构成右手系坐标系统.
- RotationMatrix 给出一个行列式为 1 的正交矩阵,
 维可以认为是组
维可以认为是组 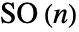 的一个元素.
的一个元素. - RotationMatrix 支持选项 TargetStructure,该选项指定了返回的矩阵的结构. TargetStructure 的可能的设置包括:
-
Automatic 自动选择返回的形式 "Dense" 用稠密矩阵表示结果 "Orthogonal" 用正交矩阵表示结果 "Unitary" 用酉矩阵表示结果 - RotationMatrix[…,TargetStructureAutomatic] 等价于 RotationMatrix[…,TargetStructure"Dense"].
范例
打开所有单元关闭所有单元范围 (6)
属性和关系 (9)
RotationMatrix[θ,{u,v}] 的逆是由 RotationMatrix[-θ,{u,v}] 给出:
RotationMatrix[θ,{u,v}] 的逆也是由 RotationMatrix[θ,{v,u}] 给出:
在二维图形中, RotationMatrix[θ] 的旋转由 RotationMatrix[-θ] 给出:
在三维图形中, RotationMatrix[θ,w] 的旋转由 RotationMatrix[θ,-w] 给出:
文本
Wolfram Research (2007),RotationMatrix,Wolfram 语言函数,https://reference.wolfram.com/language/ref/RotationMatrix.html (更新于 2024 年).
CMS
Wolfram 语言. 2007. "RotationMatrix." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2024. https://reference.wolfram.com/language/ref/RotationMatrix.html.
APA
Wolfram 语言. (2007). RotationMatrix. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/RotationMatrix.html 年