RotationTransform
gives a TransformationFunction that represents a rotation in 2D by θ radians about the origin.
RotationTransform[θ,p]
gives a 2D rotation about the 2D point p.
RotationTransform[θ,w]
gives a 3D rotation around the direction of the 3D vector w.
RotationTransform[θ,w,p]
gives a 3D rotation around the axis w anchored at the point p.
RotationTransform[{u,v}]
gives a rotation about the origin that transforms the vector u to the direction of the vector v.
RotationTransform[{u,v},p]
gives a rotation about the point p that transforms u to the direction of v.
RotationTransform[θ,{u,v},…]
gives a rotation by θ radians in the plane spanned by u and v.
Details

- RotationTransform gives a TransformationFunction that can be applied to vectors.
- θ Degree or θ° specifies an angle in degrees.
- RotationTransform[θ,{u,v},p] can be used to specify any rotation about any point p, in any number of dimensions.
- Positive θ in RotationTransform[θ,{u,v},p] corresponds to going from the direction of u toward the direction of v.
- RotationTransform[θ] is equivalent to RotationTransform[θ,{{1,0},{0,1}}].
- RotationTransform[θ,w] is equivalent to RotationTransform[θ,{u,v}], where u⊥w, v⊥w, and u,v,w form a right-handed coordinate system.
- RotationTransform[θ,{u,v}] can effectively specify any element of the
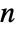 -dimensional rotation group
-dimensional rotation group 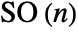 . RotationTransform[θ,{u,v},p] can effectively specify any element of the
. RotationTransform[θ,{u,v},p] can effectively specify any element of the 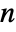 -dimensional special Euclidean group.
-dimensional special Euclidean group.
Examples
open allclose allBasic Examples (4)
Scope (9)
Rotation by θ radians about the point {px,py}:
Rotation by θ radians around the ![]() axis about the point {px,py,pz}:
axis about the point {px,py,pz}:
A 2D rotation by θ in the ![]() plane:
plane:
A 3D rotation by θ in the ![]() plane:
plane:
A 4D rotation by θ in the ![]() plane:
plane:
A 3D rotation by θ in the plane parametrized by s{1,-1,1}+t{1,1,1}:
This rotates the vector {1,1,1}:
Generate the transform for a symbolic vector, assuming that all quantities are real:
Simplify the result further by assuming that {x,y,z} is a unit vector:
Applications (5)
Basic (2)
Parametrize a great circle passing through the points u and v on a sphere:
The great circle passing through {1,-1,1}/√3 and {1,1,1}/√3 :
This shows the great circle and points on the unit sphere:
Using GeometricTransformation:
Image Transformations (3)
Rotate an image about its {0,0} origin using RotationTransform:
Rotate about the image center:
Specify a different center of rotation in the standard image coordinate system:
Properties & Relations (9)
The rotation transformation is an isometric transform, i.e. preserves distances:
The linear part of a rotation transform is given by RotationMatrix:
The matrix for the linear part is OrthogonalMatrixQ for real rotations:
The inverse of RotationTransform[θ,{u,v}] is RotationTransform[-θ,{u,v}]:
The inverse of RotationTransform[θ,{u,v}] is RotationTransform[θ,{v,u}]:
If u or v is not real, the relationship is more complex:
The inverse of RotationTransform[θ] is given by RotationTransform[-θ]:
The inverse of RotationTransform[θ,w] is given by RotationTransform[-θ,w]:
The inverse of RotationTransform[θ,w] is also given by RotationTransform[θ,-w]:
If w is not real, the relationship is more complex:
The composition of rotations is a rotation:
For graphics transformation, use Rotate:
Possible Issues (1)
Text
Wolfram Research (2007), RotationTransform, Wolfram Language function, https://reference.wolfram.com/language/ref/RotationTransform.html.
CMS
Wolfram Language. 2007. "RotationTransform." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/RotationTransform.html.
APA
Wolfram Language. (2007). RotationTransform. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/RotationTransform.html