RotationTransform
2Dにおける原点を中心とした θ ラジアンの回転を表すTransformationFunctionを返す.
RotationTransform[θ,p]
2Dの点 p を中心とした2D回転を与える.
RotationTransform[θ,w]
3Dベクトル w の方向周囲での3D回転を与える.
RotationTransform[θ,w,p]
点 p に固定された軸 w の周りでの3D回転を与える.
RotationTransform[{u,v}]
ベクトル u をベクトル v の方向に変換する原点を中心とした回転を与える.
RotationTransform[{u,v},p]
点 p を中心とした u を v の方向に変換する回転を与える.
RotationTransform[θ,{u,v},…]
u と v でスパンされた平面における θ ラジアンの回転を与える.
詳細

- RotationTransformは,ベクトルに適用できるTransformationFunctionを与える.
- θ Degreeすなわち θ°は角を度で指定する.
- RotationTransform[θ,{u,v},p]は,任意の次元における任意の点 p を中心とした任意の回転を指定するのに使うことができる.
- RotationTransform[θ,{u,v},p]における正の θ は方角 u から方角 v へ進むことに相当する.
- RotationTransform[θ]はRotationTransform[θ,{{1,0},{0,1}}]に等しい.
- RotationTransform[θ,w]はRotationTransform[θ,{u,v}]に等しい.ただし,u⊥w,v⊥w,u,v,w で右手座標系を形作る.
- RotationTransform[θ,{u,v}]は,実質的に
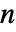 次元の回転群
次元の回転群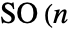 )の任意の要素を指定することができる.RotationTransform[θ,{u,v},p]は,実質的に,
)の任意の要素を指定することができる.RotationTransform[θ,{u,v},p]は,実質的に,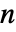 次元の特別な運動群の任意の要素を指定することができる.
次元の特別な運動群の任意の要素を指定することができる.
例題
すべて開くすべて閉じるスコープ (9)
アプリケーション (5)
画像変換 (3)
RotationTransformを使って原点{0,0}の周りで画像を回転させる:
特性と関係 (9)
回転変換の線形部分はRotationMatrixで与えられる:
線形部分の行列は,実際の回転についてのOrthogonalMatrixQである:
RotationTransform[θ,{u,v}]の逆関数はRotationTransform[-θ,{u,v}]である:
RotationTransform[θ,{u,v}]の逆関数はRotationTransform[θ,{v,u}]である:
RotationTransform[θ]の逆関数はRotationTransform[-θ]で与えられる:
RotationTransform[θ,w]の逆関数はRotationTransform[-θ,w]で与えられる:
RotationTransform[θ,w]の逆関数もまたRotationTransform[θ,-w]で与えられる:
グラフィックスの変換にはRotateを使う:
テキスト
Wolfram Research (2007), RotationTransform, Wolfram言語関数, https://reference.wolfram.com/language/ref/RotationTransform.html.
CMS
Wolfram Language. 2007. "RotationTransform." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/RotationTransform.html.
APA
Wolfram Language. (2007). RotationTransform. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/RotationTransform.html