RulePlot

RulePlot[sys]

generates a plot representing the rule for the computational system sys.

RulePlot[sys,init,t]

generates a plot of the evolution of the system sys from initial condition init for t steps.

RulePlot[sys,evol]

generates a plot of the evolution evol assuming it is derived from a system of the form sys.

Details and Options

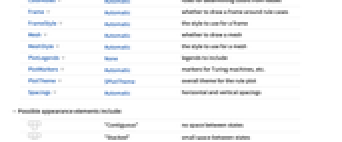
  • Possible computational systems sys include:
  • CellularAutomaton[spec]cellular automaton
    TuringMachine[spec]Turing machine
    SubstitutionSystem[spec]substitution system
    BooleanFunction[spec]Boolean function
  • TuringMachine[{rule,s,k}] can be used to specify a Turing machine in which rule does not uniquely specify a transformation for each of the s k possible configurations, but that nevertheless will be rendered assuming s head states and k tape colors.
  • RulePlot works with 1D and 2D systems.
  • Options include:
  • Appearance Automaticoverall appearance
    ColorRules Automaticrules for determining colors from values
    Frame Automaticwhether to draw a frame around rule cases
    FrameStyle Automaticthe style to use for a frame
    Mesh Automaticwhether to draw a mesh
    MeshStyle Automaticthe style to use for a mesh
    PlotLegends Nonelegends to include
    PlotMarkers Automaticmarkers for Turing machines, etc.
    PlotTheme $PlotThemeoverall theme for the rule plot
    Spacings Automatichorizontal and vertical spacings
  • Possible appearance elements include:
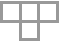
  • "Contiguous"no space between states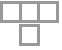
    "Stacked"small space between states
    "Arrow"draw an arrow between states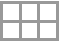
    "Squares"squares for cells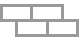
    "Bricks"bricks for cells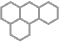
    "Hexagons"hexagons for cells
    "Simplified"simplified rule cases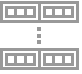
    "Short"show shortened list of rules
  • Possible plot legend forms include:
  • "Icon"use an icon as the legend
    "Text"use text as the legend
    exprarbitrary plot legend
  • In the form RulePlot[sys,evol], specific rules are typically ignored; only the implicit or explicit specification of number of colors, states, etc. is used.

Examples

open allclose all

Basic Examples  (5)

Return the rule icon for elementary cellular automaton rule 30:

Plot the evolution of a cellular automaton for 10 steps:

Include the rule icon:

Plot the evolution of a Turing machine:

Return its rule icon:

Generate the evolution of a Turing machine:

Use RulePlot to display the history, using information on the rule to determine the form:

Show the rule icon for a substitution system:

Scope  (42)

System Rules  (31)

CellularAutomaton  (11)

Elementary cellular automaton rule 90:

Cellular automaton with more than two colors:

Cellular automaton with range greater than 1:

Cellular automaton with fractional range:

Totalistic 3-color cellular automaton:

Outer totalistic 3-color cellular automaton:

General two-dimensional cellular automaton:

Totalistic two-dimensional 5-neighbor rule:

Totalistic two-dimensional 9-neighbor rule:

Outer totalistic two-dimensional rule:

Rules specified using associations:

TuringMachine  (8)

Turing machine rule 2506:

Turing machine with more than two states:

Turing machine with more than two colors:

Turing machines specified by rules:

Explicitly specify values of the number of states s and the number of colors k for the same transition rules:

Single-state Turing machine heads are represented with a dot:

Increase the number of states to change the representation:

An underspecified Turing machine does not have rules for all s k input configurations:

A nondeterministic Turing machine specifies different rules for the same input configuration:

SubstitutionSystem  (8)

String substitution system for two characters:

String substitution system for more than two characters:

String substitution system for length-2 strings:

String substitution system for strings of different lengths:

List substitution system for two integer values:

List substitution system for more than two integer values:

List substitution system with lists of different lengths:

Two-dimensional substitution systems:

BooleanFunction  (4)

Boolean function in two variables:

Boolean function in more than two variables:

Boolean function based on a vector of truth values:

Boolean function based on a table of truth rules:

System Evolution  (11)

CellularAutomaton  (5)

Evolution of rule 30 for 10 steps:

Evolution for 50 steps from a single 1 on a background of 0s:

Evolution of a 3-color cellular automaton:

Evolution from a single 1 on a background of repeated 0110 blocks:

Evolution of a 3-color totalistic code:

Evolution of a 3-color outer totalistic code:

Evolution of rules specified by associations:

TuringMachine  (6)

Evolution of a 2-state, 2-color Turing machine, starting with a tape of four 0s:

Evolution starting with an infinite tape of 0s:

Evolution of a 3-state, 2-color Turing machine:

Evolution starting with a tape of 1 on a background of 0s:

Evolution of a 2-state, 3-color Turing machine:

Evolution with the head initially in state 2:

Evolution of a Turing machine specified by rules, starting from a background of repeated 021 blocks:

A nondeterministic Turing machine can give different evolutions depending on the order of its rules:

An underspecified Turing machine does not have rules for all s k input configurations:

Specifying a complete set of rules eliminates the fixed point:

Options  (19)

Appearance  (4)

Use hexagons:

Use bricks:

Sometimes you can get a simplified result that shows cells whose value does not matter:

Shorten the display of the rule set:

ColorRules  (1)

Specify color rules for explicit values or patterns:

Frame  (1)

Do not use a frame:

FrameStyle  (2)

Make the frame blue:

Give a composite directive for the frame:

Mesh  (1)

By default, a mesh is drawn around individual cells:

Do not use a mesh:

MeshStyle  (2)

Make the mesh blue:

Give a composite directive for the mesh:

PlotLegends  (3)

Give a plot legend describing the rule in text:

Give a plot legend describing the rule as an icon:

Give an arbitrary plot legend:

PlotMarkers  (2)

Make the marker of a Turing machine gray:

Draw the outline of the default markers:

PlotTheme  (2)

Use the web plot theme:

Use this theme without a mesh:

Use the scientific plot theme:

Spacings  (1)

Change the spacing inside the frame:

Change the spacing on each side of the icon:

Applications  (2)

Use RulePlot to legend the evolution of a CellularAutomaton:

Properties & Relations  (2)

Plot the evolution of a cellular automaton with ArrayPlot:

Use RulePlot to plot the evolution and the rule icon:

Plot the evolution of a Turing machine with ArrayPlot:

Use RulePlot to plot the evolution and the head of the machine:

Wolfram Research (2016), RulePlot, Wolfram Language function, https://reference.wolfram.com/language/ref/RulePlot.html (updated 2021).

Text

Wolfram Research (2016), RulePlot, Wolfram Language function, https://reference.wolfram.com/language/ref/RulePlot.html (updated 2021).

CMS

Wolfram Language. 2016. "RulePlot." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2021. https://reference.wolfram.com/language/ref/RulePlot.html.

APA

Wolfram Language. (2016). RulePlot. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/RulePlot.html

BibTeX

@misc{reference.wolfram_2024_ruleplot, author="Wolfram Research", title="{RulePlot}", year="2021", howpublished="\url{https://reference.wolfram.com/language/ref/RulePlot.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_ruleplot, organization={Wolfram Research}, title={RulePlot}, year={2021}, url={https://reference.wolfram.com/language/ref/RulePlot.html}, note=[Accessed: 21-November-2024 ]}