SiegelTukeyTest
SiegelTukeyTest[{data1,data2}]
检验 data1 和 data2 的方差是否相等.
SiegelTukeyTest[dspec,![]() ]
]
检验 ![]() 的差量度量.
的差量度量.
SiegelTukeyTest[dspec,![]() ,"property"]
,"property"]
返回 "property" 值.
更多信息和选项


- SiegelTukeyTest 在 data1 和 data2 上执行一个假设检验,其中零假设
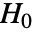 ,其总体方差比例为
,其总体方差比例为 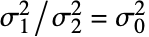 ;对立假设为
;对立假设为 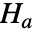
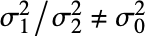 .
. - 默认情况下,返回一个概率值或
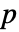 .
. 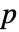 值越小,
值越小,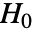 为真的可能性越低.
为真的可能性越低.- 变量
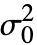 可以是任意正实数.
可以是任意正实数. - dspec 中的 data 必须是单变量 {x1,x2,…}.
- SiegelTukeyTest 假设 data 关于一个共同的中位数对称.
- SiegelTukeyTest[data,
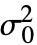 ,"HypothesisTestData"] 返回一个 HypothesisTestData 对象 htd,使用 htd["property"] 的形式可以用来提取额外检验结果和属性.
,"HypothesisTestData"] 返回一个 HypothesisTestData 对象 htd,使用 htd["property"] 的形式可以用来提取额外检验结果和属性. - SiegelTukeyTest[data,
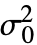 ,"property"] 可以用于直接给出 "property" 值.
,"property"] 可以用于直接给出 "property" 值. - 与检验结果的报告相关的属性包括:
-
"PValue" 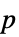 值组成的列表
值组成的列表"PValueTable" 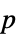 值组成的格式化表格
值组成的格式化表格"ShortTestConclusion" 检验结论的简短描述 "TestConclusion" 检验结论的描述 "TestData" 检验统计量和 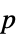 值对组成的列表
值对组成的列表"TestDataTable" 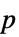 值和检验统计量组成的格式化表格
值和检验统计量组成的格式化表格"TestStatistic" 检验统计量组成的列表 "TestStatisticTable" 检验统计量组成的格式化表格 - 检验统计量针对合并样本
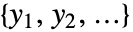 计算为
计算为 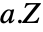 ,其中如果
,其中如果 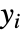 来自 data1 ,则
来自 data1 ,则 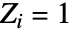 ,否则为零;
,否则为零;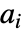 是与每个
是与每个 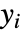 相关的秩次. 在
相关的秩次. 在 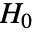 下,假设统计量服从NormalDistribution.
下,假设统计量服从NormalDistribution. - SiegelTukeyTest 比起 ConoverTest 是效能较低的基于秩次的检验方法,并且当 datai 不服从正态分布时,可以作为 FisherRatioTest 的一个替换.
- 可以使用以下选项:
-
AlternativeHypothesis "Unequal" 备择假定的不等性 SignificanceLevel 0.05 用于诊断和报告的分界点 VerifyTestAssumptions Automatic 设置要运行哪个诊断检验 - 对于 SiegelTukeyTest,选择一个临界值
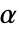 ,使得只有当
,使得只有当 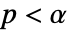 时,拒绝
时,拒绝 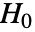 . 用于 "TestConclusion" 和 "ShortTestConclusion" 属性的
. 用于 "TestConclusion" 和 "ShortTestConclusion" 属性的 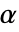 值由 SignificanceLevel 选项控制.
值由 SignificanceLevel 选项控制. 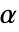 值也用于包括对称性检验的假设的诊断检验中. 默认情况下,
值也用于包括对称性检验的假设的诊断检验中. 默认情况下,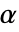 设为 0.05.
设为 0.05. - 在 SiegelTukeyTest 中,VerifyTestAssumptions 的已命名设置包括:
-
"Symmetry" 验证所有数据都是对称的
范例
打开所有单元关闭所有单元基本范例 (2)
范围 (7)
检验 (5)
创建一个 HypothesisTestData 对象,用以进行重复属性提取:
创建一个 HypothesisTestData 对象,用以重复属性提取:
从一个 HypothesisTestData 对象提取某些属性:
选项 (7)
AlternativeHypothesis (3)
SignificanceLevel (2)
属性和关系 (6)
在 ![]() 下,检验统计量服从一个 NormalDistribution[0,1]:
下,检验统计量服从一个 NormalDistribution[0,1]:
与 FisherRatioTest 不同,Siegel-Tukey 检验并不假定正态性成立:
FisherRatioTest 导致对 ![]() -值的低估:
-值的低估:
Siegel-Tukey 检验假设数据关于一个共同的中位数对称:
当数据不对称时,检验统计量的分布不服从 NormalDistribution[0,1]:
PearsonChiSquareTest 用于检验数据关于一个共同的中位数的对称性:
警告信息中的 ![]() 值与 PearsonChiSquareTest 中的值一致:
值与 PearsonChiSquareTest 中的值一致:
当输入为 TimeSeries 时,Siegel-Tukey 检验忽略时间戳:
Siegel–Tukey 检验识别出了一个恰好有两条路径的 TemporalData 的路径结构:
文本
Wolfram Research (2010),SiegelTukeyTest,Wolfram 语言函数,https://reference.wolfram.com/language/ref/SiegelTukeyTest.html.
CMS
Wolfram 语言. 2010. "SiegelTukeyTest." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/SiegelTukeyTest.html.
APA
Wolfram 语言. (2010). SiegelTukeyTest. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/SiegelTukeyTest.html 年