SignTest

SignTest[data]

检验 data 的中位数是否为0.

SignTest[{data1,data2}]

检验 data1– data2 的中位数是否为0.

SignTest[dspec,μ0]

对 μ0 检验一个位置量数.

SignTest[dspec,μ0,"property"]

返回 "property" 的值.

更多信息和选项

  • SignTest 检验零假设 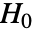与替代假设 ：
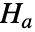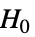
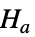
  • data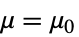
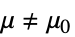
    {data1,data2}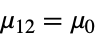
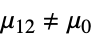
  • 其中 μ 是 data 的总体中位数，μ12是两个数据集 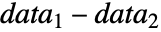的配对差中位数.
  • 默认情况下，返回一个概率值或者 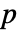值.
  • 一个小的 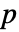值表明 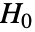不可能为真.
  • dspec 中的数据可以是单变量 {x1,x2,…} 或者多变量 {{x1,y1,…},{x2,y2,…},…}.
  • 如果给定两个样本，则它们必须具有相同的长度.
  • 变量 μ0 可以是一个实数，或者长度等于数据维度的一个实向量.
  • SignTest[dspec,μ0,"HypothesisTestData"] 返回一个 HypothesisTestData 对象 htd，可以使用 htd["property"] 的形式来提取额外检验结果和属性.
  • SignTest[dspec,μ0,"property"] 可以用于直接给出 "property" 值.
  • 与检验结果的报告相关的属性包括：
  • "DegreesOfFreedom"检验中所用的自由度
    "PValue" 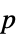值列表
    "PValueTable" 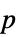值组成的格式化表格
    "ShortTestConclusion"检验结论的简短描述
    "TestConclusion"检验结论的描述
    "TestData"检验统计量和 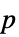值对的列表
    "TestDataTable" 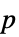值和检验统计量组成的格式化表格
    "TestStatistic"检验统计量组成的列表
    "TestStatisticTable"检验统计量组成的格式化表格
  • 对于单变量样本，SignTest 执行对成对样本的中位数的符号检验. 假设检验统计量服从BinomialDistribution[n,1/2]，其中 n 是 dspec 中不等于 μ0 的元素数目.
  • 对于多变量样本，SignTest 使用空间符号对成对样本执行一个仿射不变检验. 假设检验统计量服从一个 ChiSquareDistribution[dim]，其中 dim 是 dspec 的维度.
  • 可以使用以下选项：
  • AlternativeHypothesis "Unequal"备择假设的不等性
    MaxIterations Automatic多变量中位数检验的最大迭代
    Method Automatic用于 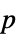-值的方法
    SignificanceLevel 0.05用于诊断和报告的分界点
  • 对于 SignTest，选择一个临界值 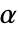，使得当且仅当 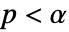时，否定 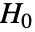. 用于 "TestConclusion" 和 "ShortTestConclusion" 属性的 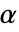值由 SignificanceLevel 选项控制. 默认情况下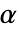， 设为 0.05.

范例

打开所有单元关闭所有单元

基本范例  (4)

检验一个总体的中位数是否为零：

检验多变量总体的空间中位数是否是某个固定的值：

计算检验统计量：

将成对数据的中位数差值与某个特定值比较：

在一个表格中报告检验结果：

创建一个 HypothesisTestData 对象，用以进行重复属性提取：

可用属性列表：

提取单个属性或者属性列表：

范围  (13)

检验  (10)

检验 与 ：

当中位数接近 μ0 时， 值通常较大：

当位置（location）远离 μ0 时， 值通常较小：

使用 Automatic 等价于检验中位数是否为0：

检验 与 ：

当中位数接近 μ0 时， 值通常较大：

当位置远离 μ0 时， 值通常较小：

检验多变量总体的中位数向量是否为零向量：

也可以对 {0.1,0,-0.05,0} 进行检验：

检验 与 ：

当位置不相等时， 值通常较小：

当位置相等时， 值通常较大：

检验 与 ：

数据集的顺序影响检验结果：

检验两个多变量总体的中位数差异向量是否为零向量：

或者，对 {1,0,-1,0} 进行检验：

创建一个 HypothesisTestData 对象，用以进行重复属性提取：

可用于提取的属性：

从 HypothesisTestData 对象中提取某些属性：

值和检验统计量：

同时提取任意数目的属性：

值和检验统计量：

报告  (3)

将检验结果制作成表格：

将检验表格提取项目，制作成定制的报告：

将 值或者检验统计量制作成表格：

来自表格的 值：

来自表格的检验统计量：

选项  (9)

AlternativeHypothesis  (3)

默认情况下，执行双侧检验：

检验 与 ：

执行双侧检验或者一个单侧检验：

检验 与 ：

检验 与 ：

检验 与 ：

当给定 μ0 时，执行具有单侧备择假设的检验：

检验 与 ：

检验 与 ：

MaxIterations  (2)

设置最大迭代次数用于多变量检验：

默认情况下，允许500次迭代：

设置最大迭代次数可能会导致收敛性的缺乏：

值不是相等的：

Method  (3)

默认情况下，使用单变量数据的 BinomialDistribution 计算 值：

对于单变量数据使用渐近方法：

对于对变量数据，只有渐近的结果：

SignificanceLevel  (1)

对于 "TestConclusion" 和 "ShortTestConclusion" 也可使用显著性水平：

应用  (2)

对 8 个病人进行新的睡眠辅助方法检验. 对某个晚上，分别记录每个病人服用药物和服用安慰剂入睡所花的分钟数：

SignTest 没有检测到睡眠辅助药物和安慰剂的不同：

虽然数据集很小，但也通过了正态性检验：

一个效能更好的 PairedTTest 显示服用睡眠辅助药物，入睡所花时间更短：

10 个数学和科学成绩很低的学生被要求参加为期两个星期的强化数学和科学集训项目. 在项目后，举行一个测验，该测验与原考试类似. 这些学生在两次考试的数学和科学部分的得分如下：

整体上看，成绩有显著的提高：

对每个分量的 Bonferroni-corrected 检验，表明数学成绩本身对所检测到的进步起作用：

属性和关系  (6)

从概念上讲，SignTest 计算一个数据集中正号的数目：

对于单变量数据，忽略零，检验统计量服从 BinomialDistribution：

对于定位而言，SignTest 通常没有其它假设检验强大：

对于多变量数据，当计算检验统计量时，使用空间符号：

当空间中位数非零时，空间符号倾向于形成聚类：

聚类的数目由检验统计量计算：

检验统计量服从 ChiSquareDistribution：

对于多变量数据，检验统计量是仿射不变的：

只有当输入是一个 TimeSeries 时，符号检测才会作用于值（values）：

当输入是一个 TemporalData 时，符号检测一起作用于所有值：

只检测所有值：

检测两条路径中位数的差异：

巧妙范例  (2)

当零假设 为真时，计算统计量：

给定特定的备择假设的检验统计量：

比较检验统计量的分布：

三维空间中，空间符号的分布表明：从零均值向量的较大偏离，通常产生更多的高度集中的空间符号和较大的符号统计量：

Wolfram Research (2010)，SignTest，Wolfram 语言函数，https://reference.wolfram.com/language/ref/SignTest.html.

文本

Wolfram Research (2010)，SignTest，Wolfram 语言函数，https://reference.wolfram.com/language/ref/SignTest.html.

CMS

Wolfram 语言. 2010. "SignTest." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/SignTest.html.

APA

Wolfram 语言. (2010). SignTest. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/SignTest.html 年

BibTeX

@misc{reference.wolfram_2024_signtest, author="Wolfram Research", title="{SignTest}", year="2010", howpublished="\url{https://reference.wolfram.com/language/ref/SignTest.html}", note=[Accessed: 03-December-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_signtest, organization={Wolfram Research}, title={SignTest}, year={2010}, url={https://reference.wolfram.com/language/ref/SignTest.html}, note=[Accessed: 03-December-2024 ]}