

TTest
Details and Options



- TTest tests the null hypothesis
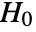 against the alternative hypothesis
against the alternative hypothesis 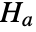 :
: -
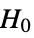
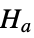
data 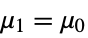
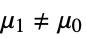
{data1,data2} 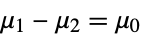
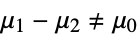
- where μi is the population mean for datai.
- By default, a probability value or
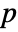 -value is returned.
-value is returned. - A small
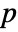 -value suggests that it is unlikely that
-value suggests that it is unlikely that 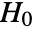 is true.
is true. - The data in dspec can be univariate {x1,x2,…} or multivariate {{x1,y1,…},{x2,y2,…},…}.
- The argument μ0 can be a real number or a real vector with length equal to the dimension of the data.
- TTest assumes that the data is normally distributed but is fairly robust to this assumption. TTest also assumes that the samples are independent in the two sample cases.
- TTest[dspec,μ0,"HypothesisTestData"] returns a HypothesisTestData object htd that can be used to extract additional test results and properties using the form htd["property"].
- TTest[dspec,μ0,"property"] can be used to directly give the value of "property".
- Properties related to the reporting of test results include:
-
"DegreesOfFreedom" the degrees of freedom used in a test "PValue" list of 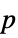 -values
-values"PValueTable" formatted table of 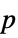 -values
-values"ShortTestConclusion" a short description of the conclusion of a test "TestConclusion" a description of the conclusion of a test "TestData" list of pairs of test statistics and 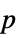 -values
-values"TestDataTable" formatted table of 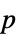 -values and test statistics
-values and test statistics"TestStatistic" list of test statistics "TestStatisticTable" formatted table of test statistics - For univariate samples, TTest performs a Student
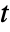 test. The test statistic is assumed to follow a StudentTDistribution[df].
test. The test statistic is assumed to follow a StudentTDistribution[df]. - For multivariate samples, TTest performs Hotelling's
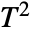 test. The test statistic is assumed to follow a HotellingTSquareDistribution[p,df] where p is the dimension of data.
test. The test statistic is assumed to follow a HotellingTSquareDistribution[p,df] where p is the dimension of data. - The degrees of freedom df, used to specify the distribution of the test statistic, depend on the sample size, number of samples, and in the case of two univariate samples, the results of a test for equal variances.
- The following options can be used:
-
AlternativeHypothesis "Unequal" the inequality for the alternative hypothesis SignificanceLevel 0.05 cutoff for diagnostics and reporting VerifyTestAssumptions Automatic what assumptions to verify - For the TTest, a cutoff
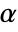 is chosen such that
is chosen such that 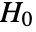 is rejected only if
is rejected only if 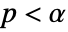 . The value of
. The value of 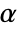 used for the "TestConclusion" and "ShortTestConclusion" properties is controlled by the SignificanceLevel option. This value
used for the "TestConclusion" and "ShortTestConclusion" properties is controlled by the SignificanceLevel option. This value 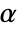 is also used in diagnostic tests of assumptions, including tests for normality, equal variance, and symmetry. By default,
is also used in diagnostic tests of assumptions, including tests for normality, equal variance, and symmetry. By default, 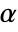 is set to 0.05.
is set to 0.05. - Named settings for VerifyTestAssumptions in TTest include:
-
"Normality" verify that all data is normally distributed "EqualVariance" verify that data1 and data2 have equal variance
Examples
open all close allBasic Examples (3)
Scope (13)
Testing (10)
The ![]() -values are typically large when the mean is close to
-values are typically large when the mean is close to ![]() :
:
The ![]() -values are typically small when the location is far from
-values are typically small when the location is far from ![]() :
:
Using Automatic is equivalent to testing for a mean of zero:
The ![]() -values are typically large when the mean is close to
-values are typically large when the mean is close to ![]() :
:
The ![]() -values are typically small when the location is far from
-values are typically small when the location is far from ![]() :
:
Test whether the mean vector of a multivariate dataset is the zero vector:
Alternatively, test against {0.1,0,–0.05,0}:
The ![]() -values are generally small when the locations are not equal:
-values are generally small when the locations are not equal:
The ![]() -values are generally large when the locations are equal:
-values are generally large when the locations are equal:
The order of the datasets affects the test results:
Test whether the mean difference vector of two multivariate datasets is the zero vector:
Alternatively, test against {1,0,–1,0}:
Create a HypothesisTestData object for repeated property extraction:
The properties available for extraction:
Extract some properties from a HypothesisTestData object:
The ![]() -value, test statistic, and degrees of freedom:
-value, test statistic, and degrees of freedom:
Options (11)
AlternativeHypothesis (3)
SignificanceLevel (2)
VerifyTestAssumptions (6)
By default, normality and equal variance are tested:
If assumptions are not checked, some test results may differ:
Diagnostics can be controlled as a group using All or None:
Diagnostics can be controlled independently:
Assume normality but check for equal variances:
Set the equal variance assumption to False:
Unlisted assumptions are not tested:
The result is the same but a warning is issued:
Bypassing diagnostic tests can save compute time:
It is often useful to bypass diagnostic tests for simulation purposes:
The assumptions of the test hold by design, so a great deal of time can be saved:
Applications (4)
Test whether the means of some populations are equal:
The means of the first two populations are similar:
The mean of the third population is different from the first:
The "third series" of measurements of the passage time of light was recorded by Newcomb in 1882. The given values divided by 1000 plus 24 give the time in millionths of a second for light to traverse a known distance. The true value is now considered to be 33.02:
Use Chauvenet's criterion to identify outlying observations:
A ![]() -test on the bulk of the data suggests that Newcomb's measure of the speed of light was significantly lower than reality:
-test on the bulk of the data suggests that Newcomb's measure of the speed of light was significantly lower than reality:
The vitamin C content and head weight were recorded for 30 samples from each of two experimental cabbage cultivars:
Plots of the head weight and vitamin C content by cultivar:
The vitamin C content is significantly higher for the c52 cultivar:
The weight data is not normally distributed for c52, so MannWhitneyTest is used to show that a significantly lighter cabbage produced significantly more vitamin C:
Fifty samples from each of three species of iris flowers were collected. The samples consist of measures of the length and width of the irises' sepals and petals. It is difficult to distinguish the species virginica and versicolor from one another:
A Hotelling ![]() test suggests a difference in the measures for the two similar species:
test suggests a difference in the measures for the two similar species:
A visualization of the data suggests this difference is most prominent in the petal dimensions:
Properties & Relations (11)
For univariate data, the test statistic follows StudentTDistribution under ![]() :
:
For multivariate data, the test statistic follows HotellingTSquareDistribution under ![]() :
:
The degrees of freedom are data-dependent for univariate data:
Two samples with equal variances:
Two samples with unequal variances (Satterthwaite approximation):
The type of degrees of freedom used can be controlled using VerifyTestAssumptions:
Explicitly assume equal variances and test for normality:
Explicitly assume unequal variances to use the Satterthwaite approximation:
For multivariate data, the squared Mahalanobis distance is used to compute Hotelling's ![]() statistic:
statistic:
Under ![]() , the test statistic follows HotellingTSquareDistribution[p,n-1]:
, the test statistic follows HotellingTSquareDistribution[p,n-1]:
If the population variance is known, the more powerful ZTest can be used:
ZTest correctly rejects ![]() more frequently than TTest:
more frequently than TTest:
TTest is robust to mild deviations from normality:
The ![]() -value can still be interpreted in the usual way:
-value can still be interpreted in the usual way:
Large deviations from normality require the use of median-based tests:
The ![]() -value can be interpreted in the usual way for SignedRankTest but not TTest:
-value can be interpreted in the usual way for SignedRankTest but not TTest:
For two-sample testing of non-normal data, use MannWhitneyTest:
For non-normal data, MannWhitneyTest can be more powerful than TTest:
TTest works with the values only when the input is a TimeSeries:
TTest works with all the values together when the input is a TemporalData:
Possible Issues (2)
TTest assumes that the data is normally distributed:
Use a median-based test that does not assume normality:
The covariance matrix of multivariate data may not be invertible:
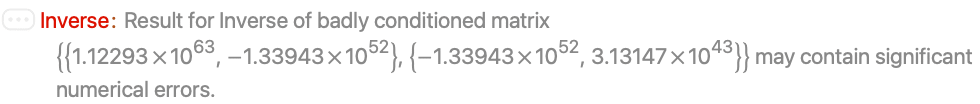
Related Guides
History
Text
Wolfram Research (2010), TTest, Wolfram Language function, https://reference.wolfram.com/language/ref/TTest.html.
CMS
Wolfram Language. 2010. "TTest." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/TTest.html.
APA
Wolfram Language. (2010). TTest. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/TTest.html
BibTeX
@misc{reference.wolfram_2025_ttest, author="Wolfram Research", title="{TTest}", year="2010", howpublished="\url{https://reference.wolfram.com/language/ref/TTest.html}", note=[Accessed: 06-January-2026]}
BibLaTeX
@online{reference.wolfram_2025_ttest, organization={Wolfram Research}, title={TTest}, year={2010}, url={https://reference.wolfram.com/language/ref/TTest.html}, note=[Accessed: 06-January-2026]}