SignTest

SignTest[data]

tests whether the median of data is zero.

SignTest[{data1,data2}]

tests whether the median of data1– data2 is zero.

SignTest[dspec,μ0]

tests a location measure against μ0.

SignTest[dspec,μ0,"property"]

returns the value of "property".

Details and Options

  • SignTest tests the null hypothesis 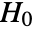against the alternative hypothesis :
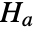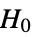
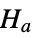
  • data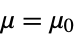
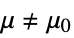
    {data1,data2}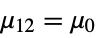
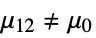
  • where μ is the population median for data and μ12 is the median of the paired differences of the two datasets .
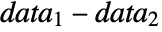  • By default, a probability value or 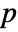-value is returned.
  • A small 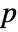-value suggests that it is unlikely that 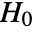is true.
  • The data in dspec can be univariate {x1,x2,…} or multivariate {{x1,y1,…},{x2,y2,…},…}.
  • If two samples are given, they must be of equal length.
  • The argument μ0 can be a real number or a real vector with length equal to the dimension of the data.
  • SignTest[dspec,μ0,"HypothesisTestData"] returns a HypothesisTestData object htd that can be used to extract additional test results and properties using the form htd["property"].
  • SignTest[dspec,μ0,"property"] can be used to directly give the value of "property".
  • Properties related to the reporting of test results include:
  • "DegreesOfFreedom"the degrees of freedom used in a test
    "PValue"list of 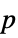-values
    "PValueTable"formatted table of 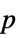-values
    "ShortTestConclusion"a short description of the conclusion of a test
    "TestConclusion"a description of the conclusion of a test
    "TestData"list of pairs of test statistics and 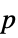-values
    "TestDataTable"formatted table of 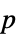-values and test statistics
    "TestStatistic"list of test statistics
    "TestStatisticTable"formatted table of test statistics
  • For univariate samples, SignTest performs the sign test for medians of paired samples. The test statistic is assumed to follow a BinomialDistribution[n,1/2] where n is the number of elements in dspec not equal to μ0.
  • For multivariate samples, SignTest performs an affine invariant test for paired samples using spatial signs. The test statistic is assumed to follow a ChiSquareDistribution[dim] where dim is the dimension of dspec.
  • The following options can be used:
  • AlternativeHypothesis "Unequal"the inequality for the alternative hypothesis
    MaxIterations Automaticmax iterations for multivariate median tests
    Method Automaticthe method to use for computing 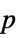-values
    SignificanceLevel 0.05cutoff for diagnostics and reporting
  • For the SignTest, a cutoff 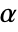is chosen such that 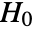is rejected only if 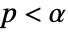. The value of 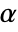used for the "TestConclusion" and "ShortTestConclusion" properties is controlled by the SignificanceLevel option. By default, 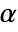is set to 0.05.

Examples

open allclose all

Basic Examples  (4)

Test whether the median of a population is zero:

Test whether the spatial median of a multivariate population is some value:

Compute the test statistic:

Compare the median difference for paired data to a particular value:

Report the test results in a table:

Create a HypothesisTestData object for repeated property extraction:

A list of available properties:

Extract a single property or a list of properties:

Scope  (13)

Testing  (10)

Test versus :

The -values are typically large when the median is close to μ0:

The -values are typically small when the location is far from μ0:

Using Automatic is equivalent to testing for a median of zero:

Test versus :

The -values are typically large when the median is close to μ0:

The -values are typically small when the location is far from μ0:

Test whether the median vector of a multivariate population is the zero vector:

Alternatively, test against {0.1,0,-0.05,0}:

Test versus :

The -values are generally small when the locations are not equal:

The -values are generally large when the locations are equal:

Test versus :

The order of the datasets affects the test results:

Test whether the median difference vector of two multivariate populations is the zero vector:

Alternatively, test against {1,0,-1,0}:

Create a HypothesisTestData object for repeated property extraction:

The properties available for extraction:

Extract some properties from a HypothesisTestData object:

The -value and test statistic:

Extract any number of properties simultaneously:

The -value and test statistic:

Reporting  (3)

Tabulate the test results:

Retrieve the entries from a test table for customized reporting:

Tabulate -values or test statistics:

The -value from the table:

The test statistic from the table:

Options  (9)

AlternativeHypothesis  (3)

A two-sided test is performed by default:

Test versus :

Perform a two-sided test or a one-sided alternative:

Test versus :

Test versus :

Test versus :

Perform tests with one-sided alternatives when μ0 is given:

Test versus :

Test versus :

MaxIterations  (2)

Set the maximum number of iterations to use for multivariate tests:

By default, 500 iterations are allowed:

Setting the maximum number of iterations may result in lack of convergence:

The -values are not equivalent:

Method  (3)

By default, -values are computed using the BinomialDistribution for univariate data:

Asymptotic methods can be used for univariate data:

For multivariate data, only the asymptotic result is available:

SignificanceLevel  (1)

The significance level is also used for "TestConclusion" and "ShortTestConclusion":

Applications  (2)

A new sleeping aid was tested on eight patients. The number of minutes taken for each subject to fall asleep was recorded for a night taking the medication and for a night with a placebo:

The SignTest does not detect a difference in the sleep aid and placebo:

The datasets, while very small, do not fail a test for normality:

A more powerful PairedTTest shows a significant reduction in time to sleep with the sleep aid:

A group of 10 students with low assessments in mathematics and science was asked to participate in tutoring program. A test similar to the original assessment was administered after the program. The students' scores on the math and science portions of both assessments are as follows:

There is a significant improvement in scores overall:

The Bonferroni-corrected tests of the individual components suggest that math scores alone account for the detected improvement:

Properties & Relations  (6)

Conceptually, the SignTest counts the number of positive signs in a dataset:

For univariate data, the test statistic follows a BinomialDistribution, ignoring zeros:

The SignTest is generally less powerful than other hypothesis tests for location:

For multivariate data, spatial signs are used when computing the test statistic:

Spatial signs tend to cluster when the spatial median is nonzero:

The amount of clustering is quantified by the test statistic:

The test statistic follows a ChiSquareDistribution[p]:

The test statistic is affine invariant for multivariate data:

The sign test works with the values only when the input is a TimeSeries:

The sign test works with all the values together when the input is a TemporalData:

Test all the values only:

Test the difference of the medians of the two paths:

Neat Examples  (2)

Compute the statistic when the null hypothesis is true:

The test statistic given a particular alternative:

Compare the distributions of the test statistics:

The distribution of spatial signs in three dimensions shows that larger deviations from a zero mean vector produce more highly clustered spatial signs and larger sign statistics:

Wolfram Research (2010), SignTest, Wolfram Language function, https://reference.wolfram.com/language/ref/SignTest.html.

Text

Wolfram Research (2010), SignTest, Wolfram Language function, https://reference.wolfram.com/language/ref/SignTest.html.

CMS

Wolfram Language. 2010. "SignTest." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/SignTest.html.

APA

Wolfram Language. (2010). SignTest. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/SignTest.html

BibTeX

@misc{reference.wolfram_2024_signtest, author="Wolfram Research", title="{SignTest}", year="2010", howpublished="\url{https://reference.wolfram.com/language/ref/SignTest.html}", note=[Accessed: 22-December-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_signtest, organization={Wolfram Research}, title={SignTest}, year={2010}, url={https://reference.wolfram.com/language/ref/SignTest.html}, note=[Accessed: 22-December-2024 ]}