PairedTTest

PairedTTest[data]

tests whether the mean of data is zero.

PairedTTest[{data1,data2}]

tests whether the mean of data1– data2 is zero.

PairedTTest[dspec,μ0]

tests a location measure against μ0.

PairedTTest[dspec,μ0,"property"]

returns the value of "property".

Details and Options

  • PairedTTest tests the null hypothesis 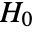against the alternative hypothesis :
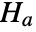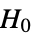
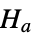
  • data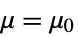
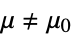
    {data1,data2}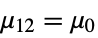
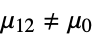
  • where μ is the population mean for data and μ12 is the mean of the paired differences of the two datasets .
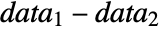  • By default, a probability value or 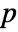-value is returned.
  • A small 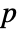-value suggests that it is unlikely that 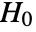is true.
  • The data in dspec can be univariate {x1,x2,…} or multivariate {{x1,y1,…},{x2,y2,…},…}.
  • If two samples are given, they must be of equal length.
  • The argument μ0 can be a real number or a real vector with length equal to the dimension of the data.
  • PairedTTest[dspec,μ0,"HypothesisTestData"] returns a HypothesisTestData object htd that can be used to extract additional test results and properties using the form htd["property"].
  • PairedTTest[dspec,μ0,"property"] can be used to directly give the value of "property".
  • Properties related to the reporting of test results include:
  • "DegreesOfFreedom"the degrees of freedom used in a test
    "PValue"list of 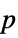-values
    "PValueTable"formatted table of 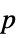-values
    "ShortTestConclusion"a short description of the conclusion of a test
    "TestConclusion"a description of the conclusion of a test
    "TestData"list of pairs of test statistics and 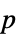-values
    "TestDataTable"formatted table of 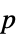-values and test statistics
    "TestStatistic"list of test statistics
    "TestStatisticTable"formatted table of test statistics
  • PairedTTest is more powerful than the TTest when samples are matched.
  • For univariate samples, PairedTTest performs the Student 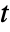test for matched pairs. The test statistic is assumed to follow a StudentTDistribution.
  • For multivariate samples, PairedTTest performs Hotelling's 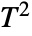test for matched pairs. The test statistic is assumed to follow a HotellingTSquareDistribution.
  • The following options can be used:
  • AlternativeHypothesis "Unequal"the inequality for the alternative hypothesis
    SignificanceLevel 0.05cutoff for diagnostics and reporting
    VerifyTestAssumptions Automaticwhat assumptions to verify
  • For the PairedTTest, a cutoff 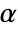is chosen such that 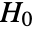is rejected only if 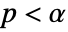. The value of 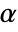used for the "TestConclusion" and "ShortTestConclusion" properties is controlled by the SignificanceLevel option. This value 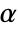is also used in diagnostic tests of assumptions, including tests for normality, equal variance, and symmetry. By default, 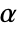is set to 0.05.
  • Named settings for VerifyTestAssumptions in PairedTTest include:
  • "Normality"verify that all data is normally distributed

Examples

open allclose all

Basic Examples  (3)

Test whether the mean of a population is zero:

The full test table:

Test whether the means of two dependent populations differ:

The mean of the differences:

At the 0.05 level, the mean of the differenced data is not significantly different from 0:

Compare the locations of dependent multivariate populations:

The mean of the differences:

At the 0.05 level, the mean of the differenced data is not significantly different from 0:

Scope  (13)

Testing  (10)

Test versus :

The -values are typically large when the mean is close to μ0:

The -values are typically small when the location is far from μ0:

Using Automatic is equivalent to testing for a mean of zero:

Test versus :

The -values are typically large when the mean is close to μ0:

The -values are typically small when the location is far from μ0:

Test whether the mean vector of a multivariate population is the zero vector:

Alternatively, test against {0.1,0,-0.05,0}:

Test whether the mean of differenced datasets is zero:

The -values are generally small when the mean is not zero:

The -values are generally large when the mean is zero:

Test whether the mean of differenced data is 3:

The order of the datasets affects the test results:

Test whether the mean vector of differenced multivariate data is the zero vector:

Alternatively, test against {1,0,-1,0}:

Create a HypothesisTestData object for repeated property extraction:

The properties available for extraction:

Extract some properties from a HypothesisTestData object:

The -value, test statistic, and degrees of freedom:

Extract any number of properties simultaneously:

The -value, test statistic, and degrees of freedom:

Reporting  (3)

Tabulate the test results:

Retrieve the entries from a test table for customized reporting:

Tabulate -values or test statistics:

The -value from the table:

The test statistic from the table:

Options  (8)

AlternativeHypothesis  (3)

A two-sided test is performed by default:

Test versus :

Perform a two-sided test or a one-sided alternative:

Test versus :

Test versus :

Test versus :

Perform tests with one-sided alternatives when μ0 is given:

Test versus :

Test versus :

SignificanceLevel  (2)

Set the significance level for diagnostic tests:

By default, 0.05 is used:

The significance level is also used for "TestConclusion" and "ShortTestConclusion":

VerifyTestAssumptions  (3)

By default, normality is tested:

Here normality is assumed:

The result is the same, but a warning is issued:

Alternatively, use All:

Set the normality assumption to True:

Bypassing diagnostic tests can save compute time:

It is often useful to bypass diagnostic tests for simulation purposes:

The assumptions of the test hold by design, so a great deal of time can be saved:

The results are identical:

Applications  (1)

A group of 15 students is convinced that they were more prepared for the mathematics portion of the ACT than that of the SAT. Test this claim assuming that national ACT and SAT scores are normally distributed with means 21.7 and 528.5 and standard deviations 4.1 and 117.2, respectively:

For comparison, the data should be normalized:

Density estimates for the individual and differenced scores:

can be rejected at the 5% level. The students' claim is not refuted:

Properties & Relations  (6)

PairedTTest is equivalent to a TTest for a single dataset:

For two datasets, the PairedTTest is equivalent to a TTest of the paired differences:

If the variance of the population is known, the more powerful PairedZTest can be used:

The probability that the PairedZTest will return a -value smaller than the PairedTTest:

If the data can be paired, the PairedTTest is more powerful than the TTest:

The paired test detects a significant difference where the unpaired test does not:

The paired test works with the values only when the input is a TimeSeries:

The paired test works with all the values together when the input is a TemporalData:

Test all the values only:

Test the difference of the means of the two paths:

Possible Issues  (1)

PairedTTest requires that the data be normally distributed:

Use a median-based test instead:

Neat Examples  (1)

Compute the statistic when the null hypothesis is true:

The test statistic given a particular alternative:

Compare the distributions of the test statistics:

Wolfram Research (2010), PairedTTest, Wolfram Language function, https://reference.wolfram.com/language/ref/PairedTTest.html.

Text

Wolfram Research (2010), PairedTTest, Wolfram Language function, https://reference.wolfram.com/language/ref/PairedTTest.html.

CMS

Wolfram Language. 2010. "PairedTTest." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/PairedTTest.html.

APA

Wolfram Language. (2010). PairedTTest. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/PairedTTest.html

BibTeX

@misc{reference.wolfram_2024_pairedttest, author="Wolfram Research", title="{PairedTTest}", year="2010", howpublished="\url{https://reference.wolfram.com/language/ref/PairedTTest.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_pairedttest, organization={Wolfram Research}, title={PairedTTest}, year={2010}, url={https://reference.wolfram.com/language/ref/PairedTTest.html}, note=[Accessed: 21-November-2024 ]}