SolidMechanicsPDEComponent
SolidMechanicsPDEComponent[vars,pars]
変数 vars,パラメータ pars の固体力学の偏微分方程式の項を与える.
詳細


- SolidMechanicsPDEComponentは,固体力学解析のための偏微分方程式を返す.
- SolidMechanicsPDEComponentは,偏微分方程式の部分として使われる微分演算子の和を返す.
- SolidMechanicsPDEComponentは,加えられた荷重と拘束を受ける物体の結果の変位をモデル化する.
- SolidMechanicsPDEComponentは,定常,時間依存,パラメトリック,周波数応答,固有モードの各分析のための偏微分方程式の成分を作成する.
- SolidMechanicsPDEComponentは,従属変数としての変位
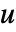 ,
,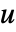 ,
,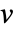 (単位:[
(単位:[![TemplateBox[{InterpretationBox[, 1], "m", meters, "Meters"}, QuantityTF] TemplateBox[{InterpretationBox[, 1], "m", meters, "Meters"}, QuantityTF]](Files/SolidMechanicsPDEComponent.ja/6.png) ]),独立変数
]),独立変数 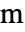 (単位:[
(単位:[![TemplateBox[{InterpretationBox[, 1], "m", meters, "Meters"}, QuantityTF] TemplateBox[{InterpretationBox[, 1], "m", meters, "Meters"}, QuantityTF]](Files/SolidMechanicsPDEComponent.ja/8.png) ]),時間変数
]),時間変数 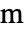 (単位:秒 [
(単位:秒 [![TemplateBox[{InterpretationBox[, 1], "s", seconds, "Seconds"}, QuantityTF] TemplateBox[{InterpretationBox[, 1], "s", seconds, "Seconds"}, QuantityTF]](Files/SolidMechanicsPDEComponent.ja/10.png) ]),角周波数
]),角周波数 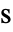 (単位:ラジアン毎秒)で固体力学現象をモデル化する.
(単位:ラジアン毎秒)で固体力学現象をモデル化する. - SolidMechanicsPDEComponentは2Dおよび3Dで偏微分方程式成分を作成する.
- 定常変数 vars は vars={{u[x1,…,xn],v[x1,…,xn],…},{x1,…,xn}}である.
- 時間依存変数または固有モード変数の vars は vars={{u[t,x1,…,xn],v[t,x1,…,xn],…},t,{x1,…,xn}}である.
- 周波数依存変数 vars は vars={{u[x1,…,xn],v[x1,…,xn],…},ω,{x1,…,xn}}である.
- 異なる解析タイプのための方程式SolidMechanicsPDEComponentは vars の形式によって生成される.
- 質量密度
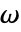 [
[![TemplateBox[{InterpretationBox[, 1], {"kg", , "/", , {"m", ^, 3}}, kilograms per meter cubed, {{(, "Kilograms", )}, /, {(, {"Meters", ^, 3}, )}}}, QuantityTF] TemplateBox[{InterpretationBox[, 1], {"kg", , "/", , {"m", ^, 3}}, kilograms per meter cubed, {{(, "Kilograms", )}, /, {(, {"Meters", ^, 3}, )}}}, QuantityTF]](Files/SolidMechanicsPDEComponent.ja/13.png) ],応力テンソル
],応力テンソル 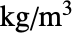 [
[![TemplateBox[{InterpretationBox[, 1], "Pa", pascals, "Pascals"}, QuantityTF] TemplateBox[{InterpretationBox[, 1], "Pa", pascals, "Pascals"}, QuantityTF]](Files/SolidMechanicsPDEComponent.ja/15.png) ],歪みテンソル
],歪みテンソル 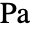 ,変位ベクトル
,変位ベクトル 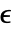 [
[![TemplateBox[{InterpretationBox[, 1], "m", meters, "Meters"}, QuantityTF] TemplateBox[{InterpretationBox[, 1], "m", meters, "Meters"}, QuantityTF]](Files/SolidMechanicsPDEComponent.ja/18.png) ],物体荷重ベクトル
],物体荷重ベクトル 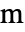 [
[![TemplateBox[{InterpretationBox[, 1], {"N", , "/", , {"m", ^, 3}}, newtons per meter cubed, {{(, "Newtons", )}, /, {(, {"Meters", ^, 3}, )}}}, QuantityTF] TemplateBox[{InterpretationBox[, 1], {"N", , "/", , {"m", ^, 3}}, newtons per meter cubed, {{(, "Newtons", )}, /, {(, {"Meters", ^, 3}, )}}}, QuantityTF]](Files/SolidMechanicsPDEComponent.ja/20.png) ]または
]または 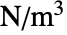 [
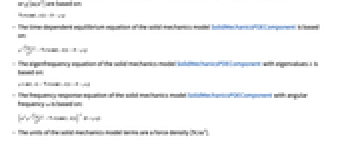
[![TemplateBox[{InterpretationBox[, 1], {"m", , "/", , {"s", ^, 2}}, meters per second squared, {{(, "Meters", )}, /, {(, {"Seconds", ^, 2}, )}}}, QuantityTF] TemplateBox[{InterpretationBox[, 1], {"m", , "/", , {"s", ^, 2}}, meters per second squared, {{(, "Meters", )}, /, {(, {"Seconds", ^, 2}, )}}}, QuantityTF]](Files/SolidMechanicsPDEComponent.ja/22.png) ]の固体力学の偏微分方程式SolidMechanicsPDEComponentの定常平衡方程式は以下に基づく.
]の固体力学の偏微分方程式SolidMechanicsPDEComponentの定常平衡方程式は以下に基づく. - 固体力学モデルSolidMechanicsPDEComponentの時間依存平衡方程式は以下に基づく.
- 固有値が
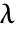 の固体力学モデルSolidMechanicsPDEComponentの固有周波数方程式は以下に基づく.
の固体力学モデルSolidMechanicsPDEComponentの固有周波数方程式は以下に基づく. - 角周波数
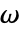 の固体力学モデルSolidMechanicsPDEComponentの周波数応答方程式は以下に基づく.
の固体力学モデルSolidMechanicsPDEComponentの周波数応答方程式は以下に基づく. - 固体力学モデル項の単位は力密度(単位:
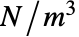 )である.
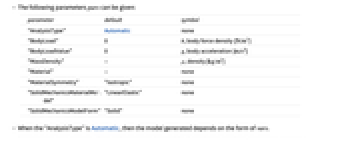
)である. - 次のパラメータ pars を与えることができる.
-
パラメータ デフォルト シンボル "AnalysisType" Automatic なし "BodyLoad" 0 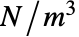 ,体積力密度(単位:[
,体積力密度(単位:[![TemplateBox[{InterpretationBox[, 1], {"N", , "/", , {"m", ^, 3}}, newtons per meter cubed, {{(, "Newtons", )}, /, {(, {"Meters", ^, 3}, )}}}, QuantityTF] TemplateBox[{InterpretationBox[, 1], {"N", , "/", , {"m", ^, 3}}, newtons per meter cubed, {{(, "Newtons", )}, /, {(, {"Meters", ^, 3}, )}}}, QuantityTF]](Files/SolidMechanicsPDEComponent.ja/31.png) ]
]
"BodyLoadValue" 0 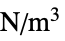 ,体加速度(単位:[
,体加速度(単位:[![TemplateBox[{InterpretationBox[, 1], {"m", , "/", , {"s", ^, 2}}, meters per second squared, {{(, "Meters", )}, /, {(, {"Seconds", ^, 2}, )}}}, QuantityTF] TemplateBox[{InterpretationBox[, 1], {"m", , "/", , {"s", ^, 2}}, meters per second squared, {{(, "Meters", )}, /, {(, {"Seconds", ^, 2}, )}}}, QuantityTF]](Files/SolidMechanicsPDEComponent.ja/33.png) ]
]
"MassDensity" - 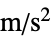 ,密度(単位:[
,密度(単位:[![TemplateBox[{InterpretationBox[, 1], {"kg", , "/", , {"m", ^, 3}}, kilograms per meter cubed, {{(, "Kilograms", )}, /, {(, {"Meters", ^, 3}, )}}}, QuantityTF] TemplateBox[{InterpretationBox[, 1], {"kg", , "/", , {"m", ^, 3}}, kilograms per meter cubed, {{(, "Kilograms", )}, /, {(, {"Meters", ^, 3}, )}}}, QuantityTF]](Files/SolidMechanicsPDEComponent.ja/35.png) ]
]
"Material" - なし "MaterialSymmetry" "Isotropic" なし "SolidMechanicsMaterialModel" "LinearElastic" なし "SolidMechanicsModelForm" "Solid" なし - "AnalysisType"がAutomaticなら,生成されるモデルは vars の形式に依存する.
- 固有周波数解析については,"AnalysisType"を"Eigenmode"に設定し,時間依存変数 tvars を使う必要がある.
- "Material"が指定されているなら,材料定数は材料データから抽出される.それ以外の場合は関連する材料パラメータを指定しなければならない.
- 線形弾性等方性材料については,任意の2つの係数が使用できる.
-
パラメータ名 "BulkModulus" "LameParameter" "PoissonRatio" "PWaveModulus" "ShearModulus" "YoungModulus" - パラメータ"SolidMechanicsModelForm"は,"Solid","PlaneStress","PlaneStrain","ExtendedPlaneStress","ExtendedPlaneStrain"のいずれかでよい.
- "PlaneStress","PlaneStrain","ExtendedPlaneStress","ExtendedPlaneStrain"の各モデルについては,"Thickness"パラメータを定義しなければならない.
- デフォルトの材料モデルは線形弾性等方性材料モデルである.
- 線形弾性で小さな変形があるモデルについて,次の材料対称性が使用可能である.
-
材料対称性名 "Isotropic" "Orthotropic" "TransverselyIsotropic" "Anisotropic" - 次の等方性可縮超弾性の大きく変形する材料モデルが利用できる.
-
材料モデル名 "StVenantKirchhoff" "NeoHookean" - 次のほぼ等方性非可縮超弾性の大きく変形する材料モデルが利用できる.
-
材料モデル名 "ArrudaBoyce" "Gent" "MooneyRivlin" "NeoHookean" "Yeoh" - 運動方程式は,微量な小さい変形歪み測定値を使用する.
- 非線形材料法則の場合は,運動方程式は変形勾配
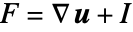 に基づいてグリーン・ラグランジュ(Green–Lagrange)歪みの測定値を使う.ここで,
に基づいてグリーン・ラグランジュ(Green–Lagrange)歪みの測定値を使う.ここで,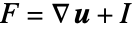 は恒等行列である.
は恒等行列である. - 弾性行列
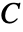 ,初期応力
,初期応力 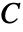 ,初期歪み
,初期歪み 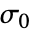 ,熱歪み
,熱歪み 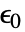 の線形弾性材料モデルの構成方程式は以下で与えられる.
の線形弾性材料モデルの構成方程式は以下で与えられる. - 垂直歪み成分
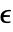 とせん断歪み成分
とせん断歪み成分 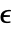 は次の次数のフォークト(Voigt)記法を使う.
は次の次数のフォークト(Voigt)記法を使う. - 垂直応力成分
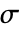 とせん断応力成分
とせん断応力成分 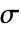 は次の次数のフォークト(Voigt)記法を使う.
は次の次数のフォークト(Voigt)記法を使う. - "PlaneStrain"モデルは
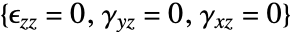 について
について 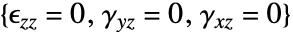 方向の歪みが0であると仮定する.
方向の歪みが0であると仮定する. - "PlaneStress"モデルは
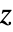 について
について 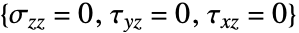 方向の応力が0であると仮定する.
方向の応力が0であると仮定する. - "RegionSymmetry""Axisymmetric"は切頂円筒座標系を使い,
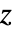 方向に
方向に 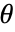 の変位があって
の変位があって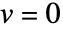 であると仮定する.
であると仮定する.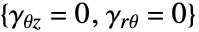 である点に注意のこと.
である点に注意のこと. - ヤング率
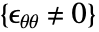 ,ポアソン比
,ポアソン比 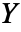 の線形弾性等方性材料についての構成方程式は以下で与えられる.
の線形弾性等方性材料についての構成方程式は以下で与えられる. - 熱歪み
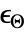 は,熱膨張係数
は,熱膨張係数 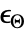 (単位:[
(単位:[![1TemplateBox[{InterpretationBox[, 1], {"/", , "K"}, reciprocal kelvins, {1, /, {(, "Kelvins", )}}}, QuantityTF] 1TemplateBox[{InterpretationBox[, 1], {"/", , "K"}, reciprocal kelvins, {1, /, {(, "Kelvins", )}}}, QuantityTF]](Files/SolidMechanicsPDEComponent.ja/64.png) ]),熱歪み温度
]),熱歪み温度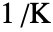 (単位:[
(単位:[![TemplateBox[{InterpretationBox[, 1], "K", kelvins, "Kelvins"}, QuantityTF] TemplateBox[{InterpretationBox[, 1], "K", kelvins, "Kelvins"}, QuantityTF]](Files/SolidMechanicsPDEComponent.ja/66.png) ]),熱歪み参照温度
]),熱歪み参照温度 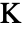 (単位:[
(単位:[![TemplateBox[{InterpretationBox[, 1], "K", kelvins, "Kelvins"}, QuantityTF] TemplateBox[{InterpretationBox[, 1], "K", kelvins, "Kelvins"}, QuantityTF]](Files/SolidMechanicsPDEComponent.ja/68.png) ])で加えることができる.
])で加えることができる. - "LinearElastic" "Isotropic"材料モデルには,次のサブパラメータが使用できる.
-
パラメータ デフォルト シンボル "InitialStrain" 0 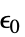 ,初期歪み
,初期歪み"InitialStress" 0 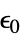 ,初期応力(単位:[
,初期応力(単位:[![TemplateBox[{InterpretationBox[, 1], "Pa", pascals, "Pascals"}, QuantityTF] TemplateBox[{InterpretationBox[, 1], "Pa", pascals, "Pascals"}, QuantityTF]](Files/SolidMechanicsPDEComponent.ja/72.png) ])
])"PoissonRatio" Automatic 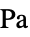 ,ポアソン比
,ポアソン比"ThermalExpansion" 0 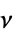 ,熱膨張係数(単位:[
,熱膨張係数(単位:[![1TemplateBox[{InterpretationBox[, 1], {"/", , "K"}, reciprocal kelvins, {1, /, {(, "Kelvins", )}}}, QuantityTF] 1TemplateBox[{InterpretationBox[, 1], {"/", , "K"}, reciprocal kelvins, {1, /, {(, "Kelvins", )}}}, QuantityTF]](Files/SolidMechanicsPDEComponent.ja/75.png) ])
])"ThermalStrainTemperature" 0 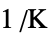 ,温度(単位:[
,温度(単位:[![TemplateBox[{InterpretationBox[, 1], "K", kelvins, "Kelvins"}, QuantityTF] TemplateBox[{InterpretationBox[, 1], "K", kelvins, "Kelvins"}, QuantityTF]](Files/SolidMechanicsPDEComponent.ja/77.png) ])
])"ThermalStrainReferenceTemperature" 0 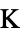 ,温度(単位:[
,温度(単位:[![TemplateBox[{InterpretationBox[, 1], "K", kelvins, "Kelvins"}, QuantityTF] TemplateBox[{InterpretationBox[, 1], "K", kelvins, "Kelvins"}, QuantityTF]](Files/SolidMechanicsPDEComponent.ja/79.png) ])
])"YoungModulus" Automatic 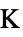 ,ヤング率(単位:[
,ヤング率(単位:[![TemplateBox[{InterpretationBox[, 1], "Pa", pascals, "Pascals"}, QuantityTF] TemplateBox[{InterpretationBox[, 1], "Pa", pascals, "Pascals"}, QuantityTF]](Files/SolidMechanicsPDEComponent.ja/81.png) ])
]) - コンプライアンス行列
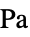 を含む線形弾性直交異方性材料モデルの構成式は以下で与えられる.
を含む線形弾性直交異方性材料モデルの構成式は以下で与えられる. - 弾性行列はコンプライアンス行列
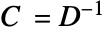 の逆行列である.
の逆行列である. - せん断弾性率が
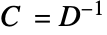 の線形弾性直交異方性コンプライアンス行列
の線形弾性直交異方性コンプライアンス行列 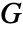 は以下で与えられる.
は以下で与えられる. - 線形弾性直交異方性材料モデルについては,熱弾性係数
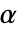 は方向に依存する.
は方向に依存する. - "LinearElastic" "Orthotropic"材料モデルには次のサブパラメータを使うことができる.
-
パラメータ デフォルト シンボル "InitialStrain" 0 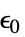 ,初期歪み
,初期歪み"InitialStress" 0 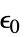 ,初期応力(単位:[
,初期応力(単位:[![TemplateBox[{InterpretationBox[, 1], "Pa", pascals, "Pascals"}, QuantityTF] TemplateBox[{InterpretationBox[, 1], "Pa", pascals, "Pascals"}, QuantityTF]](Files/SolidMechanicsPDEComponent.ja/92.png) ])
])"PoissonRatio" - 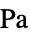 ,
, 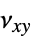 ,
, 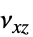 ,
, 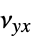 ,
, 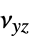 ,
, 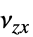 ポアソン比
ポアソン比"ShearModulus" - 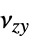 ,
, 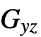 ,
, 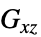 剛性率(単位:[
剛性率(単位:[![TemplateBox[{InterpretationBox[, 1], "Pa", pascals, "Pascals"}, QuantityTF] TemplateBox[{InterpretationBox[, 1], "Pa", pascals, "Pascals"}, QuantityTF]](Files/SolidMechanicsPDEComponent.ja/102.png) ])
])"ThermalExpansion" 0 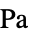 ,
, 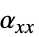 ,
, 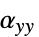 熱膨張係数(単位:[
熱膨張係数(単位:[![TemplateBox[{{InterpretationBox[, 1], 1}, {"/", , "K"}, reciprocal kelvins, {1, /, {(, "Kelvins", )}}}, QuantityTF] TemplateBox[{{InterpretationBox[, 1], 1}, {"/", , "K"}, reciprocal kelvins, {1, /, {(, "Kelvins", )}}}, QuantityTF]](Files/SolidMechanicsPDEComponent.ja/106.png) ])
])"ThermalStrainTemperature" 0 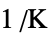 ,温度(単位:[
,温度(単位:[![TemplateBox[{InterpretationBox[, 1], "K", kelvins, "Kelvins"}, QuantityTF] TemplateBox[{InterpretationBox[, 1], "K", kelvins, "Kelvins"}, QuantityTF]](Files/SolidMechanicsPDEComponent.ja/108.png) ])
])"ThermalStrainReferenceTemperature" 0 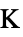 ,温度(単位:[
,温度(単位:[![TemplateBox[{InterpretationBox[, 1], "K", kelvins, "Kelvins"}, QuantityTF] TemplateBox[{InterpretationBox[, 1], "K", kelvins, "Kelvins"}, QuantityTF]](Files/SolidMechanicsPDEComponent.ja/110.png) ])
])"YoungModulus" - 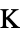 ,
, 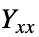 ,
, 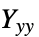 ,ヤング率(単位:[
,ヤング率(単位:[![TemplateBox[{InterpretationBox[, 1], "Pa", pascals, "Pascals"}, QuantityTF] TemplateBox[{InterpretationBox[, 1], "Pa", pascals, "Pascals"}, QuantityTF]](Files/SolidMechanicsPDEComponent.ja/114.png) ])
]) - ポアソン(Poisson)比,剛性率,ヤング(Young)率は指標付きの形式変数として指定される.
- 異方性材料モデルについては,完全弾性行列
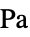 を指定しなければならない.
を指定しなければならない. - 代りにコンプライアンス行列
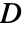 を指定してもよい.
を指定してもよい. - 線形弾性異方性材料モデルについては,熱膨張
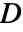 の係数は方向に依存する.
の係数は方向に依存する. - "LinearElastic" "Anisotropic"材料モードについては次のサブパラメータを使うことができる.
-
パラメータ デフォルト シンボル "ComplianceMatrix" - 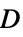 ,コンプライアンス行列
,コンプライアンス行列"ElasticityMatrix" - 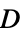 ,弾性行列
,弾性行列 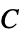
"InitialStrain" 0 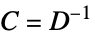 ,初期歪み
,初期歪み"InitialStress" 0 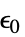 ,初期応力(単位:[
,初期応力(単位:[![TemplateBox[{InterpretationBox[, 1], "Pa", pascals, "Pascals"}, QuantityTF] TemplateBox[{InterpretationBox[, 1], "Pa", pascals, "Pascals"}, QuantityTF]](Files/SolidMechanicsPDEComponent.ja/125.png) ])
])"ThermalExpansion" 0 熱膨張係数 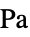 ,
, 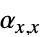 ,
, 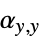 ,
, 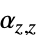 ,
, 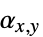 ,
,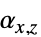 (単位: [
(単位: [![TemplateBox[{{InterpretationBox[, 1], 1}, {"/", , "K"}, reciprocal kelvins, {1, /, {(, "Kelvins", )}}}, QuantityTF] TemplateBox[{{InterpretationBox[, 1], 1}, {"/", , "K"}, reciprocal kelvins, {1, /, {(, "Kelvins", )}}}, QuantityTF]](Files/SolidMechanicsPDEComponent.ja/132.png) ])
])"ThermalStrainTemperature" 0 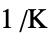 ,温度(単位:[
,温度(単位:[![TemplateBox[{InterpretationBox[, 1], "K", kelvins, "Kelvins"}, QuantityTF] TemplateBox[{InterpretationBox[, 1], "K", kelvins, "Kelvins"}, QuantityTF]](Files/SolidMechanicsPDEComponent.ja/134.png) ])
])"ThermalStrainReferenceTemperature" 0 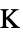 ,温度(単位:[
,温度(単位:[![TemplateBox[{InterpretationBox[, 1], "K", kelvins, "Kelvins"}, QuantityTF] TemplateBox[{InterpretationBox[, 1], "K", kelvins, "Kelvins"}, QuantityTF]](Files/SolidMechanicsPDEComponent.ja/136.png) ])
]) - 圧縮性およびほぼ非圧縮性の超弾性材料モデルが使用可能である.使用可能な場合は,ほぼ非圧縮性のモデルがデフォルトである.
- "ArrudaBoyce"材料モデルはエネルギー密度関数
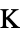 に基づいている.ただし,
に基づいている.ただし,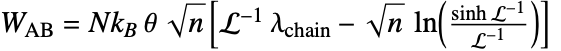 はネットワーク中のポリマー鎖の数,
はネットワーク中のポリマー鎖の数,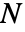 は単一の鎖内のセグメントの数,
は単一の鎖内のセグメントの数,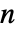 はボルツマン定数,
はボルツマン定数,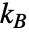 は絶対温度,
は絶対温度,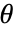 は鎖のストレッチ,
は鎖のストレッチ,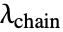 はランジュバン(Langevin)関数である.
はランジュバン(Langevin)関数である. - "Gent"材料モデルはエネルギー密度関数
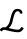 に基づいている.ただし,
に基づいている.ただし,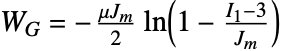 は最初の歪み不変量,
は最初の歪み不変量,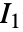 はせん断弾性率,
はせん断弾性率,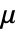 は極限値である.
は極限値である. - "NeoHookean"材料モデルはエネルギー密度関数
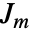 に基づいている.ただし,
に基づいている.ただし,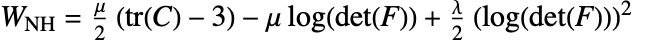 は第1ラメ(Lamé)定数,
は第1ラメ(Lamé)定数,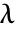 は第2定数,
は第2定数,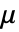 は右コーシー(Cauchy)・グリーン(Green)テンソル,
は右コーシー(Cauchy)・グリーン(Green)テンソル,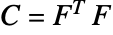 は変形勾配である.
は変形勾配である. - 圧縮可能な"StVenantKirchhoff"材料モデルはエネルギー密度関数
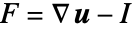 に基づいている.ただし,
に基づいている.ただし,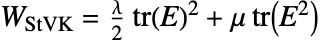 は第1ラメ定数,
は第1ラメ定数,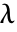 は第2定数,
は第2定数,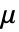 はグリーン・ラグランジュ歪みである.
はグリーン・ラグランジュ歪みである. - "MooneyRivlin"材料モデルはエネルギー密度関数
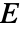 に基づいている.ただし,
に基づいている.ただし,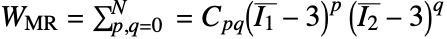 は材料係数,
は材料係数,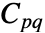 と
と 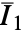 は第1および第2の等重歪み不変量である.
は第1および第2の等重歪み不変量である. - "Yeoh"材料モデルはエネルギー密度関数
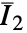 に基づいている.ただし,
に基づいている.ただし,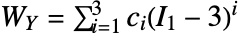 はモデル定数で
はモデル定数で 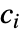 は最初の不変量である.
は最初の不変量である. - 可能な場合はモデルの"Compressibility"が"NearlyIncompressibile"または"Compressibile"として指定できる.
- ほぼ圧縮不可能性は,歪みエネルギー密度関数
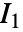 に加えられた静水圧
に加えられた静水圧 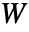 として実装されている.
として実装されている.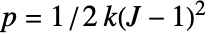 は材料の体積弾性率である.
は材料の体積弾性率である. - すべての超弾性モデルで,平面歪みと平面応力のモデル形式が使用できる.
- 超弾性材料モデルはどれも標準の強化材料モデルを利用して繊維強化材料などの横方向等方性材料がモデル化できる.
- SolidMechanicsPDEComponentは"SIBase"単位を使う.幾何学配置は偏微分方程式と同じ単位でなければならない.
- SolidMechanicsPDEComponentが…,keypi…,pivi,…]として連想 pars で指定されているパラメータ
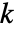 に依存するなら,パラメータ
に依存するなら,パラメータ 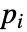 は
は 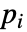 で置き換えられる.
で置き換えられる.

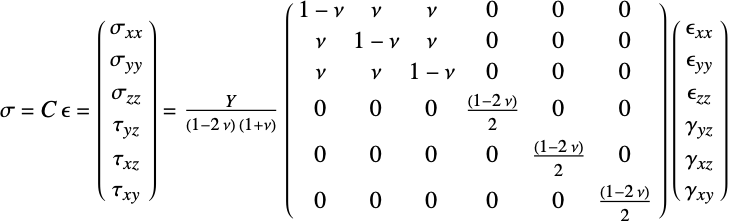
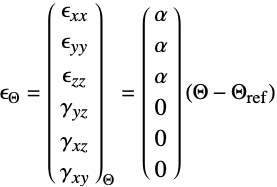
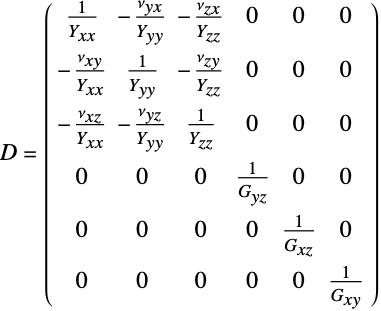
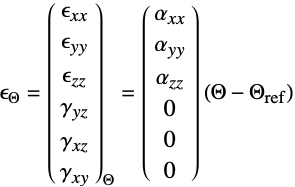
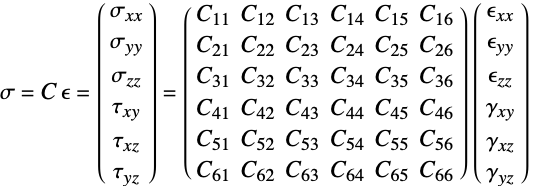
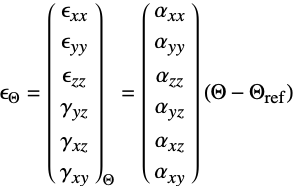
例題
すべて開くすべて閉じるスコープ (22)
定常解析 (2)
定常平面応力解析 (4)
左端が固定されて右端が強制的に動かされる長方形鋼板の変位を計算する.領域,変数,パラメータを設定する:
平面応力のケースを拡張モデルとして計算する.これによって面外応力が計算でき,平面外応力が0であることが検証される.左端が固定され右側が強制的に変位された長方形の鋼板がある.領域,変数,パラメータを設定する.変数には3つすべての方向が含まれる:
変位のリストに3つの出力変数が含まれるようになった.主変数についての移動を可視化する:
左端が固定され右端に圧力が加えられた長方形鋼板の変位を計算する.領域,変数,パラメータを設定する:
定常平面歪み解析 (3)
時間依存解析 (3)
固有モード解析 (2)
超弾性材料モデル (2)
繊維強化材料モデル (1)
マルチマテリアルモデル (1)
アプリケーション (1)
地質工学 (1)
地質工学のアプリケーションで土をモデリングする際は,土の深さでヤング率を変えることができる.この例は,位置に依存するヤング率について調べる.縦横がそれぞれ100メートルの長方形の固体スラブを使う:
次に,変数とパラメータを設定する.この時点でヤング率の記号 ![]() を使う:
を使う:
左側と右側には ![]() 方向の制約がある.土は
方向の制約がある.土は ![]() 方向には自由に動くことができる.底では,土は
方向には自由に動くことができる.底では,土は ![]() 方向に動くことはできるが
方向に動くことはできるが ![]() 方向には動けない.以下で,土が動かない「より固い」地面に立っている場合をモデル化する:
方向には動けない.以下で,土が動かない「より固い」地面に立っている場合をモデル化する:
ヤング率 ![]() をbaseYoungModulusに設定し,細分化されたメッシュ上で偏微分方程式を解く:
をbaseYoungModulusに設定し,細分化されたメッシュ上で偏微分方程式を解く:
テキスト
Wolfram Research (2021), SolidMechanicsPDEComponent, Wolfram言語関数, https://reference.wolfram.com/language/ref/SolidMechanicsPDEComponent.html (2025年に更新).
CMS
Wolfram Language. 2021. "SolidMechanicsPDEComponent." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2025. https://reference.wolfram.com/language/ref/SolidMechanicsPDEComponent.html.
APA
Wolfram Language. (2021). SolidMechanicsPDEComponent. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/SolidMechanicsPDEComponent.html