StratonovichProcess
StratonovichProcess[{a,b},x,t]
表示一个 Stratonovich 过程 ![]() ,
,![]() .
.
StratonovichProcess[{a,b,c},x,t]
表示一个 Stratonovich 过程 ![]() ,其中
,其中 ![]() .
.
StratonovichProcess[…,…,{x,x0},{t,t0}]
表示一个 Stratonovich 过程,其初始条件为 ![]() .
.
StratonovichProcess[…,…,…,Σ]
使用一个维纳过程 ![]() ,其协方差为 Σ.
,其协方差为 Σ.
StratonovichProcess[proc]
将 proc 尽可能转换成一个标准 Stratonovich 过程.
StratonovichProcess[sdeqns,expr,x,t,wdproc]
表示一个 Stratonovich 过程,由一个随机微分方程 sdeqns 所指定,输出表达式为 expr,状态为 x,时间为 t,被遵循过程 dproc 的 w 所驱动.
更多信息和选项



- StratonovichProcess 又被称为 Stratonovich 扩散或随机微分方程 (SDE).
- StratonovichProcess 是一个连续时间和连续状态的随机过程.
- 如果漂移 a 是一个
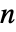 -维向量,扩散 b 是一个
-维向量,扩散 b 是一个  ×
×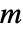 -维矩阵,则这个过程
-维矩阵,则这个过程 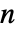 -维,而且被一个
-维,而且被一个 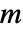 -维 WienerProcess 所驱动.
-维 WienerProcess 所驱动. - 系数 a 和 b 常用规范包括:
-
a 标量,b 标量 
a 标量,b 向量 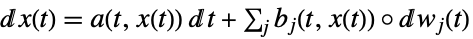
a 向量,b 向量 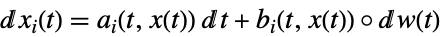
a 向量,b 矩阵 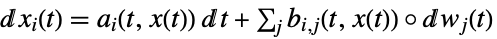
- 随机微分方程
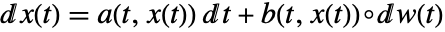 有时候会被写成积分方程
有时候会被写成积分方程 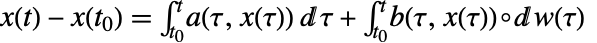 .
. - 默认的初始时间 t0 被认为是零,并且默认初始状态 x0 是零.
- 默认的协方差 Σ 是单位矩阵.
- 一个标准 Stratonovich 过程有输出
 ,由一个微分状态
,由一个微分状态 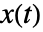 的子集组成.
的子集组成. - 可以被转换成标准 StratonovichProcess 形式的过程 proc 包括 OrnsteinUhlenbeckProcess,GeometricBrownianMotionProcess,ItoProcess 以及 StratonovichProcess.
- sdeqns 中的随机微分方程可以为
 的形式,其中
的形式,其中 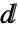 是 \[DifferentialD],可以用
是 \[DifferentialD],可以用  dd
dd 输入. 微分s
输入. 微分s 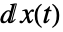 和
和 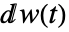 被认为是 Stratonovich 微分.
被认为是 Stratonovich 微分. - 输出表达式 expr 可以为任何包含 x[t] 和 t 的表达式.
- 驱动过程 dproc 可以是能转换成标准 Stratonovich 过程的任何过程.
- 与 StratonovichProcess 过程相关的属性包括:
-
"Drift" 漂移项 "Diffusion" 扩散矩阵 "Output" 输出状态 "TimeVariable" 时间变量 "TimeOrigin" 时间变量起点 "StateVariables" 状态变量 "InitialState" 初始状态值 "KolmogorovForwardEquation" Kolmogorov 正向方程(Fokker-Planck 方程) "KolmogorovBackwardEquation" Kolmogorov 后向方程 "Derivative" Stratonovich 导数 - RandomFunction 中针对 StratonovichProcess 的 Method 设置包括: »
-
"EulerMaruyama" 欧拉-丸山(1/2 阶,默认) "KloedenPlatenSchurz" Kloeden–Platen–Schurz(3/2 阶) "Milstein" 米尔斯坦(1 阶) "StochasticRungeKutta" 3‐级龙格- 库塔法(1 阶) "StochasticRungeKuttaScalarNoise" 标量噪音的 3‐级龙格- 库塔法(3/2阶) - StratonovichProcess 可以和函数 RandomFunction, CovarianceFunction,PDF 和 Expectation 等一起使用.
范例
打开所有单元关闭所有单元范围 (16)
基本用途 (10)
用不同的方法模拟 StratonovichProcess 路径:
用 RandomFunction 中的选项指定模拟的方法:
过程属性提取 (1)
特殊 Stratonovich 过程 (5)
对应于 WienerProcess 的一个 Stratonovich 过程:
对应于 GeometricBrownianMotionProcess 的一个 Stratonovich 过程:
对应于 BrownianBridgeProcess 的一个 Stratonovich 过程:
对应于 OrnsteinUhlenbeckProcess 的一个 Stratonovich 过程:
对应于 CoxIngersollRossProcess 的一个 Stratonovich 过程:
应用 (3)
定义一个向量过程,它对应于迭代的 Stratonovich 积分 ![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() :
:
自由粒子在热涨落作用下的动力学可以用 Langevin 运动方程来模拟,![]() ,其中
,其中 ![]() 是标准 WienerProcess,
是标准 WienerProcess,![]() 是热噪声的强度. 此处假设
是热噪声的强度. 此处假设 ![]() 只依赖于
只依赖于 ![]() ,着重考虑速度方程. 运动方程的积分有两种常用的方法:Ito 公式和 Stratonovich 公式:
,着重考虑速度方程. 运动方程的积分有两种常用的方法:Ito 公式和 Stratonovich 公式:
当 ![]() 是常数时,两个公式是一样的,当
是常数时,两个公式是一样的,当 ![]() 时趋向于相同的平稳分布:
时趋向于相同的平稳分布:
如果 ![]() 依赖于速度,那么,由于 WienerProcess 的特性,
依赖于速度,那么,由于 WienerProcess 的特性,![]() 具有非零二次方差,并且两个公式导致不同的结果. 将 Ito 公式转换为等效的 Stratonovich 公式:
具有非零二次方差,并且两个公式导致不同的结果. 将 Ito 公式转换为等效的 Stratonovich 公式:
Stratonovich 公式下的漂移与 Ito 公式下的漂移不同:
创建一个 OrnsteinUhlenbeckProcess,并用 StratonovichProcess 来表示:
![]() 条件下用数值法求解方程,提供
条件下用数值法求解方程,提供 ![]() 处的局部初始条件和 Dirichlet 边界条件:
处的局部初始条件和 Dirichlet 边界条件:
绘制 ![]() 时 Kolmogorov 正向方程的解,将其与解析密度函数进行比较:
时 Kolmogorov 正向方程的解,将其与解析密度函数进行比较:
用 Animate 可视化解:
属性和关系 (1)
将 ItoProcess 转换至 StratonovichProcess:
可能存在的问题 (2)
StratonovichProcess 不支持随机初始条件,所有无法被表示:
驱动过程的起始时间需和 StratonovichProcess 匹配:
文本
Wolfram Research (2012),StratonovichProcess,Wolfram 语言函数,https://reference.wolfram.com/language/ref/StratonovichProcess.html.
CMS
Wolfram 语言. 2012. "StratonovichProcess." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/StratonovichProcess.html.
APA
Wolfram 语言. (2012). StratonovichProcess. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/StratonovichProcess.html 年