ToeplitzMatrix
给出 n×n 阶托普利兹矩阵,它的首行首列为连续整数.
ToeplitzMatrix[{c1,c2,…,cn}]
给出托普利兹矩阵,其第一列由 c1、c2、… 等项组成.
ToeplitzMatrix[{c1,c2,…,cm},{r1,r2,…, rn}]
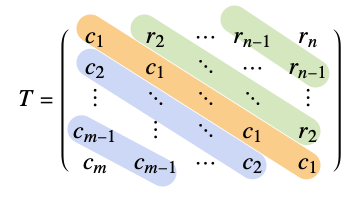
给出托普利兹矩阵,其第一列为 ci 各项,第一行为 ri 各项.
更多信息和选项


- 托普利兹矩阵通常出现在与逼近理论、信号处理、统计和时间序列相关的应用中.
- 托普利兹矩阵是指每条对角线均为常数的矩阵. 当
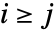 时,托普利兹矩阵
时,托普利兹矩阵 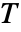 的各项由
的各项由 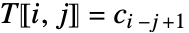 给出,否则由
给出,否则由 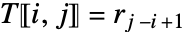 给出.
给出. - 元素 r1 必须等于元素 c1. »
- ToeplitzMatrix[…,TargetStructure->struct] 以 struct 指定的格式返回托普利兹矩阵. 可能的设置包括:
-
Automatic 自动选择返回的表示 "Dense" 将矩阵表示为稠密矩阵 "Structured" 将矩阵表示为结构化数组 "Symmetric" 将矩阵表示为对称矩阵 - 对于 ToeplitzMatrix[…,TargetStructureAutomatic],如果矩阵项的数量小于预设阈值,则返回密集矩阵,否则返回结构化数组.
- 对于结构化的 ToeplitzMatrix sa,以下属性 "prop" 可以作为 sa["prop"] 访问:
-
"ColumnVector" 第一列项组成的向量 "RowVector" 第一行项组成的向量 "Properties" 支持的属性列表 "Structure" 结构化数组的类型 "StructuredData" 结构化数组存储的内部数据 "StructuredAlgorithms" 具有结构化数组特殊方法的函数列表 "Summary" 摘要信息,表示为 Dataset - Normal[ToeplitzMatrix[…]] 将结构化托普利兹矩阵转换为普通矩阵.
范例
打开所有单元关闭所有单元范围 (9)
ToeplitzMatrix 对象包括提供有关数组信息的属性:
"ColumnVector" 属性给出托普利兹矩阵的第一列:
"StructuredAlgorithms" 属性列出具有结构化算法的函数:
在适当的时候,结构算法返回另一个 ToeplitzMatrix 对象:
其转置也是 ToeplitzMatrix:
选项 (2)
TargetStructure (2)
通过设置 TargetStructureAutomatic,返回小尺寸的密集矩阵:
应用 (10)
生成的对角矩阵的对角元素与傅立叶矩阵和起始向量的乘积相同,直至一个常数缩放因子:
托普利兹矩阵的逆矩阵可以仅根据逆矩阵的第一列和最后一列来确定. 使用 LinearSolve 计算逆矩阵的第一列:
托普利兹矩阵的逆的 Gohberg–Semencul 公式使用第一列和最后一列来组成完整的逆矩阵:
对于前几种情况,用第二类切比雪夫多项式验证特征多项式的表达式:
三对角托普利兹矩阵可以通过 1 类离散正弦变换矩阵的对角重新缩放来对角化:
将 Kac–Murdock–Szegő (KMS) 矩阵定义为 ToeplitzMatrix:
KMS 矩阵是一阶自回归过程(即 AR(1) 过程)的相关矩阵:
将 Parter 矩阵定义为 ToeplitzMatrix:
长球波矩阵(prolate matrix)是一个对称正定托普利兹矩阵,出现在多锥功率谱密度估计中:
2-范数条件数是由于对称性而导致的最大特征值与最小特征值之比:
2012 年 5 月至 2012 年 9 月欧元兑美元每日汇率:
通过求解 Yule-Walker 方程,将 3 阶自回归过程 (ARProcess) 拟合到汇率:
相同的结果可以从 EstimatedProcess 得到:
从幂级数系数可以得到函数 ![]() 关于点 x=x0 的
关于点 x=x0 的 ![]() 阶帕德(Padé)近似. 定义函数、分子和分母度数以及展开点:
阶帕德(Padé)近似. 定义函数、分子和分母度数以及展开点:
分母的系数可以通过求解由幂级数系数构造的托普利兹系统来获得:
分子的系数可以通过将分母系数向量与由幂级数系数构造的托普利兹矩阵相乘来获得:
与 PadeApproximant 的结果比较:
验证牛顿-吉拉德公式 [MathWorld] ,这些公式涉及幂和与初等对称多项式:
将 Ching 矩阵定义为 ToeplitzMatrix:
属性和关系 (5)
具有零填充的循环 ListConvolve 等效于与下三角托普利兹矩阵相乘:
具有零填充的循环 ListCorrelate 等价于与上三角托普利兹矩阵相乘:
如果 c1 是实数,则 ToeplitzMatrix[{c1,c2,…}] 为埃尔米特矩阵:
ToeplitzMatrix 和 HankelMatrix 通过与交换矩阵(反向单位矩阵)相乘来关联:
文本
Wolfram Research (2007),ToeplitzMatrix,Wolfram 语言函数,https://reference.wolfram.com/language/ref/ToeplitzMatrix.html (更新于 2024 年).
CMS
Wolfram 语言. 2007. "ToeplitzMatrix." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2024. https://reference.wolfram.com/language/ref/ToeplitzMatrix.html.
APA
Wolfram 语言. (2007). ToeplitzMatrix. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/ToeplitzMatrix.html 年