

TreeFold
Details

- TreeFold constructs an expression from a Tree object, folding its subtrees from the bottom up using a binary operation f:
- TreeFold is useful for accumulating or reducing the data or subtrees of a tree to a single value.
- TreeFold folds subtrees in a depth-first order, folding children before folding parents: »
- In TreeFold[f,tree,h], h[tree] is used as the first argument of f rather than TreeData[tree]. »
- TreeFold[{…,f-1},tree,h] gives f-1[h[tree]] if tree is a leaf. »
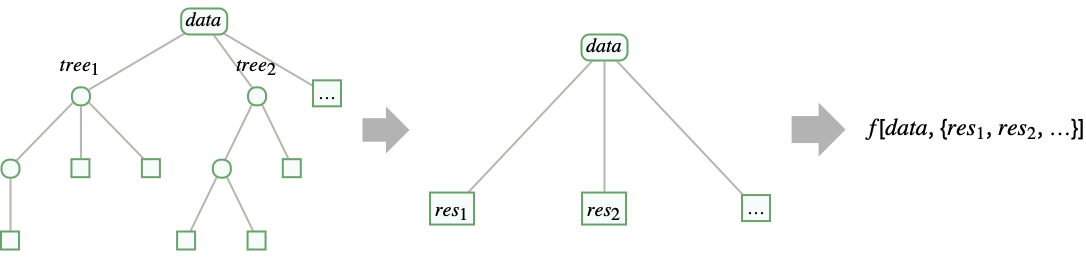
- TreeFold[f,Tree[data,<|key1tree1,key2tree2,…|>]] gives f[data,<|key1res1,key2res2,…|>], where resi is the result of TreeFold[f,treei]. »
- TreeFold[f][tree] is equivalent to TreeFold[f,tree]. »
- TreeFold[f][tree,h] is equivalent to TreeFold[f,tree,h]. »

Examples
open all close allBasic Examples (4)
Scope (9)
Applications (11)
Convert a tree of solid regions and operations into a CSGRegion:
Get a nested list of the data in the leaves of a tree:
Construct a tree from the atoms of an expression:
Convert this tree to nested lists:
Total the data in the leaves of a tree:
Create a tree of terms in a linear recurrence:
Compute the terms of the linear recurrence:
Convert a tree to a TextElement:
Compute the minimum level of leaves in a tree using TreeFold with this function:
Get a list of US cities with populations over 100,000:
Construct a graph giving the hierarchical clustering of the cities according to their geodetic positions:
Convert the clustering hierarchy from a Graph object to a Tree object:
For each leaf, obtain the geodetic position of a city from its index in the hierarchical clustering graph:
For each subtree representing a cluster, give the tree containing the spatial median of its children:
Obtain a tree of geodetic positions by using the position of a city for each leaf and the spatial median of the positions for each cluster:
Show the edges in this tree of geodetic positions on a map of the United States:
Create an association giving the dates of birth:
Define a function that compares two people, giving the person who was younger when they had their first child, together with that child and their age when that child was born:
Define a function that compares two siblings, giving the older sibling together with their date of birth, in addition to the youngest first-time parent among their descendants:
Define a function that gives the youngest first-time parent among a person's descendants, given the results for their children:
Find the youngest first-time parent in the tree, together with their first child and their age when the child was born:
Properties & Relations (14)
Fold gives the result of successively applying a binary operator f to the elements of a list:
TreeFold gives the result of successively applying a binary operator f to the data of a tree:
TreeFold applies the operator f to the list of results for each child:
TreeFold[f,Tree[data,None]] gives data:
TreeFold[{f,f-1},Tree[data,None]] applies the operator f-1 to data instead:
TreeFold[f,Tree[data,{…}]] gives f[data,{…}]:
This is true even if the tree has no children:
TreeFold[f,tree,h] gives the result of applying f to both h[tree] and the list of results TreeFold[f,treei,h] for the children treei:
TreeFold[f,tree] is equivalent to TreeFold[{f,Identity},tree]:
TreeFold[{Tree,Tree[#,None]&},tree] is equivalent to tree:
TreeFold applies a function to the data and results for the children:
TreeMap can compute the same result:
The new data of the root is the result of TreeFold:
Construct a tree from the heads in an expression:
Use TreeFold to insert a parent node above each subtree:
This corresponds to mapping on the arguments in an expression:
Map maps on the arguments in an expression by default:
Construct a tree from the atoms in an expression:
Use TreeFold to insert a sibling node before each subtree:
This corresponds to mapping on the subexpressions in an expression:
Map maps on the subexpressions in an expression with HeadsTrue:
TreeFold[{f,f-1},tree] is equivalent to TreeFold[f,TreeMap[f-1,tree,{-1}]]:
First map the operator f-1 on the leaves of the tree:
Then fold the tree using the operator f for internal subtrees:
TreeFold can be used to compute the depth of a tree:
TreeFold can be used to compute the size of a tree:
TreeFold can be used to convert a tree to nested rules:
TreeFold can be used to create an expression from the leaves of a tree:
Neat Examples (2)
Related Guides
Text
Wolfram Research (2021), TreeFold, Wolfram Language function, https://reference.wolfram.com/language/ref/TreeFold.html (updated 2022).
CMS
Wolfram Language. 2021. "TreeFold." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2022. https://reference.wolfram.com/language/ref/TreeFold.html.
APA
Wolfram Language. (2021). TreeFold. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/TreeFold.html
BibTeX
@misc{reference.wolfram_2025_treefold, author="Wolfram Research", title="{TreeFold}", year="2022", howpublished="\url{https://reference.wolfram.com/language/ref/TreeFold.html}", note=[Accessed: 05-January-2026]}
BibLaTeX
@online{reference.wolfram_2025_treefold, organization={Wolfram Research}, title={TreeFold}, year={2022}, url={https://reference.wolfram.com/language/ref/TreeFold.html}, note=[Accessed: 05-January-2026]}