WOLFRAM

Wolfram言語 ＆ システムドキュメントセンター

TruncateSum[sexpr,n]

sexpr 内の各Sumの項を切り捨てて最大で n 項になるようにする．

TruncateSum[sexpr,{m,n,…}]

反復指定{m,n,…}を使って sexpr 内の各多重Sumの項を切り捨てる．

詳細とオプション
Details and Options Details and Options
例題  
例  
スコープ  
基本的な用法  
有限和  
無限和  
多重和  
非アクティブな和  
オプション  
WorkingPrecision  
ActivateResult  
アプリケーション  
微分方程式  
差分方程式  
漸近  
逆ラプラス変換  
特性と関係  
考えられる問題  
関連項目
関連するガイド
履歴
引用書式

TruncateSum

TruncateSum[sexpr,n]

sexpr 内の各Sumの項を切り捨てて最大で n 項になるようにする．

TruncateSum[sexpr,{m,n,…}]

反復指定{m,n,…}を使って sexpr 内の各多重Sumの項を切り捨てる．

詳細とオプション

  • TruncateSumは，通常，近似評価が簡単になるように，無限和を含む記号解を切り捨てて有限和にするために使われる．
  • 総和の式 sexpr は，未評価およびInactiveな総和の任意の組み合せでよい．
  • TruncateSumは，以下に従って大きい正または負の総和の極限を切り捨てる．
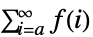
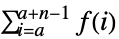
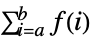
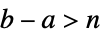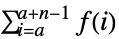
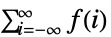
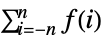
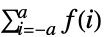
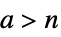  • のとき
    のとき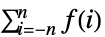
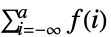
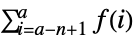
  • 次は，使用可能なオプションである．
  • ActivateResult True結果をActivateするかどうか
    WorkingPrecision Automatic内部計算の精度

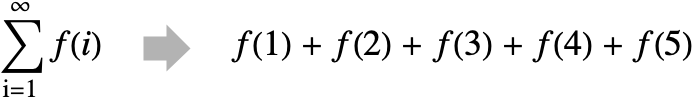
例題

すべて開く すべて閉じる

例  (2)

無限和を最初の12項を残して切り捨てる：

Wolfram Language code: TruncateSum[Sum[f[i], {i, 1, ∞}], 12]

非アクティブな和を切り捨てる：

Wolfram Language code: expr = Inactive[Sum][1 / x^i, {i, 1, ∞}]
Wolfram Language code: TruncateSum[expr, 5]

非アクティブな和をアクティブにしないようにする：

Wolfram Language code: TruncateSum[Inactive[Sum][x^(-i), {i, 1, Infinity}], 5, ActivateResult -> False]

結果をアクティブにする：

Wolfram Language code: Activate[%]

スコープ  (13)

基本的な用法  (3)

無限和を最初の10項を残して切り捨てる：

Wolfram Language code: expr = Sum[Sin[x^i], {i, 1, Infinity}]
Wolfram Language code: TruncateSum[expr, 10]

無限和を切り捨てて記号による上限がある和にする：

Wolfram Language code: expr = Inactive[Sum][Exp[-Sin[x]], {x, 1, Infinity}]
Wolfram Language code: TruncateSum[expr, m]

未評価の和については，TruncateSumは切捨て和を直接評価する：

Wolfram Language code: expr = Sum[Cos[i], {i, 3, Infinity}]
Wolfram Language code: TruncateSum[expr, 7]

有限和  (3)

有限和を切り捨てる：

Wolfram Language code: TruncateSum[Inactive[Sum][Tanh[x]^i, {i, 1, 1000}], 5]

記号による上限がある和を切り捨てる：

Wolfram Language code: expr = Sum[Sin[x^i], {i, 1, n}]
Wolfram Language code: TruncateSum[expr, 10]

記号的な上限と下限がある和を切り捨てる：

Wolfram Language code: expr = Inactive[Sum][(-x)^n, {n, -100, 100}];
Wolfram Language code: TruncateSum[expr, 10, ActivateResult -> False]

無限和  (4)

無限和を切り捨てる：

Wolfram Language code: expr = Sum[1 / n, {n, 1, Infinity}]
Wolfram Language code: TruncateSum[expr, 14]

二重無限和を切り捨てる：

Wolfram Language code: TruncateSum[Inactive[Sum][Sin[x^i], {i, -Infinity, Infinity}], 10, ActivateResult -> False]
Wolfram Language code: Activate[%]

–∞ を下限とする和を切り捨てる：

Wolfram Language code: TruncateSum[Inactive[Sum][Cos[n + x], {n, -Infinity, 0}], 5]

無限和の係数を持つ多項式を切り捨てる：

Wolfram Language code: pol = x^2 Inactive[Sum][Sin[i], {i, 1, Infinity}] + x Inactive[Sum][Cos[j], {j, 1, Infinity}] + Inactive[Sum][E^(-k), {k, 1, Infinity}];
Wolfram Language code: N[TruncateSum[pol, 4]]

多重和  (2)

二重無限和を切り捨てる：

Wolfram Language code: expr = Inactive[Sum][Sin[i*j], {i, 1, Infinity}, {j, 1, Infinity}];
Wolfram Language code: TruncateSum[expr, 5]

各総和について合計項数の最大数を指定する：

Wolfram Language code: TruncateSum[expr, {3, 4}]

最初の和だけを切り捨てる：

Wolfram Language code: TruncateSum[expr, {4, All}]

2番目の和だけを切り捨てる：

Wolfram Language code: TruncateSum[expr, {All, 4}]

二重和を切り捨てる：

Wolfram Language code: dsum = Underoverscript[∑, i = 1, ∞]Underoverscript[∑, j = 1, 10](i^2 + j^3);
Wolfram Language code: TruncateSum[dsum, 5]

個々の項数の最大数を指定する：

Wolfram Language code: TruncateSum[dsum, {3, 4}]

非アクティブな和  (1)

TruncateSumは，非アクティブな和については切捨て和を評価しようとする：

Wolfram Language code: expr = Inactive[Sum][i^2, {i, 1, Infinity}]
Wolfram Language code: TruncateSum[expr, n]

ActivateResultFalseを使って非アクティブな和をアクティブにしないようにする：

Wolfram Language code: TruncateSum[expr, n, ActivateResult -> False]

結果をあアクティブにする：

Wolfram Language code: Activate[%]

オプション  (2)

WorkingPrecision  (1)

二重和を切り捨てる：

Wolfram Language code: sum = Sum[x Cos[x y], {x, 1, Infinity}, {y, 1, 10}]
Wolfram Language code: TruncateSum[sum, 10]//N

20桁精度計算で和を切り捨てる：

Wolfram Language code: TruncateSum[sum, 10, WorkingPrecision -> 20]

ActivateResult  (1)

Inactive和を切り捨てる：

Wolfram Language code: expr = Inactive[Sum][i^2, {i, 1, Infinity}]
Wolfram Language code: TruncateSum[expr, n]

ActivateResult→Falseを使って切捨て和がアクティブにならないようにする：

Wolfram Language code: TruncateSum[expr, n, ActivateResult -> False]

アプリケーション  (10)

微分方程式  (4)

有限区間の波動方程式についてのディリクレ(Dirichlet)問題を解く：

Wolfram Language code: weqn = D[u[x, t], {t, 2}] == D[u[x, t], {x, 2}]; ic = {u[x, 0] == x ^ 2(Pi - x), Derivative[0, 1][u][x, 0] == 0}; bc = {u[0, t] == 0, u[Pi, t] == 0};

解は無限三角級数である：

Wolfram Language code: sol = DSolveValue[{weqn, ic, bc}, u[x, t], {x, t}]

Inactive和から最初の3項を抽出する：

Wolfram Language code: asol = TruncateSum[sol, 3]
Wolfram Language code: Plot3D[asol, {x, 0, Pi}, {t, 0, 4Pi}, ColorFunction -> Hue]

矩形内の波動方程式についてのディリクレ問題を解く：

Wolfram Language code: weqn = D[u[x, y, t], {t, 2}] == Laplacian[u[x, y, t], {x, y}];
Wolfram Language code: ic = {u[x, y, 0] == (1 / 10)(x - x ^ 2)(2y - y ^ 2), Derivative[0, 0, 1][u][x, y, 0] == 0};
Wolfram Language code: bc = {u[x, 0, t] == 0, u[0, y, t] == 0, u[1, y, t] == 0, u[x, 2, t] == 0};

解は二重無限三角級数である：

Wolfram Language code: (sol = FullSimplify[DSolveValue[{weqn, ic, bc}, u[x, y, t], {x, y, t}], K[1]∈Integers && K[3]∈Integers && K[1] ≥ 1 && K[3] ≥ 1])//TraditionalForm

Inactive和から数項抽出する：

Wolfram Language code: h[x_, y_, t_] = TruncateSum[sol, 5]
Wolfram Language code: Animate[Plot3D[h[x, y, t], {x, 0, 1}, {y, 0, 2}, Ticks -> False, PlotRange -> {-1 / 36, 1 / 36}, MeshStyle -> Red, PerformanceGoal -> "Quality"], {t, 0, 8}, SaveDefinitions -> True, DefaultDuration -> 12, AnimationRepetitions -> 1]

有限区間の熱伝導方程式についてのディリクレ問題を解く：

Wolfram Language code: heqn = D[u[x, t], t] == D[u[x, t], {x, 2}]; ic = u[x, 0] == x(3 - x) ^ 2; bc = {u[0, t] == 0, u[3, t] == 0};

解はフーリエ正弦級数である：

Wolfram Language code: sol = DSolveValue[{heqn, ic, bc }, u[x, t], {x, t}]

Inactive和を切り捨てる：

Wolfram Language code: asol = TruncateSum[sol, 3]
Wolfram Language code: Plot3D[asol//Evaluate, {x, 0, 3}, {t, 0, 3 / 2}, Exclusions -> None, PlotRange -> All]

ディリクレ境界条件があるシュレディンガー(Schrödinger)方程式についての初期値問題を解く：

Wolfram Language code: eqn = I D[ψ[x, t], t] == -2 D[ψ[x, t], {x, 2}]; f[x_] := -350 + 155 x - 22 x^2 + x^3 sol = DSolveValue[{eqn, ψ[5, t] == 0, ψ[10, t] == 0, ψ[x, 2] == f[x]}, ψ, {x, t}]

解の部分和集合を定義する：

Wolfram Language code: u[k_Integer] = TruncateSum[sol, k]

ukは，各 k について微分方程式を満足する：

Wolfram Language code: Table[eqn /. ψ -> u[k], {k, 4}]//Simplify

境界条件も満足される：

Wolfram Language code: Table[{u[k][5, t] == 0, u[k][10, t] == 0}, {k, 4}]

初期条件は u∞についてしか満足されないが，t==2で急速に収束する：

Wolfram Language code: Grid@Partition[Table[Plot[{u[k][x, 2], f[x]}, {x, 5, 10}, ImageSize -> 200], {k, 4}], 2]

差分方程式  (1)

差分方程式を解く：

Wolfram Language code: sol = RSolveValue[y[k + 1] - y[k] == Sin[k^2], y[k], k]

についての解を抽出する：

Wolfram Language code: TruncateSum[sol, 10]

漸近  (3)

0の周りののベキ級数展開を計算する：

Wolfram Language code: pse = Asymptotic[Sin[x], {x, 0, Infinity}]

級数の最初の7つの非零の項を取得する：

Wolfram Language code: TruncateSum[pse, 7]

1の周りの のベキ級数展開を計算する：

Wolfram Language code: Asymptotic[E ^ x, {x, 1, Infinity}]

級数の最初の5項を取得する：

Wolfram Language code: TruncateSum[%, 5]

一連のHypergeometric1F1関数を切り捨てる：

Wolfram Language code: h1f1[a_, b_, z_] = Inactive[Sum][(Pochhammer[a, i]z^i/Pochhammer[b, i]i!), {i, 0, Infinity}]
Wolfram Language code: f[a_, b_, z_, n_] = TruncateSum[h1f1[a, b, z], n + 1]

結果を組込みのHypergeometric1F1関数と比較する：

Wolfram Language code: Table[(Hypergeometric1F1[a, b, z] - f[a, b, z, n]) /. {a -> 1.1, b -> 1.2, z -> 2.3}, {n, 5, 20, 5}]
Wolfram Language code: Plot[{Hypergeometric1F1[-1.1, 2, z], f[-1.1, 2, z, 5], f[-1.1, 2, z, 10], f[-1.1, 2, z, 15]}, {z, 0, 17}, PlotLegends -> {"Exact", "n=5", "n=10", "n=15"}]

逆ラプラス変換  (2)

関数の逆ラプラス変換を計算する：

Wolfram Language code: ilt = InverseLaplaceTransform[1 / (s Sinh[3 s] Sinh[5 s]), s, t]

和を切り捨てて結果をプロットする：

Wolfram Language code: Plot[TruncateSum[ilt, 45], {t, 0, 60}]

この関数の逆ラプラス変換は区分関数である：

Wolfram Language code: ilt = InverseLaplaceTransform[((Exp[s] - 1) Sin[π / 5]) / (s (Exp[2 s] - 2 Exp[s] Cos[π / 5] + 1)), s, t]

切り捨てて結果をプロットする：

Wolfram Language code: Plot[TruncateSum[ilt, 6], {t, 0, 15}]

特性と関係  (4)

TruncateSum[expr,n]は，式の各和が最高で n 項になるように切り捨てる：

Wolfram Language code: TruncateSum[Underoverscript[∑, i = 1, ∞]f[i] + Underoverscript[∑, j = 1, ∞]g[j], 4]

TruncateSumは，二重無限和の両方の極限を切り捨てる：

Wolfram Language code: TruncateSum[Underoverscript[∑, i = -∞, ∞]f[i], 4]

TruncateSumは，–∞ から無限の値までの和の下極限だけを切り捨てる：

Wolfram Language code: TruncateSum[Underoverscript[∑, i = -∞, 0]f[i], 4]

TruncateSumは式内のすべての非アクティブな和をアクティブにする：

Wolfram Language code: expr = Inactive[Sum][f[i], {i, 1, 100}]
Wolfram Language code: TruncateSum[expr, 5]

ActivateResult Falseを使ってアクティブにしないようにできる：

Wolfram Language code: TruncateSum[expr, 5, ActivateResult -> False]

考えられる問題  (1)

切捨て和の項数は整数であると仮定される：

Wolfram Language code: TruncateSum[Inactive[Sum][x^(-i), {i, 1, Infinity}], 10.5]
Wolfram Language code: TruncateSum[Inactive[Sum][x^(-i), {i, 1, Infinity}], 10]
Wolfram Research (2024), TruncateSum, Wolfram言語関数， https://reference.wolfram.com/language/ref/TruncateSum.html.

テキスト

Wolfram Research (2024), TruncateSum, Wolfram言語関数， https://reference.wolfram.com/language/ref/TruncateSum.html.

CMS

Wolfram Language. 2024. "TruncateSum." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/TruncateSum.html.

APA

Wolfram Language. (2024). TruncateSum. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/TruncateSum.html

BibTeX

@misc{reference.wolfram_2026_truncatesum, author="Wolfram Research", title="{TruncateSum}", year="2024", howpublished="\url{https://reference.wolfram.com/language/ref/TruncateSum.html}", note=[Accessed: 02-November-2026]}

BibLaTeX

@online{reference.wolfram_2026_truncatesum, organization={Wolfram Research}, title={TruncateSum}, year={2024}, url={https://reference.wolfram.com/language/ref/TruncateSum.html}, note=[Accessed: 02-November-2026]}