"Multinormal" (機械学習メソッド)

詳細とサブオプション

  • "Multinormal"は数値空間の確率密度を，MultinormalDistributionにおけるように多変量正規分布を使ってモデル化する．
  • ベクトル の確率密度は に比例する．ただし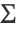， と 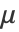は既習パラメータである．n が入力数値ベクトルのサイズのとき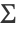， は共分散と呼ばれる n×n 対称正定値行列で 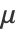はサイズ n のベクトルである．
  • 次は，使用可能なオプションである．
  • "CovarianceType" "Full"共分散行列 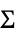についての制約タイプ
    "IntrinsicDimension" Automatic仮定するデータの事実上の次元
  • 次は，"CovarianceType"の可能な設定である．
  • "Diagonal"対角要素のみが既習（他は0に設定）
    "Full"n×n 要素のすべてが既習
    "Spherical"対角要素のみが既習で等しいものとして設定される
  • 次は，"IntrinsicDimension"の可能な設定である．
  • Automaticいくつかの可能な次元を試す
    "Heuristic"データに基づくヒューリスティックを使う
    k指定された次元を使う
  • "CovarianceType""Full"で"IntrinsicDimension"k のとき（ただし，k<n）は，データに対して線形次元削減が行われる． （「信号」部分と解釈される）削減された空間内でのデータのモデル化には完全な k×k 共分散行列が使われ，（「ノイズ」部分と解釈される）残りの n-k 次元のモデル化には球面共分散行列が使われる．
  • "IntrinsicDimension"の値は，"CovarianceType""Diagonal"mまたは"CovarianceType""Spherical"のときは無視される．
  • Information[LearnedDistribution[…],"MethodOption"]を使って，自動システムで選ばれたオプションの値を抽出することができる．
  • LearnDistribution[…,FeatureExtractor"Minimal"]を使ってほとんどの前処理を削除してメソッドに直接アクセスすることができる．

例題

すべて開くすべて閉じる

例  (3)

"Multinormal"分布を数値データ集合で訓練する：

分布のInformationを見る：

オプションの情報を得る：

オプションの値を直接得る：

新たな例の確率密度を計算する：

確率密度関数を訓練データとともにプロットする：

新たなサンプルを生成し，可視化する：

"Multinormal"分布を二次元データ集合で訓練する：

確率密度関数を訓練データとともにプロットする：

SynthesizeMissingValuesを使い，既習の分布を使って欠落値を転嫁する：

"Multinormal"分布を名義的データ集合で訓練する：

必要な前処理のため，確率密度関数の計算は厳密ではない：

ComputeUncertaintyを使って結果についての不確かさを得る：

MaxIterationsを大きくして推定精度を上げる：

オプション  (2)

"CovarianceType"  (1)

"Multinormal"を"Full"共分散の分布で訓練する：

分布の確率密度関数(PDF)を特定の点で評価する：

共分散のタイプが"Full"，"Diagonal"，"Spherical"の多変量で訓練した後で得た確率密度関数を可視化する：

"IntrinsicDimension"  (1)

"Multinormal"分布を"Full"の共分散と固有次元1で訓練する：

この分布から生成されたサンプルを可視化する：

固有次元3で生成されたサンプルと比較する：