LearnDistribution

LearnDistribution[{example1,example2,…}]

generates a LearnedDistribution[…] that attempts to represent an underlying distribution for the examples given.

Details and Options

  • LearnDistribution can be used on many types of data, including numerical, nominal and images.
  • Each examplei can be a single data element, a list of data elements or an association of data elements. Examples can also be given as a Dataset object.
  • LearnDistribution effectively assumes that each of the examplei is independently drawn from an underlying distribution, which LearnDistribution attempts to infer.
  • LearnDistribution[examples] yields a LearnedDistribution[…] on which the following functions can be used:
  • PDF[dist,…]probability or probability density for data
    RandomVariate[dist]random samples generated from the distribution
    SynthesizeMissingValues[dist,…]fill in missing values according to the distribution
    RarerProbability[dist,…]compute the probability to generate a sample with lower PDF than a given example
  • The following options can be given:
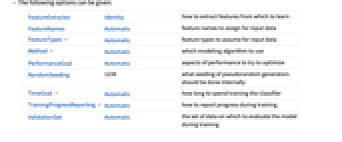
  • FeatureExtractorIdentityhow to extract features from which to learn
    FeatureNamesAutomaticfeature names to assign for input data
    FeatureTypes Automaticfeature types to assume for input data
    Method Automaticwhich modeling algorithm to use
    PerformanceGoalAutomaticaspects of performance to try to optimize
    RandomSeeding1234what seeding of pseudorandom generators should be done internally
    TimeGoal Automatichow long to spend training the classifier
    TrainingProgressReporting Automatichow to report progress during training
    ValidationSetAutomaticthe set of data on which to evaluate the model during training
  • Possible settings for PerformanceGoal include:
  • "DirectTraining"train directly on the full dataset, without model searching
    "Memory"minimize storage requirements of the distribution
    "Quality"maximize the modeling quality of the distribution
    "Speed"maximize speed for PDF queries
    "SamplingSpeed"maximize speed for generating random samples
    "TrainingSpeed"minimize time spent producing the distribution
    Automaticautomatic tradeoff among speed, quality and memory
    {goal1,goal2,…}automatically combine goal1, goal2, etc.
  • Possible settings for Method include:
  • "ContingencyTable"discretize data and store each possible probability
    "DecisionTree"use a decision tree to compute probabilities
    "GaussianMixture"use a mixture of Gaussian (normal) distributions
    "KernelDensityEstimation"use a kernel mixture distribution
    "Multinormal"use a multivariate normal (Gaussian) distribution
  • The following settings for TrainingProgressReporting can be used:
  • "Panel"show a dynamically updating graphical panel
    "Print"periodically report information using Print
    "ProgressIndicator"show a simple ProgressIndicator
    "SimplePanel"dynamically updating panel without learning curves
    Nonedo not report any information
  • Possible settings for RandomSeeding include:
  • Automaticautomatically reseed every time the function is called
    Inheriteduse externally seeded random numbers
    seeduse an explicit integer or strings as a seed
  • Only reversible feature extractors can be given in the option FeatureExtractor.
  • LearnDistribution[…,FeatureExtractor"Minimal"] indicates that the internal preprocessing should be as simple as possible.
  • All images are first conformed using ConformImages.
  • Information[LearnedDistribution[…]] generates an information panel about the distribution and its estimated performances.

Examples

open allclose all

Basic Examples  (3)

Train a distribution on a numeric dataset:

Generate a new example based on the learned distribution:

Compute the PDF of a new example:

Train a distribution on a nominal dataset:

Generate a new example based on the learned distribution:

Compute the probability of the examples "A" and "B":

Train a distribution on a two-dimensional dataset:

Generate a new example based on the learned distribution:

Compute the probability of two examples:

Impute the missing value of an example:

Scope  (3)

Train a distribution on a dataset containing numeric and nominal variables:

Generate a new example based on the learned distribution:

Impute the missing value of an example:

Train a distribution on colors:

Generate 100 new examples based on the learned distribution:

Compute the probability density of some colors:

Train a distribution on dates:

Generate 10 new examples based on the learned distribution:

Compute the probability density of some new dates:

Options  (6)

FeatureTypes  (1)

Specify that the data is nominal:

Without specification, the data is considered numerical:

Method  (2)

Train a "Multinormal" distribution on a numeric dataset:

Plot the PDF along with the training data:

Train a distribution on a two-dimensional dataset with all available methods ("Multinormal", "ContingencyTable", "KernelDensityEstimation", "DecisionTree" and "GaussianMixture"):

Visualize the probability density of these distributions:

TimeGoal  (2)

Learn a distribution while specifying a total training time of 5 seconds:

Load 1000 images of the "MNIST" dataset:

Learn its distribution while specifying a target training time of 3 seconds:

The loss value obtained (cross-entropy) is about -0.43:

Learn its distribution while specifying a target training time of 30 seconds:

The loss value obtained (cross-entropy) is about -0.978:

Compare the learning curves for both trainings:

TrainingProgressReporting  (1)

Load the "UCILetter" dataset:

Show training progress interactively during training:

Show training progress interactively without plots:

Print training progress periodically during training:

Show a simple progress indicator:

Do not report progress:

Applications  (4)

Obtain a dataset of images:

Train a distribution on the images:

Generate 50 new examples based on the learned distribution:

Compare the probability density for an image of the training set, an image of a test set, a sample from the learned distribution, an image of another dataset and a random image:

Obtain the probability to generate a sample with a lower PDF for each of these images:

Load the "FisherIris" dataset:

Train a distribution directly from the Dataset:

Generate a random sample:

Generate several random samples:

Visualize random samples of the variables "PetalLength" and "SepalLength" from the distribution and compare them with the dataset:

Load the Titanic survival dataset:

Train a distribution on the dataset:

Use the distribution and SynthesizeMissingValues to generate complete examples from incomplete ones:

Use the distribution to predict the survival probability of a given passenger:

Train a distribution on a two-dimensional dataset:

Plot the PDF along with the training data:

Use SynthesizeMissingValues to impute missing values using the learned distribution:

Obtain the histogram of possible imputed values:

Wolfram Research (2019), LearnDistribution, Wolfram Language function, https://reference.wolfram.com/language/ref/LearnDistribution.html.

Text

Wolfram Research (2019), LearnDistribution, Wolfram Language function, https://reference.wolfram.com/language/ref/LearnDistribution.html.

CMS

Wolfram Language. 2019. "LearnDistribution." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/LearnDistribution.html.

APA

Wolfram Language. (2019). LearnDistribution. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/LearnDistribution.html

BibTeX

@misc{reference.wolfram_2024_learndistribution, author="Wolfram Research", title="{LearnDistribution}", year="2019", howpublished="\url{https://reference.wolfram.com/language/ref/LearnDistribution.html}", note=[Accessed: 21-December-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_learndistribution, organization={Wolfram Research}, title={LearnDistribution}, year={2019}, url={https://reference.wolfram.com/language/ref/LearnDistribution.html}, note=[Accessed: 21-December-2024 ]}