常微分方程式
はじめに
純科学・応用科学で関心の対象となる常微分方程式の研究における主要分野が4つある.
- 厳密解.与えられた問題を満足する閉形式の式,または陰的な解析式
- 数値解.厳密解より広範なクラスの問題で利用できるが,通常限定された範囲の独立変数でのみ有効
- 定性的理論.解の全体の特性に関与し,現代の力学系へのアプローチでは特に重要
- 存在定理と一意性定理.1組の条件が微分方程式で満足されるなら,ある望ましい特性を持つ解が存在するということが保証される
この4つの分野のうち,厳密解の研究の歴史が一番長く,ニュートン(Isaac Newton)とライブニッツ(Gottfried Wilhelm von Leibniz)が微積分を発見した直後にまでさかのぼる.以下の表は,DSolveで解くことのできる方程式の種類をリストしたものである.
方程式名
|
一般形式
|
発見年
|
数学者
|
| 分離系 | 1691 | ライブニッツ | |
| 同次 | 1691 | ライブニッツ | |
| 一階線形常微分 | 1694 | ライブニッツ | |
| ベルヌーイ(Bernoulli) | 1695 | ベルヌーイ | |
| リッカティ(Riccati) | 1724 | リッカティ | |
| 一階厳密常微分 | 1734 | オイラー | |
| クレロー(Clairaut) | 1734 | クレロー | |
| 定数係数線形 | 1743 | オイラー | |
| 超幾何 | 1769 | オイラー | |
| ルジャンドル(Legendre) | 1785 | ルジャンドル | |
| ベッセル(Bessel) | 1824 | ベッセル | |
| マシュー(Mathieu) | 1868 | マシュー | |
| アーベル(Abel) | 1834 | アーベル | |
| キーニ(Chini) | 1924 | キーニ |
これらの各タイプに属する常微分方程式の例は,別のチュートリアルに記載されている(表のリンクをクリックすると,関連した例題が開く).
一階常微分方程式
通常の積分
変数分離形微分方程式
変数が分離できるときでも,最終解ではSolveの警告メッセージが表示されることや,InverseFunctionオブジェクトとしてのみ与えられることがある.
同次方程式
一階線形方程式
逆線形方程式
与えられた常微分方程式が ![]() では線形ではないが,
では線形ではないが,![]() では線形と見られることがある.このような方程式を逆線形の常微分方程式と言う.
では線形と見られることがある.このような方程式を逆線形の常微分方程式と言う.
ベルヌーイ(Bernoulli)方程式
ベルヌーイ方程式は,次の形式
の一階線形常微分方程式である.この型の方程式を解く問題は,1695年にベルヌーイによって提示された.その1年後の1696年に,ライプニッツ(Leibniz)は,変数を変えることにより,それが線形方程式に簡約できるということを示した.
一般にベルヌーイ方程式の解は,![]() 個の分岐で構成される.ここで
個の分岐で構成される.ここで ![]() は方程式に含まれる
は方程式に含まれる ![]() の次数である.
の次数である.
リッカティ(Riccati)方程式
リッカティ方程式は,以下の形式
である二階線形常微分方程式である.この方程式は,リッカティ(1776-1754)が二階常微分方程式を解くときの助けとして使ったものである.
リッカティ方程式を解くことは,線形常微分方程式を解くのよりも難しい.
リッカティ方程式はすべて二階線形常微分方程式に変換できる.二階線形常微分方程式が明示的に解ける場合は,リッカティ方程式の解を導くことができる.
厳密方程式
方程式が厳密でないときは,方程式を厳密形に変換する積分因子(すでに定義した関数PおよびQの乗数)を見付けることができる.このような場合,DSolveはさまざまな手法を使って自動的に積分因子を見付けようと試みる.
クレロー(Clairaut)方程式
クレロー方程式は,以下の形式
の一階常微分方程式である.この非線形方程式の際立った特徴は,一般解が非常に簡単な形式となるという点である.
アーベル(Abel)方程式
アーベルの常微分方程式は,以下の形式
である一階の方程式である.この方程式は,ニールス・アーベル(Niels Henrik Abel)が楕円関数理論について研究していろ時に発見されたものであり,リッカティ方程式の自然な一般化を表す.
アーベルの常微分方程式はすべて,方程式![]() の係数,および独立・従属変数への座標変換における不変式から構築される式の列に関連している.これらの不変式は各方程式の特徴を示しており,アーベル常微分方程式の積分可能なクラスを見付けるのに利用することができる.特に,ゼロあるいは一定の不変式を持つアーベルの常微分方程式は簡単に積分でき,その方程式の重要な積分可能クラスを構成する.
の係数,および独立・従属変数への座標変換における不変式から構築される式の列に関連している.これらの不変式は各方程式の特徴を示しており,アーベル常微分方程式の積分可能なクラスを見付けるのに利用することができる.特に,ゼロあるいは一定の不変式を持つアーベルの常微分方程式は簡単に積分でき,その方程式の重要な積分可能クラスを構成する.
積分可能なアーベルの常微分方程式の重要なクラスとして,非線形の座標変換を使った一階逆線形常微分方程式に還元できるクラスがある.
積分可能なアーベルの常微分方程式の重要な別のクラスとして,逆リッカティ方程式に変換できるクラスがある.リッカティ方程式は二階線形常微分方程式に変換できるので,このクラスの解は通常,AiryAiやBesselJ等の特殊関数で与えられる.
ここまでのアーベルの常微分方程式は,第一種と考えられる.第二種のアーベル常微分方程式は,以下の一般系で与えられる.
第二種のアーベル常微分方程式は,座標変換を施した第一種アーベル方程式に変換できる.従って,第二種アーベル方程式の解法は,第一種方程式の解法と同じである.
キーニ(Chini)方程式
キーニ方程式は,アーベル方程式とリッカティ方程式を一般化したものである.
特異解
DSolveはデフォルトでは,線形または非線形の常微分方程式の任意のパラメータに基づいて一般解を返す.クレローの方程式やロジスティック方程式等の非線形常微分方程式では,特異解があるものもある.このような特異解は一般解で任意の定数に特定の値を割り当てて得ることはできないが,力学系の研究等で便利である.
DSolveのオプションIncludeSingularSolutionsTrueを使うと,一般解とともに非線形常微分方程式の特異解が返される.
二階線形常微分方程式
概要
一階線形常微分方程式を解くのは単純であり,必要なのは適切な積分因子を使うことだけである.これとは著しく対照的に,二階線形常微分方程式を扱うために使えるメソッドは多数ある.しかしこのクラスに属する一般方程式の解はまだ求められない.従って,ここでは二階非線形常微分方程式に入る前に,線形の場合について詳述する.
ここで,![]() ,
,![]() ,
,![]() は
は ![]() の任意関数である.「線形」とは
の任意関数である.「線形」とは ![]() ,
,![]() ,
,![]() の各項の次数が1であるという意味である(よって,
の各項の次数が1であるという意味である(よって,![]() あるいは
あるいは ![]() 等の項があると,方程式は非線形になる).
等の項があると,方程式は非線形になる).
定数係数二階線形微分方程式
二階線形常微分方程式の最も簡単なものは,定数係数方程式である.
一般解は2つの指数関数の線形結合である.任意定数C[1]とC[2]は特殊解を生成するために変化させることができる.
基底![]() の指数
の指数![]() と
と![]() は,関連した二次方程式を解くことにより求められる.この二次方程式は,補助方程式あるいは特性方程式と呼ばれる.
は,関連した二次方程式を解くことにより求められる.この二次方程式は,補助方程式あるいは特性方程式と呼ばれる.
この場合,根は実数で異なったものである.これとは別に,実数の重根,虚数根の2つの場合が考えられる.
オイラー(Euler)方程式とルジャンドル(Legendre)方程式
オイラー方程式は,定数係数方程式に変換することで解くことができる.
ルジャンドル方程式は,オイラー方程式を一般化したもので,以下の形式の常微分方程式である.
厳密な二階線形方程式
が成り立つ場合,「厳密である」と言われる.厳密な二階線形常微分方程式は,一階線形常微分方程式に還元することにより解くことができる.
特殊関数を含む解を持つ方程式
DSolveでは,応用数学で見られるほとんどの標準の二階線形常微分方程式の解が見付けられる.
これらの特殊関数は,そのパラメータの特定の値に対する初等関数で表すことができる.Wolfram言語は可能な限り自動的にこの変換を実行する.
この変換の結果,ある常微分方程式の解は部分的に初等関数で表すことができる.エルミート(Hermite)方程式はそのような常微分方程式のひとつである.
有理係数を持つ二階線形常微分方程式
ベッセル関数やルジャンドル関数等の多くの重要な関数は超幾何関数の特殊形なので,超幾何関数は数学解析で統合的な役割を果たす.各超幾何関数は,有理係数を持つ線形常微分方程式と関連している.
DSolveは,二階線形常微分方程式を超幾何関数の常微分方程式に還元することによって,そのクラスの多くを解くことができる.還元には,独立変数と従属変数両方の座標変換が関与する.
特殊関数の常微分方程式は,18世紀から研究されている.この30年の間に,有理係数を持つ常微分方程式を系統的に解くためのパワフルなアルゴリズムが開発されてきた.このタイプのアルゴリズムで重要なものに,コバシック(Kovacic)法がある.これは,与えられた常微分方程式の解をリュービル(Liouvillian)関数で生成するか,与えられた常微分方程式がリュービル解を持たないことを証明するかのどちらかを行う決定手続きである.
コバシック法で返される解には,ExpIntegralEi等の関数や初等関数の未評価の積分が含まれることがある.その理由は,二階線形常微分方程式のひとつの解が分かった後で,第2解を見付けるのは簡単であるが,第2解を求めるのに関与する積分は,明示的に評価するのが難しいためである.
一般に,有理数係数を持つ二階以上の線形常微分方程式の解は,DifferentialRootオブジェクトで与えられる.これはRootによる多項方程式の解に似ている.
非有理係数を持つ方程式
実践的な応用分野で生じる常微分方程式には,非有理係数が含まれることがよくある.そのような場合,DSolveは適切な座標変換を使って,方程式を有理係数を持つ方程式に変換しようと試みる.
二階線形非同次方程式
与えられた二階常微分方程式が非同次ならば,DSolveはその問題の解を返すために「定数変化法」か「未定係数法」を適用する.
定数係数を持つ非同次の線形常微分方程式を解く場合,非同次項が![]() (
(![]() と
と ![]() は
は ![]() の多項式関数)という形式およびその部分形式ならば,未定係数法が使われる.
の多項式関数)という形式およびその部分形式ならば,未定係数法が使われる.
二階非線形常微分方程式
である.ここで,この方程式を最高階数の導関数 ![]() について解くと以下が得られるとする.
について解くと以下が得られるとする.
二階非線形常微分方程式には,解が簡単に見付けられるクラスがいくつかある.
最初のクラスは,明示的には ![]() に依存しない方程式である.つまり,
に依存しない方程式である.つまり,![]() という形式の方程式である.このクラスの方程式は,
という形式の方程式である.このクラスの方程式は,![]() において一階常微分方程式とみなすことができる.
において一階常微分方程式とみなすことができる.
二階線形常微分方程式の場合と同じように,解は2つの任意パラメータC[1]とC[2]に依存する.
簡単に解ける二階非線形方程式の2つ目のクラスは,![]() にも
にも ![]() にも明示的に依存しない方程式である.つまり,
にも明示的に依存しない方程式である.つまり,![]() という形式の方程式である.このクラスの方程式は独立変数
という形式の方程式である.このクラスの方程式は独立変数 ![]() を持つ一階常微分方程式に還元できる.
を持つ一階常微分方程式に還元できる.![]() の最終解を与えるには,逆関数が必要である.
の最終解を与えるには,逆関数が必要である.
3つ目のクラスは,![]() に明示的に依存しない方程式である.つまり,
に明示的に依存しない方程式である.つまり,![]() という形式の方程式である.これもまた,独立変数
という形式の方程式である.これもまた,独立変数 ![]() を持つ一階常微分方程式に還元できる.
を持つ一階常微分方程式に還元できる.
4つ目のクラスは,変数 ![]() ,
,![]() ,
,![]() のどれか,あるいはすべてが同次である方程式である.この場合は,いくつかの例が考えられるが,ここでは以下に挙げる簡単な例だけを考える.
のどれか,あるいはすべてが同次である方程式である.この場合は,いくつかの例が考えられるが,ここでは以下に挙げる簡単な例だけを考える.
最後,5番目のクラスは,厳密な方程式,あるいは積分因子を使って厳密にすることができる方程式である.
極めて単純に見える非線形常微分方程式の解が複雑であることがある.そのような場合の解を検証・適用することは難しい問題である.
高階常微分方程式
概要
二階常微分方程式の場合と同様,高階常微分方程式も線形・非線形の分類ができる.![]() 階線形常微分方程式は,以下のような一般形を持つ.
階線形常微分方程式は,以下のような一般形を持つ.
![]() がゼロ関数ならば,方程式は同次であるという.このセクションは,主に同次方程式に限定する.
がゼロ関数ならば,方程式は同次であるという.このセクションは,主に同次方程式に限定する.
二階線形常微分方程式の解法の多くは,![]() 階(
階(![]() は2より大きい)線形常微分方程式に一般化することができる.常微分方程式の階数が重要でない場合は,単に線形常微分方程式という.
は2より大きい)線形常微分方程式に一般化することができる.常微分方程式の階数が重要でない場合は,単に線形常微分方程式という.
定数係数高階線形常微分方程式
定数係数線形常微分方程式は,補助方程式(特性方程式)の根が分かると,簡単に解くことができる.以下にその例を挙げる.
高階のオイラー方程式とルジャンドル方程式
ルジャンドル方程式は,オイラー方程式を一般化したものである.これは次の形式である.
厳密な高階方程式
が成り立つときに「厳密である」といわれる.厳密さの条件は,問題を階数 ![]() の方程式を解くことに還元するために使うことができる.
の方程式を解くことに還元するために使うことができる.
その他の高階方程式
多くの二階常微分方程式の解は特殊関数で表すことができる.一定の高階常微分方程式の解は,AiryAi,BesselJ等の特殊関数を使って表すこともできる.
二階線形常微分方程式の場合と同様に,有理係数を持つ高階常微分方程式を解く現代的アルゴリズムがある.このようなアルゴリズムは,有理関数と,有理関数の積分の指数関数との組合せである「有理数指数」解を与える.アルゴリズムは,与えられた常微分方程式の完全解を求めるために階数の減少等の技法と組み合せられる.
ここまでに提示した方程式は同次方程式である.つまり,方程式に ![]() あるいはその導関数を持たない項がない.与えられた常微分方程式が非同次ならば,DSolveは「定数変化法」か「未定係数法」を適用して解を得る.
あるいはその導関数を持たない項がない.与えられた常微分方程式が非同次ならば,DSolveは「定数変化法」か「未定係数法」を適用して解を得る.
従って,非同次方程式の一般解は,同次方程式の一般解と常微分方程式の特殊積分との和である.
高階非線形常微分方程式の解法は,問題を低階に還元することにかなり依存している.
常微分方程式系
はじめに
常微分方程式系は,電気学や生物資源学等のさまざまな科学分野で重要である.常微分方程式系も単独常微分方程式のように,線形・非線形に分類することができる.
ここで ![]() は未知関数のベクトル,
は未知関数のベクトル,![]() は未知関数の係数行列,
は未知関数の係数行列,![]() は系の非同次部を表すベクトルである.
は系の非同次部を表すベクトルである.
二次元の場合,系は以下のようにより具体的に書き表すことができる.
行列 ![]() の要素がすべて定数であるなら,系は定数係数線形系という.
の要素がすべて定数であるなら,系は定数係数線形系という.![]() が零ベクトルならば,同次系という.
が零ベクトルならば,同次系という.
線形系の解の重要な全体特性は,定数係数同次常微分方程式系を考えることで明確になる.
線形常微分方程式系
線形常微分方程式系もベクトル変数と行列変数を使って行列形式で解くことができる.
定数係数を持つ任意階の同次常微分方程式は,簡単に解ける.このような方程式は,一階常微分方程式系に変換して解く.
一般に,非定数係数線形常微分方程式系は,次の例で示すように,係数行列が単純な構造である場合にのみ解くことができる.
単独常微分方程式の場合と同様に,有理係数を持つ常微分方程式系を解くためにも高度なアルゴリズムが使える.
ここまでの系はすべて同次であった.系が非同次(つまり,従属変数およびその導関数を含まない項がある場合)ならば,DSolveは定数変化法か未定係数法を適用して,一般解を見付ける.
非同次系の特殊解は,定数C[1]およびC[2]に値を割当てることで得られる.
非線形常微分方程式系
以下で,DSolveを使って記号的に解くことのできる非線形常微分方程式系の例を2つ挙げる.
上記2つの例により,かなり単純な系の解は通常独立変数の複雑な式となることが分かる.実際,解は陰形式でのみ求められることがよくあるので,InverseFunctionオブジェクトや未評価のSolveオブジェクトを含むことがある.
Lie対称性による非線形常微分方程式の解法
1870年ごろ,Lie (Marius Sophus Lie)は,微分方程式を解くための方法の多くを群論で統合できることを発見した.Lie対称性による解法は,現在の非線形常微分方程式の研究において中心的アプローチとなっている.Lie対称性による解法では,対称性の概念を使って系統的に解を生成する.ここではLieのアプローチを簡単に紹介し,DSolveがこの方法を使って解く例題を挙げる.
Lieの解法の主要な概念は,対称群の無限小生成作用素というものである.この概念は以下の例で示す.
![]() が固定値のとき,点
が固定値のとき,点![]() (青)は
(青)は![]() (赤)と原点を結ぶ直線を角度
(赤)と原点を結ぶ直線を角度 ![]() まで,反時計回りに回転させることで得ることができる.
まで,反時計回りに回転させることで得ることができる.
Lie対称性による解法では,群の一次近似式を計算する必要がある.この近似式が無限小生成作用素と呼ばれるものである.
回転群は幾何オブジェクトの対称性の研究で生じるもので,対称群の一例である.無限小生成作用素(微分演算子)は,この対称群を簡単に局所表現するもので,行列の集合の形式を取る.
無限小生成作用素の動作により0に還元された式は,群の不変式と呼ばれる.
ここで,リッカティ方程式は3つの変数 ![]() ,
,![]() ,
,![]() に依存する.ゆえに,無限小生成作用素
に依存する.ゆえに,無限小生成作用素 ![]() は,この一次方程式の3つの変数すべてに作用するよう拡張しなければならない.
は,この一次方程式の3つの変数すべてに作用するよう拡張しなければならない.
対称性(無限小生成作用素の形式)は,与えられた方程式の次数によって,3通りに使うことができる.
- 方程式の次数が1の場合,方程式を厳密・可解にする常微分方程式の積分因子を与える.
- 方程式が簡単な(積分可能な)形式となる正準座標集合を与える.
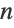 階常微分方程式を解く問題を
階常微分方程式を解く問題を  階常微分方程式を解く問題に還元する.後者は通常前者よりも簡単である.
階常微分方程式を解く問題に還元する.後者は通常前者よりも簡単である.
関数DSolveは与えられた常微分方程式に標準的な種類の対称性があるかどうかをチェックし,それを使って解を返す.以下は,DSolveがこのような対称性による解法を使う常微分方程式の3つの例である.
分数階微分方程式
分数階微分方程式(FDE)は分数階の微積分 ![]() を含む微分方程式である.これらは注目を集めてきた,工学,物理学,化学,生物学等の分野で広く使われる常微分方程式の一般化である.
を含む微分方程式である.これらは注目を集めてきた,工学,物理学,化学,生物学等の分野で広く使われる常微分方程式の一般化である.
DSolveは,Caputo微積分CaputoDを含む定数係数を持つ線形分数階微分方程式を解くことができる.
解はMittagLefflerE関数で与えられる.これは分数階微積分の応用では基本的な関数である.これが分数階微分方程式の解で果たす役割は常微分方程式の解に対するExp関数の役割および重要性と似ている.定数係数を持つ分数階微分方程式はどれもMittag–Leffler関数で解くことができる.
Caputo型の分数階微分方程式では,初期条件は常に従属変数の整数階微分に対して与えられる.初期条件の数は分数階微分方程式の階数 ![]() によって異なり,
によって異なり,![]() に等しい.
に等しい.
DSolveは定数係数を持つ線形分数階微分方程式系を解くこともできる.この系の方程式はすべて同じ階数 ![]() を持たなければならない.
を持たなければならない.