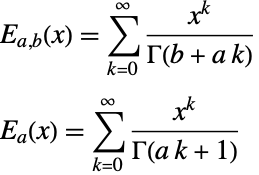分数阶微积分
引言
分数阶微积分是任意实数阶或复数阶微分及积分理论的发展. 它将经典微积分的基本运算扩展到分数阶,研究涉及这些分数阶导数和积分的微分方程的求解方法[1].
分数阶微积分不仅仅是一个纯粹的数学理论. 这一分支在扩散问题、流体动力学、控制理论、信号处理等领域越来越受重视. 许多科学现象都是用分数微分方程、积分方程和混合方程来描述的. 因此,鉴于这个主题的重要性和潜力,我们开发了用于探索 Wolfram 语言中分数阶微积分生态系统的函数.
简而言之:分数阶微积分能够将任何积分或微分方程推广到其“分数”类似物的无限集(其中涉及分数阶积分和导数). 因此,它扩展了描述新的物理现象并提高现有模型准确性的可能性.
分数阶微积分简史
微积分的基础是由牛顿和莱布尼茨在 17 世纪奠定的,其中整数阶微分和积分是这门学科的两个基本运算.
1695 年,莱布尼茨在给洛必达的信中写下了半阶导数的含义. 尼尔斯·阿贝尔推动了这种分数阶微积分理论,他在 1823 年和 1826 年写了两篇文章,其中可以找到该理论的所有要素:分数阶积分和微分的思想,它们之间的互逆关系,以及将分数阶微分和积分理解为是相同的广义运算等.
阿贝尔考虑了等时线问题的广义版本(也称为阿贝尔问题),其中积分方程 ![]() 对于给定的传输时间函数
对于给定的传输时间函数 ![]() 作为距离
作为距离 ![]() 的函数求解. 未知函数
的函数求解. 未知函数 ![]() 的确定使得找到等时曲线本身的方程成为可能.
的确定使得找到等时曲线本身的方程成为可能.
经过几次代数运算后,这个积分方程可以改写为 ![]() 的形式,这就是现在所谓的半阶 Caputo 分数阶导数 [2].
的形式,这就是现在所谓的半阶 Caputo 分数阶导数 [2].
直到二十世纪下半叶,分数阶微积分主要是作为一种抽象的数学理论发展起来的. 在过去的几十年里,来自不同领域和背景的科学家都在从不同的角度研究这一理论及其应用,并确实获得了许多实际应用. 关于如何定义分数“微分积分”运算有不同的方法,但其中三种是最流行的.
什么是分数阶微积分?
积分本质上是微分的逆运算,因此定义一个微分/积分的联合运算,即所谓的微分积分,是可能的:在文献中,该算子被写作 ![]() . 这里微分/积分的顺序由参数
. 这里微分/积分的顺序由参数 ![]() 给出,理论上它可以是任何实数或复数. 如果是正整数,则归约为普通微分; 如果是负整数,则归约为普通积分.
给出,理论上它可以是任何实数或复数. 如果是正整数,则归约为普通微分; 如果是负整数,则归约为普通积分.
此外,分数微分取决于函数 ![]() 在点
在点 ![]() (下限)的值:它是描述函数“历史”的附加参数. 在实践中,通常将下限取为 0,以便分数阶导数/积分包括原点处的函数值; 这对于解决初值问题很有用.
(下限)的值:它是描述函数“历史”的附加参数. 在实践中,通常将下限取为 0,以便分数阶导数/积分包括原点处的函数值; 这对于解决初值问题很有用.
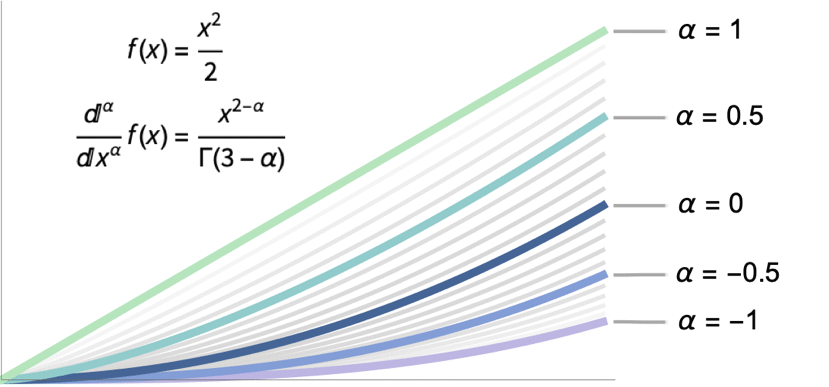
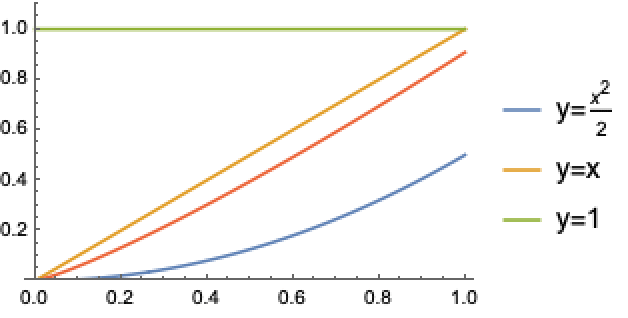
分数阶微积分理论最重要的出发点是,无论分数阶微分积分算子的定义如何,它都应该与整数 ![]() 的普通微分/积分算子一致. 下图是平方函数及其普通和分数阶导数和积分的图线:
的普通微分/积分算子一致. 下图是平方函数及其普通和分数阶导数和积分的图线:
平方函数的分数阶导数
众所周知,平方函数 ![]() 的一阶导数是
的一阶导数是 ![]() ,其积分是
,其积分是 ![]() ,但这个函数的半阶导数是多少? 或者其逆运算,函数的半阶积分是多少?
,但这个函数的半阶导数是多少? 或者其逆运算,函数的半阶积分是多少?
显然,这是通过两次“半阶分数微分”过程获得的平方函数的一阶导数. 此外,可以很容易地验证平方函数的反导数可以通过两个类似的半阶积分过程获得(在前面显示的公式中代入 ![]() ). 上面显示的运算正是平方函数的分数阶微分.
). 上面显示的运算正是平方函数的分数阶微分.
分数微分积分的定义
1. Grünwald–Letnikov 方法 . Grünwald–Letnikov 微积分 给出经典微分/积分的明显扩展并且基于极限:
在实践中,这种方法不是很有用,因为它包含函数在不同点的无限数量的近似值. 它的计算有各种高级算法来实现 [3],但从实用的角度来看,这些算法的计算量很大.
2. Riemann–Liouville 微积分 . Riemann–Liouville 定义 为:
Riemann–Liouville 方法具有分数阶微积分数学理论坚实而严格的基础. 这个理论得以良好的发展,但是 Riemann–Liouville 方法有一些局限性,使其不适合在实际问题中的应用; 但是,它在理论方面非常重要.
这与 Riemann–Liouville 微积分有相似之处. 实际上,Caputo 微积分可以通过 Riemann–Liouville 法来定义:
根据定义,Caputo 分数阶导数与负数阶 ![]() 的 Riemann–Liouville 分数导数一致.
的 Riemann–Liouville 分数导数一致.
微积分的 Caputo 定义与 Riemann–Liouville 或 Grünwald–Letnikov 的定义相比有很多优点:首先,它考虑了函数及其导数在原点处的值(或者,一般来说,在任何下限处 ![]() ),自动使其适用于使用拉普拉斯变换求解分数阶初值问题. 此外,常数的 Caputo 分数阶导数为 0(而一般而言,Riemann–Liouville 分数阶导数并非如此),因此它更符合经典微积分.
),自动使其适用于使用拉普拉斯变换求解分数阶初值问题. 此外,常数的 Caputo 分数阶导数为 0(而一般而言,Riemann–Liouville 分数阶导数并非如此),因此它更符合经典微积分.
下面的动画显示了平方函数的 Caputo 分数阶导数与普通函数的行为比较——可以看出,分数阶导数在整数阶之间插值并且与微积分整数阶的常导数一致:
Wolfram 语言中的分数阶微积分
Wolfram 语言包括 FractionalD 和 CaputoD 函数,分别代表 Riemann-Liouville 和 Caputo 分数阶微积分 [4-5]. 这些函数对分数阶导数 ![]() 和
和 ![]() 进行符号式计算.
进行符号式计算.
FractionalD 函数
这是一个玩具示例,展示了分数阶导数可能的推导规则. 使用 Riemann–Liouville 定义计算三次函数的半阶分数阶导数:
上述输入只是分数微分的 Riemann-Liouville 定义的直接应用. 现在使用内置的 FractionalD 函数验证此结果:
以下计算使用三个嵌套的分数阶积分复原初始函数(普通积分与三次 1/3 阶分数阶积分相同):
现在计算这个三次函数的任意分数阶导数,制作一个特定阶数的表并绘制导数列表:
接下来,计算 Exp 和 BesselJ 函数的 0.23 阶分数阶导数:
MeijerG 的分数阶导数以另一个 MeijerG 函数的形式给出:
上述情况是一个非常重要的理论特征,可用于通过由另一个内置 MeijerGReduce 函数获得的 MeijerG 表示来生成复杂函数的 FractionalD 规则.
作为最后一个示例,下表给出了一些常见特殊函数的 ![]() 阶 Riemann–Liouville 分数导数和
阶 Riemann–Liouville 分数导数和 ![]() 阶普通导数:
阶普通导数:
CaputoD 函数
CaputoD 函数给出 Caputo 分数阶导数 ![]() . 这是一个在实际应用中更有用的函数,因为根据其理论定义,它考虑了原点处的函数.
. 这是一个在实际应用中更有用的函数,因为根据其理论定义,它考虑了原点处的函数.
一个基本的重要特征是常数的 Caputo 分数阶导数为 0(而 Riemann–Liouville 导数不是):
对于 ![]() 的负数阶,CaputoD 输出与 FractionalD 一致,这只是因为它们的定义:
的负数阶,CaputoD 输出与 FractionalD 一致,这只是因为它们的定义:
现在,计算 Exp 函数的 0.23 阶 Caputo 分数阶导数:
计算 BesselJ 函数的半阶 Caputo 分数阶导数:
作为最后一个示例,下表给出了一些常见数学函数的半阶 Caputo 分数阶导数:
数值分数阶微积分
FractionalD 和 CaputoD 是重要且相当强大的函数,但由于其定义的复杂性(函数的积分的导数或导数的积分乘以其他幂函数),计算可能非常耗时,并且可能会产生繁琐的输出. 另一种情况是,对于种类繁多的输入,内置的积分方法无法生成任何输出. 以下情况是一个示例,其中 FractionalD 生成的输出包含 DifferenceRoot 函数给出的一般完整序列:
这些符号式函数具有数值式对应是有利的:Integrate 的数值对应是 NIntegrate,DSolve 的数值对应是 NDSolve,等等. 类似地,基于 [1] 和 [3] 中介绍的不同算法,FractionalD 和 CaputoD 的数值对应分别为 NFractionalD 和 NCaputoD 函数. 这些函数的设计很简单——它们只是生成一个数值输出,对应于给定点处给定阶数的分数阶导数的值. 在以下示例中,平方函数的半阶分数阶导数的值在点 ![]() 处计算:
处计算:
使用这些函数,可以深入了解分数阶导数的行为(例如,通过绘图). 作为示例,考虑本章的第一个输出,在输出中包含 DifferenceRoot. 一般来说,![]() 函数的分数阶导数涉及哪些函数是未知的. 然而,通过 NFractionalD 或 NCaputoD 函数绘制这个分数阶导数的图形,可以帮助我们更好地理解:
函数的分数阶导数涉及哪些函数是未知的. 然而,通过 NFractionalD 或 NCaputoD 函数绘制这个分数阶导数的图形,可以帮助我们更好地理解:
这是另一个涉及 NCaputoD 函数的示例:
此外,分数微分和积分的 Grünwald–Letnikov 方法在 NFractionalD 中可用:
事实上,这在数值上对应于 Riemann–Liouville 结果:
分数阶拉普拉斯变换
拉普拉斯变换和 MittagLefflerE 函数在求解包含分数阶导数和积分的微分方程中起着至关重要的作用. 下面给出了有关 MittagLefflerE 的一些基本信息,并介绍了通过 LaplaceTransform 求解分数阶微分方程 (FDE) 的方法.
MittagLefflerE 函数是指数函数的自然推广:正如任何具有常系数的 ODE 在指数函数中求解一样,任何具有常系数的 FDE 也在 MittagLefflerE 函数中求解. 以下是普通和广义 MittagLefflerE 函数的定义:
指数函数是 MittagLefflerE 的特例:
MittagLefflerE 函数的拉普拉斯变换可以使用 Wolfram 语言计算:
LaplaceTransform 将时域 MittagLefflerE 转换为频域,也称为 ![]() 域:
域:
应用 InverseLaplaceTransform,复原了初始 Mittag–Leffler 函数:
一整类 ![]() 域函数被逆拉普拉斯变换为包含 Mittag–Leffler 函数的
域函数被逆拉普拉斯变换为包含 Mittag–Leffler 函数的 ![]() 域表达式:
域表达式:
可以使用 LaplaceTransform 复原初始的 ![]() 域函数:
域函数:
众所周知,整数阶导数的拉普拉斯变换技术对于求解整数阶微分方程起着重要作用. 这是因为,例如,二阶导数的 LaplaceTransform 可以用函数的 LaplaceTransform 表示:
分数阶导数的 LaplaceTransform 也有类似的性质. 例如,这是 3/2 阶 CaputoD 导数的 LaplaceTransform:
现在,可以使用此性质来计算正弦函数的 Caputo 导数的拉普拉斯变换:
如果首先计算正弦函数的 CaputoD,然后将 LaplaceTransform 应用于输出,可以获得相同的结果:
第一种方法的优点是只需要计算 Sin 函数的 LaplaceTransform,而在第二种方法中,必须求解更复杂的 HypergeometricPFQ 函数的 LaplaceTransform,该函数出现在 Sin 的 CaputoD 过程中.
分数阶微分方程
分数阶微分方程 (FDE) 是涉及分数阶导数的微分方程 ![]() . 这些方程是常微分方程 (ODE) 的推广,受到人们的广泛关注,并广泛应用于工程、物理、化学、生物学等领域.
. 这些方程是常微分方程 (ODE) 的推广,受到人们的广泛关注,并广泛应用于工程、物理、化学、生物学等领域.
作为第一步,考虑具有常系数的线性分数阶 ODE. 与 ODE 的情况一样,可以使用 LaplaceTransform 将初始分数阶微分方程变换为 ![]() 域中的某个代数方程并求解. 然后使用 InverseLaplaceTransform 得到初始分数阶微分方程的时域解. 这个过程如下所示.
域中的某个代数方程并求解. 然后使用 InverseLaplaceTransform 得到初始分数阶微分方程的时域解. 这个过程如下所示.
首先在具有一些初始值的分数阶微分方程的两边应用 LaplaceTransform:
然后对 LaplaceTransform 求解:
最后,应用 InverseLaplaceTransform 得到时域解:
可以使用 DSolve 直接导出该解:
DSolve 能够求解任何具有常系数的线性 FDE. 下面是一个半阶 FDE 的例子:
对于 Caputo 型 FDE,初始条件将针对整数阶导数给出. 初始条件的数量取决于 FDE 的阶数 ![]() ,等于
,等于 ![]() . 下面是前面示例的初始值问题的解:
. 下面是前面示例的初始值问题的解:
DSolve 还可以处理一些具有常系数的 FDE 线性系统. 系统中的所有方程式必须具有相同的阶数 ![]() . 例如:
. 例如:
作为最后一个示例,这里是使用向量变量的三个 FDE 组成的方程组的解:
应用
近年来,分数阶微积分开始在不同的科学领域获得越来越多的应用. 这里是一些范例.
分数阶谐振子
这个例子清楚地表明,FDE 的阶数可以用作控制参数来模拟一些复杂的系统.
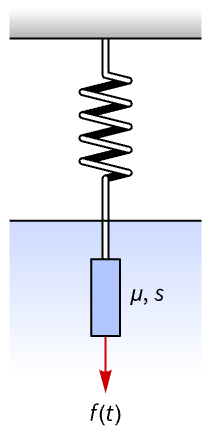
具有分数阻尼的动力系统
考虑一个动力系统,该系统由质量为 ![]() 、面积为
、面积为 ![]() 的薄板组成,该薄板浸没在密度为
的薄板组成,该薄板浸没在密度为 ![]() 、粘弹性常数为
、粘弹性常数为 ![]() 的无限延伸的牛顿流体中,通过劲度系数为
的无限延伸的牛顿流体中,通过劲度系数为 ![]() 的弹簧连接到一个固定点. 假设板的表面足够大,以至于流体减慢了板的运动.
的弹簧连接到一个固定点. 假设板的表面足够大,以至于流体减慢了板的运动.
该系统可以通过具有分数阻尼的二阶微分方程建模,使用参数 ![]() 和
和 ![]() [6]:
[6]:
分数阶 LC 电路
分数阶 RC 电路
分数阶波动方程
DSolve 可以对其求解:
小结
如今,分数阶微积分受到越来越广泛地关注,因为它将众所周知的积分微分方程推广到包含目标函数的分数阶导数或积分的更广义的方程,能够更精确地描述现实世界中的不同现象.
有鉴于此,Wolfram 语言纳入了两个用于分数阶微积分的基本运算符(FractionalD 和 CaputoD 函数). 并付出巨大的努力来增加对通过 DSolve 与 LaplaceTransform 求解分数阶微分方程的支持.
Wolfram 语言还包括使用 NFractionalD 和 NCaputoD 对分数微分积分的数值支持. NFractionalD 具有两种内部方法,分别代表 Riemann–Liouville 和 Grünwald–Letnikov 分数阶微积分,应该足以满足大多数实际应用场景.
参考文献
1. Oldham, K. B. and J. Spanier. The Fractional Calculus: Theory and Applications of Differentiation and Integration to Arbitrary Order. Academic Press, 1974.
2. Podlubny, I., Magin, R. and I. Trymorush. "Niels Henrik Abel and the Birth of Fractional Calculus." Fractional Calculus and Applied Analysis 20, no. 5 (2017): pp. 1068–1075.
3. Li, C. and M. Cai. Theory and Numerical Approximations of Fractional Integrals and Derivatives. SIAM, 2019.
4. New in Wolfram Language 13.1 webinar series.
5. T. Ishkhanyan. "Fractional Calculus in Wolfram Language 13.1" blog post.
6. Kilbas A., Srivastava, H. M. and J. J. Trujillo. Theory and Applications of Fractional Differential Equations. Elsevier, 2006.