Wolfram言語における数の四則演算は電卓と同様にできる．

複数の項からなる式がグループ化されているとき，数学で標準的な優先順位に従って計算が行われる．例えば，2^3+4は(2^3)+4に等しいが，2^(3+4)には等しくない．丸カッコを使えば計算の優先順位を制御することができる．

Wolfram言語では，通常の計算よりも高い特定の精度で計算を実行することができる．厳密な数値が与えられると，Wolfram言語はそれを近似表現に変換せず厳密な結果を与える．

Wolfram言語の最も重要な機能のひとつに計算結果を正確な代数式で得ることができる，ということがある．最も，解く問題によっては答を「閉じた形」で得ることが数学的にできないときもあるが，そのようなときでも，問題を数値解析手法を用い近似的に解くことは可能である．

定積分のような計算で具体的な結果が見出せなかった場合，結果はシンボル的な記述形で返される．そして，求まったシンボル式にNを適用させることで数値解析で近似解を求めることができる．

積分を数値解析で求めるとき，Integrateを使って求めた積分にNを適用させるといった手順はあまり効率がよいとは言えない．代数的な解法はせずに，始めから関数NIntegrateを使い直接数値的な答を得る方がよい．Integrateを使うと積分が解けないときでも解けないという結果が出るまでそれなりの時間を費やしてしまう．

Wolframシステムにおいて，数値積分に代表される数値解析は代数計算的な解析とかなり違った手法に基づいて行われる．

代数的に積分するようにWolframシステムに積分式を与えると，式は関数形式で取り込まれ，式には積分操作を表すための一連の厳密でシンボル的な変換規則が次々に適用される．そして，積分した結果を評価することで積分処理を終える．

しかしながら，Wolframシステムが数値積分を行う場合，若干の最初の記号的な前処理を除き，積分式に関してWolframシステムが保持する情報は一連の積分式の数値のみである．実際に数値的に積分を決定するために，Wolframシステムは積分式の滑らかさや他の特性に関して事実上ある種の仮定を行わなければならない．十分に病的な被積分関数を与えると，この仮定が有効ではなくなるかも可能性があり，結果としてWolframシステムがこの積分の間違った答を返すこともある．

例えば，積分しようとする関数が特定の位置にスパイク状の幅の狭い突起部を持つとする．Wolframシステムは特定の点で積分式をサンプリングし，それらのサンプリング区間において式が滑らかであるとみなす．ここで，もしサンプリング点が上記の突起部を外れたなら，突起部はないと同然になり，求まる積分には反映されなくなってしまう．

NIntegrateは，被積分関数の数値に関して得られるだけの情報を最大限に利用する．そのため，例えば，特定の領域内で積分誤差が大きいと予測されるときは，NIntegrateはその領域のサンプリング数を増やしている．このようにNIntegrateでは積分式に応じた解析ができるように解析手順の「適応化」が行われている．

NIntegrateの適応化は，少なくともその考え方において，滑らかな曲線を描画するために使うPlotの手順に似ている．いずれの場合も，特定の領域で滑らかな近似が得られるまでサンプリング点を増加させるという考え方に基づいている．

この種の数値積分で遭遇する問題は，他の数値計算でも見られる．

例えば，無限級数の和を近似するとき，まず，Wolframシステムは一定の項までサンプリングし，そのサンプリング値に基づいた外挿処理により残りの項の寄与量を推定しようとする．このため，級数の後の方に大きな項を入れると，その項は検知されずに間違った和が求まってしまうという問題が起る．

関数の最小を近似値で求める場合も同様な問題が起る．つまり，関数が有限数の点においてサンプリングされ，サンプリング区間では関数が滑らかで補間可能なものとみなされる．しかし，特定の領域に急な窪みが存在するとそれは検知されずに間違った最小値が求まってしまうかもしれない．

関数の値を純粋に数値計算手法のみで求めようとする限り，上記の問題は常につきまとう．シンボル的な手法を使い厳密な代数計算をしなければこの問題は回避できない．

したがって，場合によっては，まずシンボル的に問題を解いておき，そうして求まった代数式を数値解析する，という手順が有効にもなり得る．そのような手順を使えば，数値解析だけだと起るような問題が回避できるかもしれない．

NIntegrateの重要な機能のひとつに，既知の点で発散するような関数に対処できることがある．NIntegrateでは積分領域の両端についてこのような問題が起らないか自動的に判定が行われるようになっている．

NIntegrateは，積分領域および被積分関数の区分関数（Piecewise，Abs等）により定義されるすべての部分領域の終点における特異点を自動的に検知しようとする．したがって，両端以外に特異点が存在する場合，NIntegrateの返す答は正しくない可能性がある．それでも，適応化の中でNIntegrateが特異点を検出できるときがある．そのようなときは，警告が発せられる．

もし，積分する関数がどこで特異点を持つかあらかじめ判明していれば，NIntegrateにそのことを伝え，適切な処置を取るように指示することができる．NIntegrate[expr,{x,x_min,x₁,x₂,…,x_max}]とすると，x_min から x_max の区間にある各中間点 x_i において特異点が存在する可能性があるとして式 expr の積分が行われる．

また，NIntegrateに複素平面上の積分路を表す中間点 x_i のリストを与えることもできる．この場合，積分路は x_min から始まり x_i を通って x_max で終る折れ線区間からなるとみなされる．

NIntegrateで数値積分すると，積分式が一連の点でサンプリングされる．その際に特定の領域で積分式に急激な変化が認められると，その領域は細分化され，サンプリングが再帰的に行われ，それと同時にサンプリング点の数が増やされる．パラメータMinRecursionとMaxRecursionを使い，再帰の最大・最小回数が指定できる．MinRecursionの値を増やせば，NIntegrateにおけるサンプリング点の数が必ず増えるようになる．MaxPointsとMaxRecursionは，NIntegrateが使うサンプリング点の数の上限を決定する．MinRecursionまたはMaxRecursionの値を高く取ると，NIntegrateの計算時間が余計にかかるようになる．

多次元の積分をNIntegrateで計算すると，非常に長い時間がかかるときがよくある．そのようなときは，オプションMaxPointsを小さい値に設定しNIntegrateで限られたサンプリングを行うようにすることで，推定的な積分値を求めるようにしたらよいだろう．

NSumでは，まず，いくつかの項が実際に計算され，その結果をもとに残る項の寄与量が推定される．この推定を行うには2つのアプローチが取られる．その1つはオイラー・マクローリン(Euler–Maclaurin)法と呼ばれ，積分をもとに総和を推定する手法に基づいたアプローチである．2番目は，ウィン(Wynn)のイプシロン法として知られ，和の項を余分にサンプリングし，その求めた値をある指数減少関数を掛け合せた多項式にフィット処理する，という手法に基づくアプローチである．3番目のアプローチは級数の交代に有効なもので，符号交代法を用いる．この方法もまた，和の項を余分にサンプリングし，2つの多項式の比からその和を推定する（パデ近似）というものである．

特に評価法を上記の手法のどちらかに指定しなければ，NSumは自動的にEulerMaclaurinかWynnEpsilonのどちらを選択する．どちらを使うにせよ，和を求めようとする関数に特定の仮定がなされる．もし仮定した条件が実際の式に合わないと，答は間違ったものになる．

NSumは，無限大の極限を持った和を求める問題で最もよく使われる．もちろん，有限の極限を持った和にも使える．NSumでは総和を取るオブジェクトに関して特定の条件を仮定することで，Sumで必要になるような大量な関数評価を避けることが可能になる．

NProductは基本的にNSumと同様に機能し，オプションも同じように使う．

方程式が線形関数や多項式からなるとき，NSolveを使うことで，存在するすべての解に対する数値解析的な近似値を得ることが可能である．しかし，より複雑な関数，例えば超越関数を含む方程式においては，一般に体系化された手法がないことから，数値解析でも解を求めることができない．そのような場合でも，FindRootを使い数値解を探索することは可能である．FindRootを使うには，探索の初期値を指定する必要がある．

NSolveを使えば，整方程式あるいは整方程式系なら完全な数値解が求まる．

NSolveは整方程式の解を数値近似するために使う．「一変数の方程式」で説明したように，多項式よりさらに一般化された方程式を数値的に解くことは極めて難しい．それでも，FindRootを使って関数の数値根や，任意な単一方程式・連立方程式の数値解を探索することは可能である．

FindRootを使った解の探索では，指定した初期値の点を始点として，そこから徐々に解に向かって接近していく．複数の方程式を解くときでも，FindRootでは最初に見付かった解だけが返される．見付かった答がどの解に相当するのかは初期値により違ってくる．与えた初期値が特定の解に十分近付いていれば通常はFindRootはその解を求める．

FindRootが使う変数はリストを値として持つことができる．これにより，ベクトルを引数に取る関数の根を求めることができる．

のような代数方程式では，個々の の解は単なる1つの数である．一方，微分方程式では，解は数ではなく関数である．例えば，の方程式では，独立変数 の区間を限定した上で，関数 の近似解を得るようにしたい．

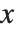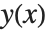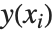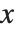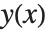Wolfram言語は，関数の近似解をInterpolatingFunctionオブジェクトとして返す．このオブジェクトは，特定の の値に適用されるとき，その点における の近似値を返す関数である．このときInterpolatingFunctionは，の値から構成されるテーブルを保持し，このテーブルで補間することで特定の点 における の近似値を求める．

「微分方程式の数値解法」で説明したNDSolveを使うと，微分方程式を数値解析的に解くことができる．また，単独の微分方程式でも連立の微分方程式でもNDSolveで解ける．さらに，広い範囲の常微分方程式と偏微分方程式の一部が扱える．常微分方程式系の場合，未知の関数 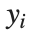がいくつあっても構わないが，すべて単一の独立変数 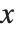のみに依存しているものとする．偏微分方程式の場合は，複数の独立変数を含んでいる．NDSolveは微分方程式と代数方程式が混ざった「微分代数方程式」も扱うことができる．

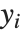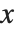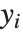NDSolveで求まる関数 の解は，InterpolatingFunctionオブジェクトを使って表される．InterpolatingFunctionオブジェクトは，独立変数 が から で指定される範囲にあるとき の近似を与える．

NDSolveでは解を求めるために反復手法が使われる．それは のある値を始点とし，一連の刻みを取りながら から の範囲をくまなく探索していく．

探索を開始するには，NDSolveの式の中に 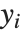とその導関数に関する適切な初期条件や境界条件が備わっている必要がある．これらの条件を与えることで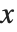， の特定点における 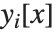，さらに導関数 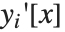の値を決定していく．少なくとも常微分方程式において，この条件は 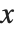のどの点でもよい．それはNDSolveが から の全範囲をくまなく自動的に探すからである．

NDSolveを使う際は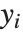， の解を完全に決定するのに十分な初期条件，または，境界条件を与えておく必要がある．DSolveを使って微分方程式の厳密解を求めるときには，初期条件が足りなくてもどうにかなる．これは，指定しなかった初期条件のため発生する自由度を明示化するため，積分定数C[i]がDSolveにより自動的に挿入されるからである．ところが，NDSolveでは解は数値として与えなければならないので，数値では余分に発生する自由度が表せない．このため，解を決定するのに十分な初期条件，または，境界条件を明示的に与えなければならない．

階の微分方程式を解くとき，通常，最大で次までの導関数について初期条件を与えるか，または， 点における境界条件を与える必要がある．

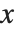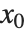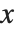多くの場合，与える初期条件は必ず同一の 値，例えば を含む必要がある．このため， から の範囲は別に与えなくてもよくなる． の範囲を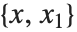として指定すると，Wolfram言語では自動的に 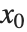から 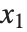の範囲で有効な解が生成される．

初期条件とする方程式はどんな種類のものでもよい．場合によっては，これらの方程式は複数の解を持つことがある．そのような場合は，それに対応した形でNDSolveが複数の解を生成する．

NDSolveを使って，結合された微分方程式の系を解くことも可能である．

微分方程式に未知の関数を使うとき，関数の名前として必ずしも単一のシンボルを与える必要はない．未知の関数が複数個あるとき等は，例えば といった関数名にするとよい．

NDSolveは値がリストや配列である関数も扱える．y[0]=={v₁,v₂,…,v_n}のような初期条件を与えると，NDSolveは を値が長さ のリストである関数だと仮定する．

NDSolveには方程式を解く多くのメソッドが備わっているが，基本的にはすべてのメソッドが独立変数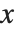 内で一連のステップを取ることで解を求める．この手順は適応型であり，刻み幅は常に適当であるように自動調整される．値が特定の領域で急激に変化するときは，NDSolveが解を見逃さないように刻み幅が徐々に狭められるか，あるいはメソッドが変更される．

NDSolveの探索手順は適応型であるから，変数 の変化率が大きく異なるいくつかの要素を持つ，いわゆる「扱いにくい」微分方程式を解くこともできる．

NDSolveは，正確に解を追跡するまで刻み幅を減らすという一般的な手続きに従う．しかし，真の解に特異点がある場合，または積分区間が大きすぎる場合は問題がある．前者の場合は，NDSolveは指定された積分区間に対して意味をなすとみなす最小の刻み幅を制限する．後者の場合は，オプションMaxStepsを使って，NDSolveが解を見付けるために取ることのできるステップの最大数を指定する．常微分方程式では，デフォルトの設定はMaxStepsAutomaticである．Automatic設定では，NDSolveは初期の刻み幅に基づいて，問題の方程式を解くのに必要なステップ数を推定する．

解が滑らかなほとんどの関数では，MaxStepsのデフォルト値で十分間に合う．解が複雑な構造を取るようなときは，MaxStepsを大きく取っておくとよいだろう．また，MaxSteps->Infinityと設定しておくとステップの上限なしで探索ができる．

連立した微分方程式を解くとき，NDSolveではすべての方程式に適応するように刻み幅が自動調整される．しかし，場合によっては，NDSolveで最初に取るステップ幅が大きすぎて解の重要な特徴を見逃しかねない．このような問題を避けるには，オプションStartingStepSizeを使い第1ステップの幅を特別に指定しておく．

NDSolveに与える方程式すべてが導関数を含んでいる必要はない．単に代数的なだけでもよい．NDSolveを用いて多くの「微分代数方程式」を解くことができる．

FindRootと同様にFindMinimumとFindMaximumもある点から始めて次第に最小値または最大値を求める．しかしこれらの関数は何かが見付かり次第結果を返すので，大域的な値ではなく極小値あるいは極大値を返す可能性がある．

NMinimizeとNMaximizeは数値用のMinimizeとMaximizeと考えることができる．しかし，MinimizeやMaximizeとは異なり，大域的最小や最大を必ず見付けられるとは限らない．関数 f がある程度滑らかで極小と極大の数が限られていればこれらの関数はかなり効果がある．

目的関数 f と制約条件 cons の両方がすべての変数について線形の場合，最小化と最大化は「線形計画問題」に対応することになる．このような問題は明示的な方程式で記述するのではなく行列やベクトルで記述する方が便利なことがある．

リスト をペアの列の形にすると方程式と不等式の制約条件を混ぜて指定することができる． がなら 番目の制約条件は である．もし がなら制約条件は である．もし がならそれは である．

LinearProgramming[c,m,b,l]で を の上界と下界を表すペアのリストにすることができる．

大規模な線形計画法の問題を解く場合には行列 をSparseArrayオブジェクトとして与えると便利なことが多い．

NDSolveやNMinimizeのような数値操作を行う場合，Wolfram言語はデフォルトにより機械数を使う．しかし，オプションWorkingPrecision->n とすることで n 桁精度の任意精度数が使えるようになる．

WorkingPrecisionを設定すると，これは通常計算結果の精度の上限を定義する．しかし，この制約条件内でWolfram言語に目標精度と目標確度を指示することができる．多くの数値操作において目的精度と目的確度を数桁大きくするだけではるかに長い計算時間がかかるようになることは理解しておいた方がよい．それでもなお，高精度・高確度が確実に達成できることが重要な場合も多い．

WorkingPrecisionを特定の値に設定するときは，Wolfram言語における数値操作のための各関数がPrecisionGoalとAccuracyGoalに特定のデフォルト設定を使っていなければならない．その典型的な例はNDSolveである．そのデフォルト設定はWorkingPrecisionにおける設定値の半分になっている．

目標精度と目標確度の両方が返される最終結果とそれらのさまざまなノルムや誤差推定に適用される．Wolfram言語における数値操作の関数は通常指定の目標精度あるいは目標確度のどちらか一方に達した段階で結果を返す．どちらかの設定値がInfinityの場合はそうではない方だけが考慮される．

N[expr,n]で通常の数値評価を行う場合，Wolfram言語は結果が n 桁精度に達するように自動的に内部計算を調整する．しかし関数の数値操作を行う場合，実際にはWorkingPrecisionとPrecisionGoalをもっと明示的に指定する必要があるのが普通である．

Wolfram言語の関数は内部がどのような仕組みになっているのかを知る必要がないように注意深く設定されている．しかし，特に反復アルゴリズムを使用する数値計算の場合には，アルゴリズムの内部過程がモニターできると便利なことがある．

option->expr ではなく option:>expr を使うのが重要であることに注意されたい．expr が規則が与えられたときだけではなく，使われる度に評価されるためには遅延型の規則:>が必要である．

解へ向けて着実にステップを重ねるために，反復的な数値アルゴリズムが与えられた関数を数回評価しなければならないことがある．これは例えば各ステップが関数の値の差分によって導関数を推定しなければならないからだったり，ステップが成功するためにはいくつかの試みが必要だったりするからである．

特定のタイプの数値計算のため複数の異なるメソッドが知られていることがある．そのような場合にWolfram言語は普通文献で説明されているもの，説明されていないものの中で一般に最も成功率が高いものをサポートする．特定の問題に対し，最良のメソッドを自動的に選択するのには多大な努力が必要である．しかし，問題をよく知っていれば，あるいは数値メソッドについて研究しているのであれば，使うべきメソッドをWolfram言語に明示的に与えてみてもよいだろう．関数レファレンスページにはWolfram言語に組込まれているメソッドのいくつかが載っている．その他のメソッドについては「数値および関連関数」あるいは拡張ドキュメントで説明してある．

簡単な代数式で与えられる関数は，入力成分が少し変われば出力成分も少し変わる，という性質をよく持つ．しかし，実行手続型の関数には入力成分の変化に過剰に反応するような関数もある．これは，関数で使われる手続が入力の持つ有効数字を累進的に「削っていって」しまうからである．

FractionalPart[2x]の動作は，数 x のバイナリ表記における桁数を考えれば分かりやすい．最初の桁が落とされ，他の桁が左にシフトされる．この操作を何回か繰り返すと，より右寄りの桁に対して結果が敏感に反応してもおかしくない．右寄りの桁が x のもとの値にほとんど影響をおよぼさないのである．

特定の精度で入力すると，事実上桁数が限定されてしまう．1度，桁が「削られ」てしまうと正確な答は求まらない．精度を上げるためには，もとの入力の数字がもっと分かっていなけらばならないからである．任意精度の数を使っていれば，Wolfram言語は自動的にこのような精度の劣化を見張り，「任意精度の数」で説明してあるように，0.×10^e によって有効数字が残らないようにした数を示している．

どのような形の近似数でも，それを上記の例のように使うといずれ有効数字がなくなってしまう．任意精度の数を使えば，各ステップの精度が表示されるので少なくとも精度がどう悪化したかが確認できる．しかし，機械精度の数を使うと桁精度が管理できないため，求まった答が意味あるものかどうか分からなくなってしまう．

FractionalPart[2x]の操作を繰り返すたびに，直前の値から有効なバイナリ桁が抽出される．これらの桁の数字がランダム（例えば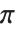， の桁）なら，答もそれに対応してランダムになる．一方，桁の数字が単純なパターンを持つ（例えば，有理数）と，答もそれに対応して単純な形を持つ．

FractionalPart[3/2x]のような操作を繰り返すと，はじめが単純な数であっても，ランダムな数の系列が求まってしまうことがある．この結果は，入力成分への過剰依存の話とは直接関係ないが，実はStephen Wolframが1980年代中頃に発見した極めて一般的な現象である．

反復処理を行う手続きに基づく関数は入力に対して過剰な依存性を示す．似たような状況が微分方程式の解にも言える．微分方程式の独立パラメータを変化させると，反復処理におけるあるステップから次のステップに移行するときの状況と同じことが起る．