函数中的数值运算

算术求数值根
Wolfram 语言中的数值数学微分方程数值解的介绍
数值数学的不定性微分方程的数值解
数值和、连乘与积分数值最优化
数值积分控制结果的精度
和与连乘的数值计算监控和选择算法
方程的数值解对输入敏感的函数
多项式方程的数值解
算术
用 Wolfram 语言做算术，如同在电子计算器上一样.
两数的和：
用 / 代表除，^ 代表幂：
在 Wolfram 语言中，空格表示乘号. 前端自动用浅灰的乘号符替换数字间的空格：
可以使用 * 表示乘号：
可以在算术表达式中使用括号：
x^y
幂
-x
负
x/y
除法
x y z
or
x*y*z
乘法
x+y+z
加法
Wolfram 语言的算术运算.
Wolfram 语言的算术运算根据标准数学的常规进行组合的. 例如，2^3+4 表示 (2^3)+4，而不是 2^(3+4). 您总能使用括号来明确地控制组合.
用科学记数法给出结果：
用科学记数法输入数：
或者这样：
在 Wolfram 语言中，您可以执行特殊精确度计算，通常高于普通计算器. 当给出确切的数字，Wolfram 语言不会转换为一个近似的代表数，其会提供精确的结果.
给出有理数：
给出近似数值解：
给出40位有效数字的近似数值结果：
Wolfram 语言中的数值数学
Wolfram 语言最重要的一个特征是给出精确的符号计算结果. 然而，有一些计算，其在数学上不能得到精确的“封闭形式”的结果，这时常常可以得到近似数值结果.
对于 没有“封闭形式”的结果. Wolfram 语言返回积分的符号形式：
现在去积分的符号形式，求数值值：
当 Wolfram 语言不能求出显式结果时，返回一个符号形式. 可以取这个符号形式，使用 N 求数值近似值.
给出 N 的第二个自变量，可以指定使用的数值精度：
如果想要在 Wolfram 语言中数值地计算积分，使用函数 Integrate 并且对结果应用 N 不是最有效的方法. 更好的方法是使用函数 NIntegrate，可以立即给出数值答案，不必先得到精确的符号结果. 应该认识到即使 Integrate 最后不再设法给出精确结果，可能已经花费了许多时间.
NIntegrate 直接计算数值积分，而不用得到符号形式：
IntegrateNIntegrate
定积分
SumNSum
求和
ProductNProduct
连乘
SolveNSolve
代数方程的解
DSolveNDSolve
微分方程的解
MaximizeNMaximize
最大化
Symbolic and numerical versions of some Wolfram Language functions.
数值数学的不定性
Wolfram 系统求数值积分的方法与求符号积分的方法完全不同.
求符号积分时，Wolfram 系统取被积函数的函数形式，对其使用一系列精确的符号变换规则来计算积分.
然而，当 Wolfram 系统求数值积分时，在一些初始符号预处理时候，其具有的被积函数的信息仅仅是被积函数的一系列数值值. 要得到积分的确切结果，Wolfram 系统必须对被积函数的光滑性和其他性质做出某种假定. 如果被积函数是严重病态的，这些假定可能失效，因此，Wolfram 系统可能对积分给出错误结果.
例如，当对在特定位置具有非常细的尖峰的函数进行数值积分时，这个问题可能出现. Wolfram 系统在许多点处对函数采样，然后假定函数在这些点间光滑变化. 因此，如果没有接近尖峰的采样点，那么尖峰将检测不到，对该数值积分的贡献就不能正确地包括进去.
函数 的图形：
NIntegrate 给出在区间 到 上的数值积分的正确结果：
然而如果在区间 到 上求此积分，NIntegrate 将丢失 附近的尖峰，而给出错误的结果：
NIntegrate 力图尽可能好地利用能得到的关于数值积分的信息. 例如，当 NIntegrate 注意到在某一区域中估计误差较大时，会在该区域取更多的采样点. 用这种方法，NIntegrate 尽量使运算适应特定的被积函数.
NIntegrate 使用的这种适应程序与函数 Plot 力图画出函数的光滑曲线所做的事情相类似. 在两种情况下，Wolfram 系统都是在特定区域中尽量取更多的采样点，直到在该区域找出函数的光滑近似为止.
出现在数值积分中的这种问题也会出现在函数的其他数值运算中.
例如，当求无穷级数和的数值近似时，Wolfram 系统在级数中取一定数量的项作为样本，然后用外插法估计其他项. 如果在级数中很后面的地方插入大的项，那么做外插时可能检测不到，这样可能得到错误的结果.
在求函数极小值的数值近似时，出现类似的问题. Wolfram 系统只采有限个样本值，然后在这些值之间对函数进行光滑插值. 如果函数在某区域有一个急剧的下降， Wolfram 系统可能错过这个下降，而给出错误的最小值.
仅对函数进行数值计算时，无法避免以上讨论的各种问题. 当然，如果进行精确的符号运算，可以避免这些问题.
在许多计算中，最好是尽量地使用符号运算，然后再引用数值方法，这样能最后地避免在纯数值计算中出现的问题.
数值和、连乘与积分
NSum[f,{i,imin,Infinity}]
的数值近似值
NProduct[f,{i,imin,Infinity}]
的数值近似值
NIntegrate[f,{x,xmin,xmax}]
的数值近似值
NIntegrate[f,{x,xmin,xmax},{y,ymin,ymax}]
重积分 的数值近似值
数值和、连乘与积分.
的数值近似值：
NIntegrate 能处理积分区间端点处的奇异性：
可以计算无穷区间上的数值积分：
三角形区域上的重积分. 注意积分变量给出的顺序：
更复杂的域上的重积分：
数值积分
N[Integrate[expr,{x,xmin,xmax}]]
尝试进行精确积分，然后求数值近似
NIntegrate[expr,{x,xmin,xmax}]
求积分的数值近似
NIntegrate[expr,{x,xmin,xmax},{y,ymin,ymax},…]
多重数值积分
NIntegrate[expr,{x,xmin,x1,x2,…,xmax}]
沿直线段求数值积分，从点 开始，经过点 ，到点 结束
数值积分函数.
求积分 的数值近似：
重积分 的数值近似：
NIntegrate 的重要特征是处理在已知点处“爆炸”的函数的能力. NIntegrate 自动地在积分区域的端点处检查这种问题.
函数 在 处爆炸，但 NIntegrate 仍然给出了正确的积分值：
Wolfram 语言能够求出 积分的精确值：
NIntegrate 检测到 在 处的奇异性，不是可积的：
NIntegrate 自动查找积分域端点和分段函数（如 Piecewise 和 Abs)定义的子区域的奇点. 当其他奇点存在时，NIntegrate 有可能给不出正确的积分结果. 然而，按照其自适应程序，NIntegrate 将常常检查奇点的存在，并给出有关的警告.
NIntegrate 给出关于积分域中间的奇点的一个警告. 最终结果很接近正确答案：
如果已知被积函数在某处有奇点，可以明确告诉 NIntegrate 来处理. NIntegrate[expr,{x,xmin,x1,x2,…,xmax}] 对 expr 从 xmin 到 xmax 积分，在中间点 xi 中查找奇点.
再一次给出积分，但此时明确处理 处的奇点：
在 NIntegrate 中可以使用中间点 xi 的列表来指定复平面上的路径. 路径由以 xmin 为起点，经过每一点 xi，以 xmax 为终点的若干线段组成.
在复平面的一条闭曲线上对 进行积分. 闭曲线从 开始，经过 ， 和 ，再回到 ：
上一积分的结果就是 ，正符合柯西定理：
选项名
默认值
MinRecursion0
积分区域的递归细分的最小数
MaxRecursionAutomatic
积分区域的递归细分的最大数
MaxPointsAutomatic
被积函数采样的最大次数
NIntegrate 的特殊选项.
当 NIntegrate 力图计算数值积分时，在一系列点上对被积函数采样. 当发现在一个特定区域内被积函数变化很快时，则在该区域递归地取更多的采样点. 参数 MinRecursion 和 MaxRecursion 指定递归细分层的最小和最大数. 增加 MinRecursion 的值保证 NIntegrate 使用较大的采样点数. MaxPoints 和 MaxRecursion 限制了NIntegrate 使用的采样点数. 增加 MinRecursion 或者 MaxRecursion 会使 NIntegrate 计算更慢.
在所有选项的缺省设置下，NIntegrate 丢失了 在 处的高峰，给出了错误的积分结果：
在选项设置 MinRecursion->3 下，NIntegrate 取足够多的采样点，使其注意到 附近的高峰. 然而在 MaxRecursion 的缺省设置下，NIntegrate 不能使用足够多的采样来得到精确结果：
在 MaxRecursion 的这个设置下，NIntegrate 能得到积分的精确结果：
解决此问题的另一方法是使用 NIntegrate 将积分区间分成若干段，其中一个小区间包含高峰：
多多重积分，NIntegrate 可能要花费很多时间得到结果. 然而，通过设置选项 MaxPoints，可以让 NIntegrate 给出较粗的估计，这时其仅对被积函数取限制次数的采样.
这是获取需较长计算时间的积分的粗略估计的方法：
和与连乘的数值计算
NSum[f,{i,imin,imax}]
求和 的数值近似
NSum[f,{i,imin,imaxdi}]
在和中使用步长
NProduct[f,{i,imin,imax}]
求连乘 的数值近似
数值和与连乘.
给出 的数值近似：
和没有精确结果，故 Wolfram 语言保留其符号形式：
可以明确使用 N 得到数值结果：
NSum 的工作方式是明确地包含确定的项数，然后尽量估计剩余项的值. 这三种攻击的方法，第一种使用欧拉-麦克劳林方法，通过积分计算余项. 第二个方法称为 Wynn epsilon 方法，在和中取更多项的采样，然后将其拟合成多项式乘以衰减的指数函数. 第三个方法，对于交错级数是很有用的，其采用交错符号的方法；对大量的剩余项进行采样，并且使用两个多项式的比率，求和的近似值（Padé 近似）.    
选项名
默认值
MethodAutomatic
Automatic，"EulerMaclaurin"， "WynnEpsilon"，或者 "AlternatingSigns"
NSumTerms15
明确包含的项数
VerifyConvergenceTrue
级数的收敛性是否应该被验证
NSum 的选项.
如果用户不明确指明使用的方法，NSum 将在 EulerMaclaurin 或者 WynnEpsilon 方法中进行选择. 在任何情况下，关于求和函数的一些假定必须给出. 如果假定不正确，可能得到不精确的结果.
使用 NSum 最常见的是计算无穷级数的和. 也可以用来计算有限级数的和. 通过对正在计算的对象做出隐含假定，NSum 常常可以避免像 Sum 计算所需的那么多函数计算.
通过外插求 的数值：
通过求和的符号形式，然后再进行数值计算也可得到该结果，尽管效率要低的多：
NProduct 的工作方式与 NSum 相同，也具有相应的选项.
方程的数值解
NSolve[lhs==rhs,x]
求多项式方程的数值解
NSolve[{lhs1==rhs1,lhs2==rhs2,…},{x,y,…}]
求多项式方程组的数值解
FindRoot[lhs==rhs,{x,x0}]
以 为初值的方程的一个数值解
FindRoot[{lhs1==rhs1,lhs2==rhs2,…},{{x,x0},{y,y0},…}]
求方程组的一个解
求数值根.
NSolve 给出多项式方程的全部根的数值近似值：
也可以使用 NSolve 求方程组的数值解：
如果方程中只包含线性函数或多项式，那么可以使用 NSolve 求出全部解的数值近似值. 但是，当方程中包含更复杂的函数时，一般求不出全部解. 甚至数值解也做不到. 在这种情况下，可以使用 FindRoot 求方程的一个数值解，此时，必须给出 FindRoot 进行搜索的初始值.
求方程的一个数值解，初始值为 ：
方程有多个解，当给定不同的初始值 时，FindRoot 求出不同的解：
求方程组的解，此处的解包含复数：
多项式方程的数值解
当 Solve 不能求出多项式方程的解时，用 Root 对象给出符号形式的结果：
使用 N 可得到数值解：
给出25位精度的数值解：
使用 NSolve 直接求多项式方程的数值解. 不必先求精确解：
NSolve[poly==0,x]
求多项式方程的数值近似解
NSolve[poly==0,x,n]
求 位精度的数值解
NSolve[{eqn1,eqn2,…},{var1,var2,…}]
求多项式方程组的解
多项式方程的数值解.
NSolve 可以对任意多项式方程或多项式方程组给出数值解的完全集合.
NSolve 可以求联立多项式方程组的解：
求数值根
NSolve 给出求多项式方程的数值近似值的一般方法. 然而，如 "一元方程" 中讨论的那样，对更一般的方程，求数值解将会困难的多. 函数 FindRoot 给出求任意方程或方程组的一个数值解的方法.
FindRoot[f,{x,x0}]
以 x=x0 为起点，求 f 的一个数值解
FindRoot[lhs==rhs,{x,x0}]
以 x=x0 为起点，求方程 lhs==rhs 的一个解
FindRoot[f1,f2,…,{{x,x0},{y,y0},…}]
求所有 fi 的一个联立数值解
FindRoot[{eqn1,eqn2,…},{{x,x0},{y,y0},…}]
求联立方程 eqni 的一个数值解
求数值根.
曲线 和 相交于一个点：
求交点 的数值近似. 0 告诉 FindRoot 关于 应该先尝试的起点：
在求方程的一个解中，FindRoot 从一个指定点开始依次尝试使得越来越接近一个解. 即使方程有多个解，FindRoot 总是返回其发现的第一个解，所求的是哪个解依赖于选择的起点. 只要起点充分靠近某个解，FindRoot 总是返回这个解.
函数 有无穷多个形如 的解. 如果起点靠近某个解，FindRoot 将给出该解：
如果起点为 ，得到的是 的近似值：
如果要使用 FindRoot 求复数解，必须给出复数起始值：
对 Riemann zeta 函数求解：
求解联立方程组：
FindRoot 所使用的变量可以具有形式为列表的值. 这使得用户可以求解以向量为自变量的函数的根.
对变量 求解线性方程的一种方法：
求解正则化的特征向量 和特征值 ：
微分方程数值解的介绍
NDSolve[eqns,y,{x,xmin,xmax}]
求微分方程中函数 y 的数值解，其中自变量 x 的变化范围从 xmin 到 xmax
NDSolve[eqns,{y1,y2,…},{x,xmin,xmax}]
求关于 yi 的微分方程组的数值解
微分方程的数值解.
这类求方程 在 上的数值解. 结果以插值函数InterpolatingFunction 的形式给出：
的值：
像 这样的代数方程，其 的解是一个数. 而微分方程的解是一个函数. 例如，对方程 ，用户想要得到的是函数 在自变量 的某区间上的近似值.
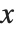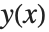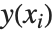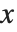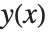Wolfram 语言把函数的数值近似值表示为 InterpolatingFunction 对象. 当给自变量 一个特定的值时，该对象返回 在该点处的近似值. InterpolatingFunction 存储着 的一个值表，然后对该值进行插值，求出在特定 处 的近似值.
y[x]/.solution
对函数 y 使用规则列表来得到 y[x] 的值
InterpolatingFunction[data][x]
计算插值函数在点 x 处的值
Plot[Evaluate[y[x]/.solution],{x,xmin,xmax}]
画微分方程的解曲线
使用 NDSolve 给出的结果.
求两个微分方程构成的方程组的解：
从解中求出的 z[2] 的值：
在线3上找到的 z[x] 的解的图形. 绘图函数 Plot 将在 "基本画图 " 中讨论：
NDSolve[eqn,u,{x,xmin,xmax},{t,tmin,tmax},…]
求解偏微分方程
偏微分方程的数值解.
微分方程的数值解
"微分方程数值解的介绍" 中讨论的函数 NDSolve 可用以求微分方程的数值解. NDSolve 既可处理单个微分方程，又可处理联立微分方程组. 其可以处理范围很广的常微分方程以及某些偏微分方程. 在一个常微分方程系统中，可能有任意个未知函数 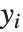，但这些函数都必须依赖于单个“独立变量” 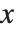. 偏微分方程则包含两个或更多的独立变量. NDSolve 也可以处理混合了微分方程和代数方程的微分代数方程.
NDSolve[{eqn1,eqn2,…},y,{x,xmin,xmax}]
求在 x 的区间 xmin 到 xmax 上，函数 y 的数值解
NDSolve[{eqn1,eqn2,…},{y1,y2,…},{x,xmin,xmax}]
求多个函数 yi 的数值解
求常微分方程的数值解.
NDSolve 将函数 yi 的解表示为 InterpolatingFunction 对象. 这种 InterpolatingFunction 对象提供独立变量 x 从 xmin 到 xmax 上的 yi 的近似值.
NDSolve 用迭代法求解. 从某个 x 值开始，然后进行一系列的步进，最终覆盖从 xmin 到 xmax 的整个区域.
要进行计算，必须对 NDSolve 给定 yi 和其导数的适当的初始或边界条件. 这种条件指定在某个点 x 处的函数值 yi[x] 或者导数值 yi'[x]. 一般可以在任何点 x 处给定条件，至少对常微分方程如此，NDSolve 将自动覆盖区域 xmin 到 xmax.
求在 x 的区间 0 到 2 上， y 的数值解，初始条件为 y[0]：
仍然求在 x 的区间 0 到 2 上的数值解，但是现在的初始条件为 y[3]：
一个简单的边值问题：
使用 NDSolve 时，给定的初始或者边界条件必须能完全确定 yi 的解. 在使用 DSolve 求微分方程的符号解时，可以指定较少的初始条件. 这是因为 DSolve 自动地插入任意常数 C[i] 来表示相应于未明确指定的初始条件的自由度. 由于NDSolve 必须给出数值解，其不能表示这种附加的自由度. 因此，必须明确指出确定解所需的全部初始和边界条件.
一个典型的情形是 阶微分方程需要给出直到 阶导数的初始条件，或给出在 个点处的边界条件.
对于三阶方程，需要给出直到二阶的初始条件：
画出所得解的图形：
对于三阶方程，也可以给出在三个点处的边界条件：
Wolfram 语言允许使用函数和导数值的适当的线性组合作为边界条件：
在大多数情况下，给出的初始条件必须包含相同的 x 值，例如 x0. 因此，可以不必明确给出 xmin 和 xmax 两个值. 当指定 x 的区域为 {x,x1} 时，Wolfram 语言将自动生成 x0 到 x1 的区域上的解.
生成0到2上的解：
可以用方程形式给定初始条件. 这些方程可能有多个解. 在这种情况下，NDSolve 相应地生成多个解.
此例中的初始条件导致多个解：
所有解的图形：
可以使用 NDSolve 求解耦合微分方程系统的解.
求一对耦合方程的数值解：
画出上述解 y 的图形：
使用上述解的 x 和 y 产生一个参数方程的图形：
微分方程中的未知函数不是必须用单个符号来表示. 当未知函数的数目很多时，把他们命名为 y[i] 将是更方便的.
这里构造5个耦合微分方程的方程组及初始条件：
求解上述方程组：
解的图形：
NDSolve 可以处理值为列表或数组的函数. 如果给出类似 y[0]=={v1,v2,…,vn} 的初始条件，那么 NDSolve 将假定 y 是值为长度为 n 的列表的函数.
求解4个耦合微分方程的方程组：
解的图形：
选项名
默认值
MaxStepsAutomatic
对 采取的最大步数
StartingStepSizeAutomatic
所用的初始步长
MaxStepSizeAutomatic
所用的最大步长
NormFunctionAutomatic
用于误差估计的范数
NDSolve 选择.
NDSolve 有许多方法来求解方程，但是基本上所有的方法都是通过取独立变量 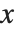的一系列步进来工作，并且使用自适应程序来决定步长的大小. 一般，如果解在某个区域中变化得很快，那么 NDSolve 将减小步长以便更好地跟踪解.
求解的微分方程中，导数有一个不连续点：
NDSolve 在 附近取较小的步长，以便准确地产生转折点：
通过自适应程序，NDSolve 能求解具有若干个 变化速率差别很大的分量的微分方程.
在这些方程中，y 变化得比 z 快得多：
NDSolve 成功地跟踪了这两个分量：
NDSolve 遵循这样的一般过程：减小步长的大小直到精确地跟踪解. 然而，当真解有奇点或积分间隔太大时时，会出现问题. 对于第一种情形，NDSolve 会限制最小步长，这对于给定积分间隔是有意义的. 对于第二种情形，选项 MaxSteps 指定 NDSolve 求解采取的最大步数. 对常微分方程，缺省设置是 MaxStepsAutomatic. 使用 Automatic 设置，NDSolve 会基于初始步长估计求解方程所需的步数.
当步长太小时，NDSolve 会停止：
该解在 处有一个奇点：
MaxSteps 的缺省对于大多数具有光滑解的方程来说已足够了. 然而，当解有复杂的结构时，可能必须选择更大的MaxSteps 的值. 当设置为 MaxSteps->Infinity 时，使用的步数没有上限.
对罗伦兹方程要产生解的完整结构，需要给出 MaxSteps 的更大设置：
上述解的三维图形：
当 NDSolve 求解特定微分方程组时，总是尽量选择适合这些方程的步长. 在有些情况下，NDSolve 采取的第一步的步长可能太大，这样可能丢失解的重要特征. 要避免这个问题，可以明确地设置选项 StartingStepSize 来指定第一步的步长.
对于 NDSolve 给出的方程不必全部涉及导数；他们也可以就是代数形式的. 用户可以使用 NDSolve 来求救许多这种类型的微分代数方程.
求解微分代数方程：
解的图形：
NDSolve[{eqn1,eqn2,…},u,{t,tmin,tmax},{x,xmin,xmax},…]
求偏微分方程的解 u
NDSolve[{eqn1,eqn2,…},{u1,u2,…},{t,tmin,tmax},{x,xmin,xmax},…]
求偏微分方程组的解 ui
求偏微分方程的数值解.
求波动方程的数值解. 结果是二维插值函数：
生成上述结果的图形：
求非线性波动方程的数值解：
生成上述结果的三维图形：
解的高分辨率的密度图：
方程在2+1维的版本：
求解方程：
生成解的图形列表：
数值最优化
FindMinimum[f,{x,x0}]
以 x=x0 为初始点，搜索函数 f 的局部极小值
FindMinimum[f,x]
搜索函数 f 的局部极小值
FindMinimum[f,{{x,x0},{y,y0},…}]
搜索多变量函数的局部极小值
FindMinimum[{f,cons},{{x,x0},{y,y0},…}]
以 x=x0, y=y0, … 为初始点，搜索在约束条件 cons 下的局部极小值
FindMinimum[{f,cons},{x,y,…}]
在约束条件 cons 下搜索局部极小值
FindMaximum[f,x]
, etc.
搜索局部极大值
搜索局部极小值和极大值.
求使 达到极小的 的值，起始点为 ：
列表的最后一个元素给出获得极小值对应的变量值：
与 FindRoot 一样，FindMinimum 和 FindMaximum 从一个点开始，循序渐近地寻找极小值或极大值. 但是由于他们一旦找到一个极值，就会返回结果，可能只给出函数的局部极小值或极大值，而不是全局的极小值或极大值.
该曲线具有两个局部极小值：
以 为初始点时，在右边获得局部极小值：
以下情况给出左边的局部极小值，在本利中也是全局极小值：
指定变量时可以不使用初始值：
用户可以指定一个约束条件：
NMinimize[f,x]
尝试求 f 的全局极小值
NMinimize[f,{x,y,…}]
尝试求多变量函数的全局极小值
NMaximize[f,x]
尝试求 f 的全局极大值
NMaximize[f,{x,y,…}]
尝试求多变量函数的全局极大值
求全局极小值和极大值.
立即找到全局极小值：
NMinimize 和 NMaximize 是 Minimize 和 Maximize 的数值模拟. 但是与 Minimize 和 Maximize 不同，他们经常不能保证可以找到绝对的全局极小值和极大值. 然而，当函数 f 很平滑，并且具有有限数目的局部极小值和极大值的时候，通常表现良好.
NMinimize[{f,cons},{x,y,…}]
尝试在约束条件 cons 下求 f 的全局极小值
NMaximize[{f,cons},{x,y,…}]
尝试在约束条件 cons 下求 f 的全局极大值
在约束条件下，求全局极小值和极大值.
在约束条件 下，NMinimize 将给出右边的局部极小值：
求在单位圆内 的极小值：
对这个例子，Minimize 可以给出精确结果：
但是以下情况就不可以：
给出一个数值近似，实际上是使用了 NMinimize：
如果目标函数 f 和约束条件 cons 对于所有变量都是线性的，那么极小化和极大化就对应于一个线性规划问题. 有时候，用矩阵和向量的形式代替明确的方程组来描述这些问题更为方便.
LinearProgramming[c,m,b]
求在约束条件 和 下极小化 的向量
LinearProgramming[c,m,b,l]
使用约束条件 和
线性规划的矩阵形式.
以方程形式给出的线性规划问题：
相应问题的矩阵形式：
可以把列表 写成一个数字对 的序列来指明等式和不等式混合约束条件. 如果 为 ，那么第 个约束条件为 . 如果 为 ， 那么约束条件为 ，如果 为，那么约束条件为 .
第一个不等式用 ：
在 LinearProgramming[c,m,b,l] 中，可以把 写成形如 的数字对列表，分别表示 的上界和下界.
在实现大型线性规划问题时，把矩阵 作为 SparseArray 对象给出常常是方便的.
控制结果的精度
在进行数值操作如 NDSolve 和 NMinimize 时，Wolfram 语言默认地使用机器精度数. 但是通过设置选项 WorkingPrecision->n 用户可以使用任意 n 位精度的数字.
进行数值积分的机器精度数的计算：
进行使用30位任意精度数进行计算：
如果用户对 WorkingPrecision 给出设置，这就通常定义了计算所得结果的精度的上限. 但是在这个约束条件下，用户可以告诉 Wolfram 语言自己想要达到的精度和准确度为多少. 用户应该意识到对于许多不同种的数值操作，如果只对精度目标和准确度目标增加小数目的数位，通常会大幅度地增加计算时间. 然而，在许多情况下，确保获得高精度和准确度是很重要的.
WorkingPrecision
内部计算中保持的精度位数
PrecisionGoal
尝试获得的精度的位数
AccuracyGoal
尝试获得的准确度的位数
控制精度和准确度的选项.
给出具有25位精度的结果：
使用30位工作精度不能达到50位精度：
给定 WorkingPrecision 的特殊设置，在 Wolfram 语言中数值操作的每个函数对 PrecisionGoal 和 AccuracyGoal 使用某种默认设置. 典型情况是 NDSolve，其中这些默认设置相当于对 WorkingPrecision 给定的设置的一半大小.
精度和准确度目标通常可以应用于返回的最终结果和关于其不同范数或误差估计. 在 Wolfram 语言中数值操作的函数通常不断尝试修订结果，直到达到指定的精度目标或准确度目标为止. 如果这两个目标之一设置为 Infinity，那么只考虑另一个目标.
在使用 N[expr,n] 进行普通数值计算时，Wolfram 语言自动调整内部计算以在结果中达到 n 位精度. 但是在对函数进行数值操作时，实际上经常需要更加明确地指明 WorkingPrecision 和 PrecisionGoal.
监控和选择算法
在 Wolfram 语言中函数被仔细地创建，因此用户通常不知道这些函数内部如何运作. 但是特别地，对于使用迭代算法的数值函数来说，有时候能够监控这些算法的内部运行进展是很有用的.
StepMonitor
当采取一个成功的步进时，所计算的表达式
EvaluationMonitor
当输入的函数被计算时，所计算的表达式
当输入的函数被计算时，所计算的表达式
显示每采取一个步进的时候，所对应的 x 值：
注意到使用 option:>expr 而不是 option->expr 是很重要的. 用户需要延时规则 :> 以使 expr 在每次使用而不是在给出规则的时候计算.
Reap 和 Sow 提供了方便的方式来对采取的步进生成列表：
计算步进数目：
要对一个答案采取成功的步进，有时候迭代数值算法必须对给定的函数做一些计算. 有时候，这是因为每个步进的需要，例如，从函数值的差异估计导数，并且有时候这是因为要采取一个成功的步进需要做多次尝试.
显示在获得答案的时候所采取的成功的步进：
当函数每次计算时都进行显示：
在 Wolfram 语言中算法实现的计算模式可以相当复杂：
Method->Automatic
自动地选择方法（默认）
Method->"name"
指定要使用的明确方法
Method->{"name",{"par1"->val1,…}}
指定方法的更多详细信息
Method 选项.
对于特定类型的数值计算，经常有一些已知的不同方法. 通常 Wolfram 语言支持在已有文献中被最广泛使用的成功算法，以及那些没有广泛被使用的算法. 对于任何特定问题，通常以相当大的努力自动挑选最好的方法. 但是如果用户对一个问题掌握了丰富的知识，或者用户正在研究符合自身利益的数值方法，用户可能会发现明确告诉 Wolfram 语言应该使用什么方法是有益的. 函数参考页面列出了 Wolfram 语言内置的一些方法；其他函数在 "数值及相关函数" 中或其他高等文档中进行讨论.
使用方法 求解微分方程，并且返回步进数目和所需计算数目：
通过自动选择的方法，得到了所需的步进和计算数目：
表明使用其他一些可能的方法会发生的情况. 自动选中的 Adams 方法是最快的：
表明当差分阶数的参数改变时，使用明确 Runge–Kutta方法会发生什么情况：
对输入敏感的函数
由简单代数公式表示的函数在其输入有微小的改变时，输出也仅有微小改变. 但对建立在执行程序上的函数，常常表现出对输入几乎任意的敏感依赖. 这种现象发生的主要原因是程序“挖掘”输入的有效数字变得越来越少.
依次显示输入为 0.1111 下的简单循环过程中的每一步：
输入为 0.1112 下的结果. 可以看到与输入 0.1111 下结果的累进差别：
FractionalPart[2x] 根据数 x 的二进制数位进行计算，其做法特别简单：删去第一位，将剩余的位向左移. 经过几步以后得到的结果不可避免地对远离右边的数据位是敏感的，对最初的 x 值有很小的影响.
显示从 FractionalPart[2x] 获得的 x 的前8个二进制位的移动过程：
以一个特定精度给出输入时，也就是仅指定了一定的位数. 一旦所有的位数被“”完，就不再能得到精确结果，因为这需要知道原始输入的更多位数. 只要使用任意精度数，Wolfram 语言将自动地保持跟踪这种精度的退化，这表明了在 0.×10e 上没有剩余有效数位的数，正如 "任意精度的数" 中所述.
依次的各步产生累进精度更低的数，最终没有留下任何精度：
询问每个数的精度. 零精度表明没有正确的有效数位：
显示出结果是周期序列：
如果使用任何类型的近似数，那么在类似于上述的例子中，最后总是用完精度. 但是，只要使用任意精度数， Wolfram 语言将明确显示所出现的精度降低. 而使用机器精度数，Wolfram 语言将不保持精度的跟踪，这样用户将无法辨别什么时候结果变得没有意义.
如果使用机器精度数，Wolfram 语言将不再保持对精度降低的跟踪：
重复计算 FractionalPart[2x]，将依次提取所给出的数的二进制数位. 如果这些数位明显是随机的——如 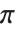中的数位——那么结果将相应是随机的. 但是如果数位有简单类型——如有理数——那么得到的结果将相应是简单的.
然而通过重复计算 FractionalPart[3/2x]，即使对非常简单的输入也可能得到看起来是随机的序列. 这是一个非常一般的现象的例子，是作者 Stephen Wolfram 在1980年代的中期首先确立的，其与输入的敏感依赖性没有直接关系.
生成看起来是随机的序列，即使从简单的输入开始：
在值被计算出来以后，可以安全地求出其数值近似：
重复1000次后的最后5个结果，计算中使用精确数：
使用机器精度数得到完全不正确的结果：
许多种循环过程产生敏感依赖于输入的函数. 这样的函数也出现在查看微分方程的解中. 实际上，改变微分方程的独立参数是在循环过程中从一步到下一步的连续模拟.
以下使用初始条件1求 Duffing 方程的解：
显示解的图形：
使用初始条件 1.001 的相同方程：
这个解逐渐地偏离上一个解：