級数,極限,留数
| Sum[f,{i,imin,imax}] | 和 |
| Sum[f,{i,imin,imax,di}] | di 刻みで i を増加させた和 |
| Sum[f,{i,imin,imax},{j,jmin,jmax}] | 重和 |
| Product[f,{i,imin,imax}] | 乗積 |
Wolfram言語には重和と重積に対応した記述法もある.i と j 上の二重和は,Sum[f,{i,imin,imax},{j,jmin,jmax}]と記述する.これは,慣用的な数学表記の  に対応している.なお,Wolfram言語の記述では,数学表記と同様に最も外側にある変数が最初に指定されることに注意してほしい.
に対応している.なお,Wolfram言語の記述では,数学表記と同様に最も外側にある変数が最初に指定されることに注意してほしい.
SumとProductにおける変数の範囲の指定の仕方は,Wolfram言語全体で標準の「反復子の記述法」に従っている.この記述法は,Tableを使ったリストの作成(「数値の表を作る」)とDoループの構築(「反復処理」)を説明する際に再び登場する.
| {imax} | 反復処理を imax 回行う(刻みに関する指定はなし) |
| {i,imax} | i を1〜imax の間で1刻みで増分 |
| {i,imin,imax} | i を imin〜imax で1刻みで増分 |
| {i,imin,imax,di} | i を imin〜imax で di 刻みで増分 |
| {i,imin,imax},{j,jmin,jmax},… | i を imin〜imax で1刻みで増分させ,各々の値において j を jmin〜jmax で増分 |
未知の関数が与えられると,Seriesは微分係数を使いベキ級数展開する:
ベキ級数は,近似値が数値計算に対して持つ役割と同じような働き方を代数式に対して行う近似式である.Wolfram言語を使い,ベキ級数に対して演算操作を行うことができる.その際に結果として求まるベキ級数には,適切な位数,もしくは「精度次数」が常に保持される.
Expandを答に適用させると11個の項からなる結果が求まる:
| Series[expr,{x,x0,n}] | expr について x=x0 近傍で最高 (x-x0)n 次までベキ級数展開を行う |
| Series[expr,{x,x0,nx},{y,y0,ny}] | |
最初 y について,次に x についてベキ級数展開を行う | |
Seriesの機能は数学的にいって,関数についてテイラー(Taylor)級数を構成することにある.
さらに,Seriesを使うと,標準的なテイラー級数の公式で直接カバーされない分数や負の指数部分を持つベキ級数も展開できる.
Seriesを使えば,対数項を持つ級数でも展開できる:
特に負のベキが現れるとき,Seriesが実際にいくつ項を生成するかで微妙な問題が生じる.
特定の次数まで取ったベキ級数と特定の精度で取った実数とを比較し類推してみると,このとき展開がどう進むか理解しやすくなる.すなわち,有限精度の実数を近似値とみなすようにベキ級数は「近似式」とみなされる.
ベキ級数を構築するためにSeriesで取られる手順は,ちょうどNにおいて実数の近似値を求めるために使われる手順によく似ている.つまり,これらの関数ではともに,展開する式が,最小な部分から有限の次数に(または,有限の桁精度に)置換され,そうすることで近似された式が評価される,という手順が取られる.例えば,項の相殺等が起ると,この手順だと指定した次数や桁精度に達しないところで展開が打ち切られる状況も起り得る.ただし,Nと異なりSeriesには,指定した次数の展開が得られるまでなるべく計算を繰り返す機能を持たせてあるので,仮に指定した次数まで展開し切れなくても,高い次数を指定しておけば十分に高い精度の展開が可能である.
変数 x についてベキ級数展開をするとき,関数が具体的に x を含まないと,同オブジェクトは x から独立しているものとみなされる.このため,Seriesの構築するテイラー級数は,実はDの機能をもとに偏微分を取ることで展開が行われる.
Wolframシステムにおけるベキ級数は,SeriesDataオブジェクトとして表される.
求まるベキ級数は項の和として出力される.最後の項O[x]はベキ乗としてある:
入力表記にしてみると,展開式が内部的にはSeriesDataオブジェクトとして扱われているのが分かる:
Wolframシステムにおいてベキ級数は通常の式の形ではなく,SeriesDataオブジェクトとして表される.そうすることで,次数や展開点がどうなっているか記録が簡単になり,ベキ級数に演算をする際に速やかに対処できる.ただし,普通に使っている限りユーザがSeriesDataオブジェクトの内部構造を知る必要はないだろう.
標準表記を出力形式に使っているとき,式がベキ級数かどうかを判別するには,O[x]項があるかどうかを確認することでできる.この項は数学の表記で一般的に使われる 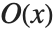 に相当するもので,無視された高次の
に相当するもので,無視された高次の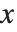 項を表すのに使われる.記述上の一貫性を保つため,Wolframシステムでは無視された
項を表すのに使われる.記述上の一貫性を保つため,Wolframシステムでは無視された 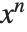 次の項の代りにO[x]^n が使われ,これは数学で使う
次の項の代りにO[x]^n が使われ,これは数学で使う 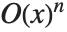 の記述に対応している.より一般的な
の記述に対応している.より一般的な 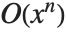 ではないことに注意する.
ではないことに注意する.
入力した和の式にO[x]の項があると即座にベキ級数の形に変換される.
O[x]が式にあるので,この和の式はベキ級数に変換される:
対数因子はSeriesData係数リストの中に明示的に現れる:
有限精度実数が的確な桁数になっているか常に検査され自動調整されるように,ベキ級数の次数精度もまた自動調整される.数値計算の場合と同じように,ベキ級数の演算でも演算操作によっては次数精度が上がったり下がったりする.
| ComposeSeries[series1,series2,…] | ベキ級数を合成 |
| InverseSeries[series,x] | ベキ級数の逆関数を取る |
方程式  を
を 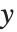 について解くとき,関数
について解くとき,関数 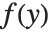 についてベキ級数が存在するのであれば,この級数を使った近似解を得ることが可能になることがよくある.このベキ級数は結局,
についてベキ級数が存在するのであれば,この級数を使った近似解を得ることが可能になることがよくある.このベキ級数は結局,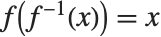 となる逆関数
となる逆関数 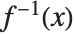 を与えていることになる.逆関数に関するベキ級数を求めることをベキ級数の復帰ともいう.
を与えていることになる.逆関数に関するベキ級数を求めることをベキ級数の復帰ともいう.
| Normal[expr] | ベキ級数を通常の式の形に変換する |
Normalを作用させ式に変換する.求まる式は高次の項が省略されたものである:
| SeriesCoefficient[series,n] | ベキ級数から n 次項の係数を抽出する |
| LogicalExpand[series1==series2] | ベキ級数から各々対応した係数を抽出し,等しいとすることで方程式を構築する |
| Solve[series1==series2,{a1,a2,…}] | 係数についてベキ級数の方程式を解く |
| Sum[expr,{n,nmin,nmax}] | n が nmin から nmaxまでの式 expr の総和を計算する |
数学の公式集にある和の式ならWolframシステムですべて求まる.不定積分でそうだったように,単純な関数を含む式からなる不定和でも,その答は複雑なものになりがちである.それでも,定積分のように,定形の和については,求まる答がもとの関数より簡単な関数で構成することが可能である.
| RSolve[eqn,a[n],n] | 再帰方程式を解く |
RSolveは a[n]に線形にだけ依存するのではない方程式を解くことができる.しかし,非線形方程式の場合は複数の異なる解が与えられなければならないこともある.微分方程式の場合と同じように,再帰方程式の記号解を求めるのは難しく,標準的な数学関数は限られたケースしか扱わない.
| RSolve[{eqn1,eqn2,…},{a1[n],a2[n],…},n] | |
再帰方程式の対になった系を解く | |
| RSolve[eqns,a[n1,n2,…],{n1,n2,…}] | |
偏再帰方程式を解く | |
複数の変数を持つ関数を含む偏微分方程式が設定できるように,多次元の文字列を含む偏再帰方程式を設定することもできる.微分方程式におけるのと同じように,偏再帰方程式の一般解は未定義の関数を含むことができる.
| Limit[expr,x->x0] | 式 expr の x が x0に接近していったときの極限を求める |
ある点についてすべての関数が極限を持っているとは限らない.例えば,関数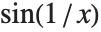 は
は  の近傍で激しく振動するため,定まった極限を持たない.とはいうものの,
の近傍で激しく振動するため,定まった極限を持たない.とはいうものの,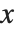 が実数である限り
が実数である限り  の近傍における関数の値は必ず
の近傍における関数の値は必ず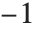 から
から の範囲にある.極限がある有限の幅の中を動くとき,LimitはIntervalを使ってその区間を示す.Interval[{xmin,xmax}]は,不確定な極限の値が
の範囲にある.極限がある有限の幅の中を動くとき,LimitはIntervalを使ってその区間を示す.Interval[{xmin,xmax}]は,不確定な極限の値が  から
から  の間にあることを示す.
の間にあることを示す.
Intervalオブジェクトには演算操作が行える:
Intervalオブジェクトが使われ極限がシンボル的に表される:
| Limit[expr,x->x0,Direction->1] | x が x0に下から接近したときの極限を求める |
| Limit[expr,x->x0,Direction->-1] | x が x0 に上から接近したときの極限を求める |
Limit[expr,x->x0] とすると,x が x0 に接近したときの式 expr の値が求められる.この値が無限大になる場合,x が x0 のときの expr の留数を求めた方が便利なことがよくある.留数は,expr を点 x0 でベキ級数展開したときに得られる 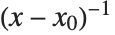 の項の係数で与えられる.
の項の係数で与えられる.
| Residue[expr,{x,x0}] | x が x0 のときの式 expr の留数を求める |
パデ近似はテーラー多項式を一般化したものと考えられる有理関数である.有理関数は多項式の比である.有理関数には基礎演算しか使われないので,数値的評価が非常に簡単である.分母多項式を使うと,有理特異点を持つ関数を近似することができる.
| PadeApproximant[f,{x,x0,{n,m}}] | 中心 x0で次数(n,m)の |
| PadeApproximant[f,{x,x0,n}] | 中心 x0で次数 n の |
より正確に言うと,正則点あるいは極 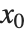 における次数
における次数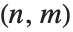 の解析関数
の解析関数 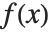 のパデ近似は有理関数
のパデ近似は有理関数 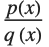 である.ここで
である.ここで 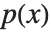 は次数
は次数 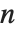 の多項式,
の多項式,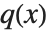 は次数
は次数 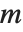 の多項式であり,点
の多項式であり,点 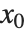 付近の
付近の  の形式的ベキ級数は項
の形式的ベキ級数は項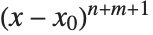 から始まる.もし
から始まる.もし 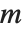 が
が 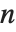 に等しければ,近似は次数
に等しければ,近似は次数 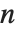 の対角パデ近似と呼ばれる.
の対角パデ近似と呼ばれる.
Wolfram言語では,PadeApproximantは分岐点付近での展開を許すよう一般化されている.