DOCUMENTATION CENTER SEARCH
Mathematica
>
Algebraic Number Theory
>
Built-in
Mathematica
Symbol
Algebraic Number Fields
Tutorials »
|
AlgebraicNumberNorm
MinimalPolynomial
SymmetricPolynomial
NumberFieldDiscriminant
See Also »
|
Algebraic Number Theory
More About »
AlgebraicNumberTrace
AlgebraicNumberTrace
[
a
]
gives the trace of the algebraic number
a
.
MORE INFORMATION
The trace of
a
is defined to be the sum of the roots of its minimal polynomial.
AlgebraicNumberTrace
[
a
,
Extension
→
]
finds the trace of
a
over the field
.
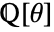EXAMPLES
CLOSE ALL
Basic Examples
(1)
In[1]:=
Out[1]=
In[2]:=
Out[2]=
Scope
(4)
Options
(1)
Properties & Relations
(3)
SEE ALSO
AlgebraicNumberNorm
MinimalPolynomial
SymmetricPolynomial
NumberFieldDiscriminant
TUTORIALS
Algebraic Number Fields
MORE ABOUT
Algebraic Number Theory
New in 6
© 2008 Wolfram Research, Inc.
] finds the trace of a over the field ![Q[theta]](Files/AlgebraicNumberTrace.en/3.gif "Q[theta]"){kind=small}
.
EXAMPLES
Basic Examples 
Scope 