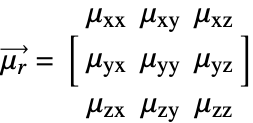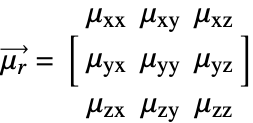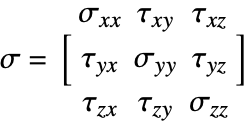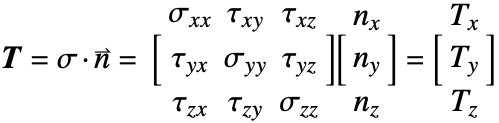Magnetostatics for Permanent Magnets
| Contents | Convergence of Magnetostatics Models |
| Introduction | Boundary Conditions |
| Overview Example | Conditions at Material Interfaces |
| Equations | Nomenclature |
| Secondary Quantities | References |
Contents
Introduction
This monograph uses partial differential equations to model and analyze time-independent magnetic fields, which are produced by permanent magnets. In the static regime, the electric and magnetic fields are not coupled, which means that when simulating magnetostatic fields, effects such as induced currents do not exist. See the Electromagnetics Overview for more information.
In this monograph, magnetostatic fields are simulated using the scalar magnetic potential formulation. This formulation is derived from the time-independent Maxwell's equations in combination with constitutive relations that describe the interaction of the magnetic fields with matter. In this formulation, the variable to solve for is the scalar magnetic potential ![]() .
.
The scalar magnetic potential formulation is used exclusively to model permanent magnets and given by:
where ![]() is the scalar magnetic potential in units of [
is the scalar magnetic potential in units of [![]() ],
], ![]() is the vacuum permeability in units of [
is the vacuum permeability in units of [![]() ], and
], and ![]() is the magnetization vector in units of [
is the magnetization vector in units of [![]() ]. In this formulation, there are no currents.
]. In this formulation, there are no currents.
Modeling electromagnetic devices with partial differential equations (PDEs) is not the only way to model electromagnetic devices. Other techniques include, for example, setting up ordinary differential equations (ODEs). This approach is followed by the Wolfram System Modeler. Roughly speaking, the system modeler approach is more suitable for large systems of electromagnetic devices interacting, while the partial differential equation approach is more suitable for a fine-grained analysis of a specific device. In some cases, it is beneficial to use a combination of the two approaches.
The approach taken in the introductory section is that a permanent magnet is used to introduce a magnetostatic analysis and show the functionality available. This will be followed by a more theoretical explanation of the underlying ideas and concepts. The theoretical background is much easier to understand once an intuition for the magnetostatic current-free analysis exists. After that, the available boundary conditions are discussed.
The goal of a magnetostatic analysis is to find the scalar potential distribution ![]() under specific constraints. A subsequent step then finds secondary fields, such as the magnetic flux density
under specific constraints. A subsequent step then finds secondary fields, such as the magnetic flux density ![]() [
[![]() ]. The analysis and interpretation of these physical quantities are useful to create a better quality engineering design of the device under consideration.
]. The analysis and interpretation of these physical quantities are useful to create a better quality engineering design of the device under consideration.
The modeling process as such results in a system of partial differential equations (PDEs) that can be solved with NDSolve. Extended examples of electromagnetic modeling can be found in the Model Collection.
The electromagnetic device analysis is typically done in stages. First, for the object to be analyzed, a geometric model needs to be created. The geometric model is typically created within a computer-aided design (CAD) process. CAD models can either be imported or created in product. To import geometries, common file formats like DXF, STL or STEP are supported. These geometries can be imported with Import. The alternative is to create the geometrical models in product, for example, by using OpenCascadeLink.
Once the geometric model is made available, some thought needs to be put into what type of analysis is to be performed. The next step is then the setup of boundary conditions and constraints. Materials to be used further specify the PDE model. Once the PDE model is fully specified, the subsequent finite element analysis will then compute the desired quantities of the device under investigation. These quantities are then post-processed, either by visualizing them or by computing derived quantities. This tutorial shows the necessary steps for everything except the CAD model generation.
Electromagnetic devices are typically three-dimensional objects. For the models, special cases exist that result in simplified 2D models. In fact, 2D models have been known to solve 90% of the important problems in electrical engineering [Cardoso, 2018]. 2D models are advantageous, as they are often easier to set up and need less computer time and memory to solve.
The symbols and corresponding units used throughout this tutorial are summarized in the Nomenclature section.
Overview Example
To illustrate the usage of the finite element method in electromagnetics, it is instructive to present a simple example and give an overview of the setup, various analyses and post-processing steps possible.
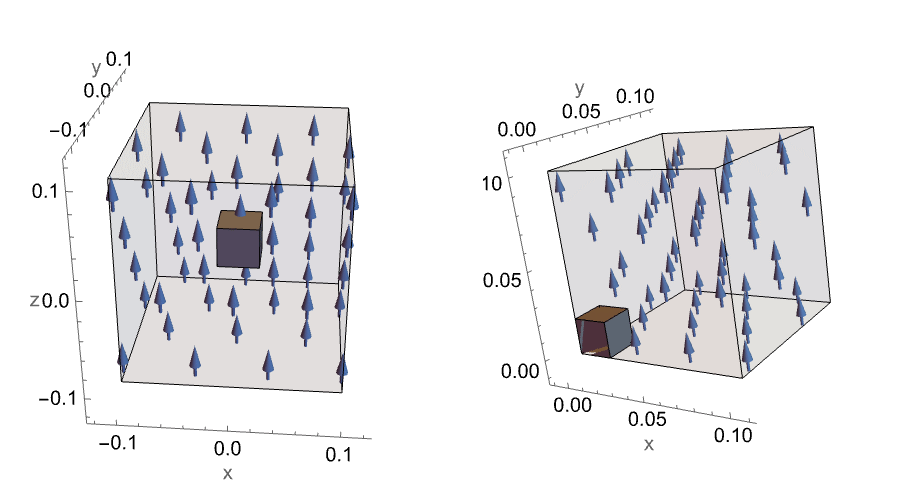
In this overview example, the workflow of setting up a magnetostatic PDE model is introduced. To keep things simple, a 3D cylindrical permanent magnet is modeled. The cylinder magnet is of height ![]() [
[![]() ] and radius
] and radius ![]() [
[![]() ]. Also, a sphere of air of radius
]. Also, a sphere of air of radius ![]() [
[![]() ] is created that represents the surrounding volume.
] is created that represents the surrounding volume.
Depiction of a cylindrical magnet in gray, embedded in a volume of air in blue.
Creating an electromagnetic model always comprises the same steps:
The first step is to create the geometry.
When modeling a permanent magnet, it is important to consider the surrounding volume. This allows the field extending outward from the device into the surrounding volume to be simulated.
In principal, the surrounding volume should be unbounded. Since an unbounded domain cannot be simulated, exterior boundaries are introduced and are known as artificial boundaries. These artificial boundaries limit the extent of the model to a region of interest. A condition must be applied at these exterior boundaries to obtain a unique solution.
The surrounding volume needs to be sufficiently large compared to the object inside. The reason is to avoid that the boundary conditions applied at the artificial, exterior boundary affect the computations of the field in or on the device.
To decide how large the surrounding sphere must be, it is common practice to perform a convergence test with respect to the size of the surrounding domain. Such a convergence test is carried out in the Convergence of magnetostatic models section but omitted here.
This concludes the geometry setup. Next, the materials used are considered. To do that, the variables are set up. The dependent variable ![]() represents the scalar magnetic potential in the
represents the scalar magnetic potential in the ![]() ,
, ![]() and
and ![]() directions, respectively.
directions, respectively.
The model consists of an air domain and a magnet domain. In the air domain, the magnetization is 0 and in the magnet domain the magnetization is ![]() . The different values of the magnetization are expressed through a Piecewise function. A RegionMemberFunction provides the bounds where the magnet magnetization is present.
. The different values of the magnetization are expressed through a Piecewise function. A RegionMemberFunction provides the bounds where the magnet magnetization is present.
The use of Piecewise allows for an efficient evaluation of the PDE coefficients, and it is discussed in detail in the section Efficient Evaluation of PDE Coefficients of the Finite Element Method Usage Tips tutorial.
At the outer boundary of the surrounding sphere, a condition is set such that the magnetic potential is 0.
An easy way to generate a mesh that preserves the internal boundaries of the magnet is to create the RegionDifference of the sphere and magnet but then to request both regions be meshed with "RegionHoles" None.
This gives a short overview of the workflow. To keep things simple, the example made use of the function RegionMember. This, however, has as a consequence that when secondary fields are computed, possible discontinuities cannot be resolved properly. The next sections will discuss and address the limitation that comes up when computing discontinuous secondary fields that would be problematic in this case. Once this more elaborate process is established, it can also be applied to the cylindrical magnet example, which is then done in the multimaterial section.
Geometry
The next example shows how to perform a magnetostatic analysis of a horseshoe magnet and a coin in front of it. For this example, a predefined boundary element mesh is loaded.
The geometric model contains a 1/4 geometry of a horseshoe permanent magnet, a coin in front of it and a bounding box. The reduction to the 1/4 geometry is possible due to the symmetries that the geometry has. One plane of symmetry is the ![]() plane and the second plane of symmetry is the
plane and the second plane of symmetry is the ![]() plane.
plane.
For the actual computation, only the 1/4 geometry will be used, but it is possible to visualize the full geometry.
The geometry includes two iron regions: one in the horseshoe magnet and the other in the coin. The actual magnet region is located at the tip of the horseshoe magnet, and the surrounding domain consists of air.
One thing to keep in mind is the scale used in the geometric model. If the length of the boundary mesh is, for example, in units of meters, then the material parameters will need to be specified in consistent units. In this specific case, the units of the boundary mesh are in meters.
More information on generating or importing 3D geometric models can be found in the Using OpenCascadeLink tutorial.
Mesh Generation
To perform a finite element analysis, the boundary mesh representation of the geometric model needs to be discretized into a mesh. In this same process, different material regions are specified with element markers.
More information about the mesh generation process can be found in the ElementMesh generation tutorial. Another option is to import a mesh generated with third-party software. Some common mesh file formats can be imported with the help of the FEMAddOns.
Material Parameters
The next step is to assign material parameters. Generally, all parameters for electromagnetics models are collected in an Association pars that includes the necessary parameter values.
The geometry consists of several regions: two iron regions, a magnet and an air region. Distinct material models must be set up for each of these regions. The iron and air regions use a linear constitutive material model given by:
where ![]() is the unitless relative permeability and
is the unitless relative permeability and ![]() [
[![]() ] is the vacuum permeability.
] is the vacuum permeability.
A default value ![]() [
[![]() ] of the vacuum permeability is used throughout the whole monograph. However, the "VacuumPermeability" parameter can be specified if the constant should have a different value, like 1. This can be useful to scale the equation.
] of the vacuum permeability is used throughout the whole monograph. However, the "VacuumPermeability" parameter can be specified if the constant should have a different value, like 1. This can be useful to scale the equation.
For iron, a relative permeability of 5000 is applied, while for air, a value of 1 is used. The magnet, strictly speaking, does not have a permeability. Instead, it has a magnetization vector ![]() , shown later. In the magnet region, a relative permeability of
, shown later. In the magnet region, a relative permeability of ![]() is set up.
is set up.
To geometrically distinguish between the regions, ElementMarker will be used. This approach is particularly useful for handling more complex geometries. More information about the use of ElementMarker can be found in the ElementMesh generation tutorial.
Permanent magnets are made of hard ferromagnetic materials, which produce magnetic flux even in the absence of an externally applied field. In this model, a magnetization vector ![]() is used to describe the permanent magnet; other ways exist and will be discussed later in the Magnetic materials section.
is used to describe the permanent magnet; other ways exist and will be discussed later in the Magnetic materials section.
For the magnet region, the general form of the magnetostatic equation is used:
where ![]() is the magnetization vector in units of [
is the magnetization vector in units of [![]() ]. In the magnet region, the magnetization vector
]. In the magnet region, the magnetization vector ![]() is
is ![]() . In the iron and air region, there is no magnetization, and thus the magnetization vector
. In the iron and air region, there is no magnetization, and thus the magnetization vector ![]() there is
there is ![]() .
.
The MagnetostaticPDEComponent will generate a single equation that includes both constitutive relations into:
This equation is valid for modeling purposes, provided that the correct parameter values are appropriately assigned to each region. When the MagnetostaticPDEComponent is evaluated with the parameter setup created in this section, the equation ![]() is obtained in the magnet region, because here
is obtained in the magnet region, because here ![]() was set. When evaluated in the air/iron region, the equation
was set. When evaluated in the air/iron region, the equation ![]() is obtained, as in the air/iron region the magnetization vector components are set to 0.
is obtained, as in the air/iron region the magnetization vector components are set to 0.
Material parameters where the values are given as Quantity objects can be used. A complete list of property names to specify material properties needed can be found on the reference page of MagnetostaticPDEComponent. Specifying a magnetic material as "Material"->Entity is currently not possible.
Units
Should the units of the geometry be different from the material units, then the material units can be scaled.
Internally, all material data units are converted to "SIBase" units. As a consequence, the default unit of length is "Meters". If the units of the geometry are also in meters, then nothing needs to be changed. If the units of the geometry are not in meters, then either the PDE and material properties need to be scaled to the units of the geometry or the geometry needs to be scaled to "Meters". To scale the units of the PDE and material parameters, the parameter "ScaleUnits" can be given. If not explicitly stated otherwise, examples in this tutorial use the default "SIBase" units.
More information about the use of units in PDE models can be found in the PDEModels Best Practice tutorial.
Boundary Conditions
Boundary conditions must be defined to fully specify the problem. In essence, this is done by applying a DirichletCondition or NeumannValue at the boundaries, respectively. The various boundary conditions typically used to model magnetostatic devices will be discussed in detail in the section Boundary conditions. The main purpose of this section is to establish the positions where the boundary conditions are to be applied.
In this example, the magnetic field is symmetric with respect to the ![]() plane and antisymmetric with respect to the
plane and antisymmetric with respect to the ![]() plane. Antisymmetry means that the resulting field has the property
plane. Antisymmetry means that the resulting field has the property ![]() , and symmetry means that field has the propriety that
, and symmetry means that field has the propriety that ![]() . To ensure that the magnetic field has this behavior, boundary conditions that enforce these symmetries are applied at these planes.
. To ensure that the magnetic field has this behavior, boundary conditions that enforce these symmetries are applied at these planes.
At the antisymmetry plane, ![]() , the magnetic field is perpendicular to the boundary. To force the magnetic field to be perpendicular to the boundary, a zero magnetic scalar potential condition needs to be applied. This is essentially a DirichletCondition type condition that sets the scalar magnetic potential
, the magnetic field is perpendicular to the boundary. To force the magnetic field to be perpendicular to the boundary, a zero magnetic scalar potential condition needs to be applied. This is essentially a DirichletCondition type condition that sets the scalar magnetic potential ![]() at the boundary to a specific value. A way to find the positions where the boundary conditions are applied is to visualize them together with the outline of the geometry defined above.
at the boundary to a specific value. A way to find the positions where the boundary conditions are applied is to visualize them together with the outline of the geometry defined above.
The zero magnetic scalar potential condition will be applied at the antisymmetry plane ![]() .
.
At the symmetry plane, ![]() , the magnetic field is tangential to the boundary, which can be achieved by using a magnetic insulation boundary condition, equivalent to a zero Neumann value.
, the magnetic field is tangential to the boundary, which can be achieved by using a magnetic insulation boundary condition, equivalent to a zero Neumann value.
If no boundary condition is applied on any part of the boundary, then the default zero Neumann condition is used. This means that to obtain the effect of a magnetic insulation boundary condition, nothing needs to be done because it happens automatically.
The remaining surfaces represent exterior boundaries of the surrounding box. At these boundaries, zero NeumannValue values are also applied. These could also be omitted, as they are automatically satisfied.
For more complicated geometries, a different technique to specify where boundary condition apply may be more appropriate and is shown in the Markers section of the element mesh generation tutorial.
Magnetostatic Analysis
In a magnetostatic analysis, the primary objective is to determine the magnetic scalar potential distribution, ![]() , and, as secondary derived quantities, the magnetic flux density
, and, as secondary derived quantities, the magnetic flux density ![]() in units of [
in units of [![]() ] and the magnetic field intensity
] and the magnetic field intensity ![]() in units of [
in units of [![]() ].
].
Note how the equation ![]() is obtained when the equation is evaluated in the magnet region. When it is evaluated in the air/iron region, the equation
is obtained when the equation is evaluated in the magnet region. When it is evaluated in the air/iron region, the equation ![]() is obtained, as explained in detail in the Materials parameters section.
is obtained, as explained in detail in the Materials parameters section.
Next, a zero magnetic scalar potential ![]() will be applied at
will be applied at ![]() . At the exterior boundary, this will ensure that the magnetic field lines will be perpendicular to the boundary, an antisymmetric behavior. A MagneticPotentialCondition is equivalent to specifying a DirichletCondition.
. At the exterior boundary, this will ensure that the magnetic field lines will be perpendicular to the boundary, an antisymmetric behavior. A MagneticPotentialCondition is equivalent to specifying a DirichletCondition.
The remaining boundary conditions are NeumannValue zero boundary conditions and can be omitted.
The result is an InterpolatingFunction object, which gives the magnetic scalar potential distribution ![]() .
.
More information about the solution process and its options can be found in the NDSolve Options for Finite Elements tutorial.
Post-processing
The primary solution of the magnetostatic PDE model is the magnetic scalar potential ![]() .
.
The magnetic scalar potential ![]() lacks a physical meaning. What is, however, of interest is the magnetic field intensity
lacks a physical meaning. What is, however, of interest is the magnetic field intensity ![]() and the magnetic flux density
and the magnetic flux density ![]() , and these fields are recovered from the scalar potential
, and these fields are recovered from the scalar potential ![]() .
.
Both the magnetic field intensity ![]() and the magnetic flux density
and the magnetic flux density ![]() can be discontinuous at the material interface. More information about these conditions can be found in the section Conditions at material interfaces. To address these discontinuities, a DiscontinuousInterpolatingFunction or EvaluateOnElementMesh is used. This process will be shown next.
can be discontinuous at the material interface. More information about these conditions can be found in the section Conditions at material interfaces. To address these discontinuities, a DiscontinuousInterpolatingFunction or EvaluateOnElementMesh is used. This process will be shown next.
First, convert the magnetic scalar potential function ![]() to a DiscontinuousInterpolatingFunction.
to a DiscontinuousInterpolatingFunction.
The magnetic field intensity ![]() is the gradient of the magnetic scalar potential and will be computed in a second step.
is the gradient of the magnetic scalar potential and will be computed in a second step.
For a three-dimensional model, the ![]() -field computed with the function Grad returns a list of three DiscontinuousInterpolatingFunction with the three independent variables
-field computed with the function Grad returns a list of three DiscontinuousInterpolatingFunction with the three independent variables ![]() ,
, ![]() and
and ![]() each.
each.
Note that when the ![]() field is evaluated exactly at the discontinuity, the returned value will be the value of iron. In some cases, it may be preferable to obtain the value of air. The behavior of which subdomain takes precedence can be controlled. DiscontinuousInterpolatingFunction or EvaluateOnElementMesh functions will prioritize a value from one of the subdomains. More details about how to model multimaterial models can be found in the Multimaterial section.
field is evaluated exactly at the discontinuity, the returned value will be the value of iron. In some cases, it may be preferable to obtain the value of air. The behavior of which subdomain takes precedence can be controlled. DiscontinuousInterpolatingFunction or EvaluateOnElementMesh functions will prioritize a value from one of the subdomains. More details about how to model multimaterial models can be found in the Multimaterial section.
Various components of the magnetic field can be accessed by using Part.
The magnetization vector ![]() and the relative permeability
and the relative permeability ![]() are Piecewise functions in this case, resulting in a discontinuity at the material boundary. EvaluateOnElementMesh can be used to create a DiscontinuousInterpolatingFunction from them.
are Piecewise functions in this case, resulting in a discontinuity at the material boundary. EvaluateOnElementMesh can be used to create a DiscontinuousInterpolatingFunction from them.
To visualize the antisymmetric 1/4 of the field, the antisymmetric behavior of the field must be considered. At positive ![]() values, the field is
values, the field is ![]() and for
and for ![]() , the field is
, the field is ![]() .
.
A DensityPlot is used to visualize the magnetic flux density at the plane ![]() .
.
Note the discontinuity in the magnetic flux density between the interface of the entire magnet and the air region.
This same workflow can be applied to any type of geometry.
Remember that the magnetic scalar potential can only be used in models where no current is present. Otherwise, the magnetic vector potential, ![]() , must be used.
, must be used.
Equations
Overview
This section gives an introduction on creating magnetostatics partial differential equation models. Generally speaking, magnetostatics is the subfield of electromagnetics that deals with magnetic fields produced either by direct currents (DC) in a conductor or, alternatively, by permanent magnets.
In magnetostatics, two different formulations, derived from Maxwell's equations, are used for modeling magnetostatic fields. The first uses a scalar magnetic potential ![]() , and the second makes use of the vector magnetic potential
, and the second makes use of the vector magnetic potential ![]() . In this monograph, only the scalar magnetic potential
. In this monograph, only the scalar magnetic potential ![]() formulation is addressed. The scalar magnetic potential is mainly used to model permanent magnets.
formulation is addressed. The scalar magnetic potential is mainly used to model permanent magnets.
Starting with an explanation of Maxwell's equations used for magnetostatics, a derivation of the scalar magnetic potential equation, the ![]() formulation for short, is given. That is followed by an introduction of the constitutive relations that explain how the magnetic field interacts with matter.
formulation for short, is given. That is followed by an introduction of the constitutive relations that explain how the magnetic field interacts with matter.
The most general form of the equation of the scalar magnetic potential ![]() formulation is:
formulation is:
The dependent variable in this equation is the scalar magnetic potential ![]() in units of [
in units of [![]() ], which varies with position
], which varies with position ![]() . The equation is made up of a diffusive term
. The equation is made up of a diffusive term ![]() with the vacuum permeability
with the vacuum permeability ![]() [
[![]() ] as the diffusion coefficient. A second term is the derivative term
] as the diffusion coefficient. A second term is the derivative term ![]() , in which the variable
, in which the variable ![]() [
[![]() ] is the magnetization vector. The
] is the magnetization vector. The ![]() formulation is used in 2D, 2D axis symmetric and 3D geometries; 1D cases cannot be modeled with this equation.
formulation is used in 2D, 2D axis symmetric and 3D geometries; 1D cases cannot be modeled with this equation.
Note that this equation does not have a source term; in other words, it is set to 0, which means that the equation cannot be used if currents are present. Since the ![]() formulation is used only in static cases and when the model or device is free of currents, it usually used to model permanent magnets. In other cases, when sources are present, the vector magnetic potential
formulation is used only in static cases and when the model or device is free of currents, it usually used to model permanent magnets. In other cases, when sources are present, the vector magnetic potential ![]() formulation should be used.
formulation should be used.
From Maxwell's Equations to the Scalar Potential Magnetostatic Equation
The derivation of the magnetostatic equation starts from Maxwell's equations:
where ![]() is the gradient operator,
is the gradient operator, ![]() is the dot product and
is the dot product and ![]() is the cross product. All vector-valued quantities are bold.
is the cross product. All vector-valued quantities are bold.![]() [
[![]() ] and
] and ![]() [
[![]() ] are the electric and magnetic field intensities, respectively.
] are the electric and magnetic field intensities, respectively. ![]() [
[![]() ] is the electric flux density, and
] is the electric flux density, and ![]() [
[![]() ]
]![]() [
[![]() ] is the magnetic flux density, sometimes also called magnetic induction. Flux density refers to the flow though an area.
] is the magnetic flux density, sometimes also called magnetic induction. Flux density refers to the flow though an area. ![]() [
[![]() ] is the electric current flux density, commonly called electric current density, and
] is the electric current flux density, commonly called electric current density, and ![]() [
[![]() ] is electric charge density, and they represent sources of a magnetic and an electric field, respectively. SI units are used throughout the tutorial.
] is electric charge density, and they represent sources of a magnetic and an electric field, respectively. SI units are used throughout the tutorial.
In the static regime, time variations of quantities become zero (![]() ). So, Maxwell's equations can be written in the following form:
). So, Maxwell's equations can be written in the following form:
A direct consequence of neglecting the time-derivative terms is that the electric and magnetic fields are no longer coupled. The static regime also implies that any time-dependent effects such as inductive effects need not be considered.
As Maxwell's equations are no longer coupled, it is possible to solve solely for the electric or magnetic field. This means there are two sets of equations: one describing the electrostatic case and the other describing the magnetostatic case.
The magnetostatic case consists of the following equations:
These equations, and the corresponding constitutive relation for ![]() and
and ![]() , describe magnetostatic phenomena [Ida & Bastos, 2013].
, describe magnetostatic phenomena [Ida & Bastos, 2013].
Ampere's law ![]() helps to understand how a current density vector
helps to understand how a current density vector ![]() generates a rotating magnetic field. For example, if a current is flowing through a straight wire, this will generate circular loops of magnetic fields around the wire.
generates a rotating magnetic field. For example, if a current is flowing through a straight wire, this will generate circular loops of magnetic fields around the wire.
The second equation, the Gauss law of magnetism ![]() , says that the magnetic flux
, says that the magnetic flux ![]() is conservative and thus, a magnetic flux will not have a source or a sink. In other words, there are no isolated magnetic charges that produce magnetic fields.
is conservative and thus, a magnetic flux will not have a source or a sink. In other words, there are no isolated magnetic charges that produce magnetic fields.
Finally, it is important to note that although Faraday's law ![]() will not be used to derive the equation, it still provides valuable insights. Faraday's law indicates that in a magnetostatic situation, electric fields are not generated by time-varying magnetic fields. However, the fact that the curl is zero does not imply that the electric field
will not be used to derive the equation, it still provides valuable insights. Faraday's law indicates that in a magnetostatic situation, electric fields are not generated by time-varying magnetic fields. However, the fact that the curl is zero does not imply that the electric field ![]() is zero in a magnetostatic case [Ida & Bastos, 2013], as an external electric field can always exist but it will not affect a magnetostatic model.
is zero in a magnetostatic case [Ida & Bastos, 2013], as an external electric field can always exist but it will not affect a magnetostatic model.
These reduced versions of Maxwell's equations together with the corresponding constitutive equations will help to derive the potential and the equation needed to model static magnetic fields free of currents.
The ![]() magnetostatic equation is:
magnetostatic equation is:
The exact derivation of the equation in terms of ![]() will be shown in the subsequent sections.
will be shown in the subsequent sections.
Magnetic Materials
The next question to answer is how a material interacts with an external magnetic field. Also of interest is how it is possible that permanent magnets can generate and maintain their own magnetic fields without the need of an electric current.
The way to describe and understand how a material interacts magnetically is through the magnetization vector ![]() [
[![]() ]. The magnetization vector
]. The magnetization vector ![]() is a vector field that expresses the density of permanent or induced magnetic dipole moments in a material. Magnetic dipoles are the origin of the magnetic properties of a material. The magnetization vector describes how a material responds to an applied magnetic field as well as the way the material changes the field.
is a vector field that expresses the density of permanent or induced magnetic dipole moments in a material. Magnetic dipoles are the origin of the magnetic properties of a material. The magnetization vector describes how a material responds to an applied magnetic field as well as the way the material changes the field.
On a quantum level of a material, magnetic dipole moments originate from both the movement of electrons orbiting around nuclei in atoms and the spin of electrons. A net magnetization occurs when an external magnetic field is applied and the magnetic moments align with the field. Otherwise, the net magnetic moment will be zero, due to the random orientation of the magnetic dipoles.
Magnetic dipole moment in a volume represented by small magnets. On the left: No external magnetic field ![]() is applied. On the right: An external magnetic field is applied and the magnetic moments align with the field [Domke, 2011].
is applied. On the right: An external magnetic field is applied and the magnetic moments align with the field [Domke, 2011].
Faraday's law says that magnetic fields are generated by electric currents flowing through a conductor. Similarly, in magnetic materials, the magnetic fields arise from the collective behavior of magnetic dipole moments per unit volume. This collective behavior can be described as a bound current, which generates a magnetization vector, ![]() . Just as Faraday's law explains how electric currents create magnetic fields,
. Just as Faraday's law explains how electric currents create magnetic fields, ![]() , the bound current in magnetic materials produces the magnetization vector
, the bound current in magnetic materials produces the magnetization vector ![]() :
:
where ![]() is the bound volume current density. A bound current refers to a type of current that arises within materials, particularly in magnetized materials, due to the alignment of magnetic dipoles. It is important to distinguish a
is the bound volume current density. A bound current refers to a type of current that arises within materials, particularly in magnetized materials, due to the alignment of magnetic dipoles. It is important to distinguish a ![]() current from a free current. Bound currents are associated with molecular or atomic magnetic moments, including the spin of electrons. These type of currents are called "bound" because they are tied to the positions of the atoms or molecules within the material.
current from a free current. Bound currents are associated with molecular or atomic magnetic moments, including the spin of electrons. These type of currents are called "bound" because they are tied to the positions of the atoms or molecules within the material.
On the other hand, free currents are just conduction currents that follow Ohm's law.
In free space, ![]() , the following equation is used:
, the following equation is used:
On the contrary, in a material medium where ![]() ,
, ![]() will have a contribution from both the conduction current
will have a contribution from both the conduction current ![]() and the bound current
and the bound current ![]() :
:
Expressing ![]() in terms of
in terms of ![]() , through Eqn. 1. Then Eqn.2 becomes:
, through Eqn. 1. Then Eqn.2 becomes:
Comparing Eqn. 3 with Eqn. 4, the following definition for ![]() is deduced:
is deduced:
and by rearranging this equation, the constitutive relation of ![]() with
with ![]() is obtained:
is obtained:
This constitutive relation holds for all magnetic materials whether they are linear or not.
Alternatively, a magnetic polarization ![]() can be defined, such that
can be defined, such that ![]() . The relation between the magnetic polarization and the magnetization vector is then given by
. The relation between the magnetic polarization and the magnetization vector is then given by ![]() . This relation is also valid for both linear and nonlinear materials.
. This relation is also valid for both linear and nonlinear materials.
Now that the constitutive relations have been defined, the derivation of the magnetostatic equation can follow.
Scalar potential formulation
The equation used in the ![]() formulation is derived from Gauss's law for magnetics:
formulation is derived from Gauss's law for magnetics:
but expressed in terms of the magnetic scalar potential ![]() and including material properties.
and including material properties.
First, the constitutive relation of ![]() and
and ![]() is substituted into Eqn. 5:
is substituted into Eqn. 5:
When there are no free currents, which means that ![]() , and under static conditions, it is possible to define a magnetic scalar potential much like the scalar electric potential
, and under static conditions, it is possible to define a magnetic scalar potential much like the scalar electric potential ![]() . So, under the condition that
. So, under the condition that ![]() , Ampere's law becomes:
, Ampere's law becomes:
This setting ![]() is done because generally speaking, for fields the following equation can be deduced:
is done because generally speaking, for fields the following equation can be deduced:
which states that the curl of the gradient of any scalar function ![]() is zero. Thus, comparing Eqn. 6 with Faraday's law (
is zero. Thus, comparing Eqn. 6 with Faraday's law (![]() ), it is deduced that
), it is deduced that ![]() can be represented as the gradient of a function
can be represented as the gradient of a function ![]() :
:
The negative sign is added to correctly describe the direction of the magnetic field ![]() in relation to the magnetic scalar potential
in relation to the magnetic scalar potential ![]() . Just as
. Just as ![]() points in the direction of decreasing electric potential,
points in the direction of decreasing electric potential, ![]() points in the direction of decreasing magnetic scalar potential.
points in the direction of decreasing magnetic scalar potential.
Now that the magnetic scalar potential has been defined, the final version of the ![]() magnetostatic equation can be obtained by substituting it in Eqn. 7:
magnetostatic equation can be obtained by substituting it in Eqn. 7:
Linear magnetic materials
For linear materials, ![]() depends linearly on
depends linearly on ![]() such that:
such that:
where ![]() is a dimensionless quantity called magnetic susceptibility that measures how susceptible a material is to a magnetic field.
is a dimensionless quantity called magnetic susceptibility that measures how susceptible a material is to a magnetic field.
Substituting Eqn. 8 into ![]() yields the linear constitutive relation for magnetic materials:
yields the linear constitutive relation for magnetic materials:
where the unitless ![]() is the relative permeability given by:
is the relative permeability given by:
where ![]() is the absolute permeability in units of [
is the absolute permeability in units of [![]() ].
].
The relative permeability can depend on the space coordinates ![]() and vary in the region considered, i.e. an inhomogeneous material, or vary with direction, i.e. an anisotropic material.
and vary in the region considered, i.e. an inhomogeneous material, or vary with direction, i.e. an anisotropic material.
Next, the linear constitutive relation (Eqn. 9) is substituted into Gauss' law for magnetics:
Then, by substituting ![]() (Eqn. 10), the linear equation is obtained:
(Eqn. 10), the linear equation is obtained:
Both Eqns. 11 and 12 can be expressed through the MagnetostaticPDEComponent, as shown in the Model setup and Modeling magnetic materials sections.
Anisotropic materials
For anisotropic materials, like crystals, the relative permeability ![]() is a tensor. In the 3D case, the tensor has nine components:
is a tensor. In the 3D case, the tensor has nine components:
where ![]() is the relative permeability tensor.
is the relative permeability tensor. ![]() and
and ![]() are called the principal relative permeability coefficients and off-diagonal permeability coefficients, respectively.
are called the principal relative permeability coefficients and off-diagonal permeability coefficients, respectively.
Classification of Magnetic Materials
In general, the relative permeability ![]() or the magnetic susceptibility
or the magnetic susceptibility ![]() are used to classify materials depending on their response to external magnetic fields. There are basically two types of magnetic materials:
are used to classify materials depending on their response to external magnetic fields. There are basically two types of magnetic materials:
- Hard ferromagnetic materials, better known as permanent magnets. Permanent magnets are made from alloys, such as mixtures of neodymium, iron and boron (NdFeB) or from an alloy primarily composed of aluminum, nickel and cobalt (AlNiCo).
A material is said to be nonmagnetic if ![]() or
or ![]() , such as free space or air.
, such as free space or air.
Next, a detailed description of soft and hard magnetic materials is provided to better understand their differences, including how their values of ![]() vary in each case.
vary in each case.
First, soft diamagnetic and paramagnetic materials will be described, then ferromagnetic materials, which include soft and hard ferromagnetic materials.
Diamagnetic materials have a relative permeability slightly lower than one, ![]() , or a magnetic susceptibility lower than zero,
, or a magnetic susceptibility lower than zero, ![]() . The phenomenon of diamagnetism arises from the orbital angular momentum of electrons [Purcell, 2013]. These types of materials are slightly repelled by magnets, and this is because the diamagnetic moment points antiparallel to the external magnetic field. That is to say,
. The phenomenon of diamagnetism arises from the orbital angular momentum of electrons [Purcell, 2013]. These types of materials are slightly repelled by magnets, and this is because the diamagnetic moment points antiparallel to the external magnetic field. That is to say, ![]() is negative.
is negative.
Diamagnetism is a property of every atom and molecule, but often is outweighed by a different and stronger effect. A common diamagnetic material is copper, which has a relative permeability of 0.999991. Other diamagnetic materials possess a ![]() of the same order of magnitude. So, for most practical cases, it is assumed that
of the same order of magnitude. So, for most practical cases, it is assumed that ![]() for diamagnetic materials.
for diamagnetic materials.
Paramagnetic materials have a relative permeability slightly larger than one, ![]() , or a magnetic susceptibility higher than zero,
, or a magnetic susceptibility higher than zero, ![]() . The phenomenon of paramagnetism arises from the spin angular momentum of electrons [Purcell, 2013]. These types of materials are slightly attracted by magnets, and this is because the diamagnetic moment points parallel to the external magnetic field. That is to say,
. The phenomenon of paramagnetism arises from the spin angular momentum of electrons [Purcell, 2013]. These types of materials are slightly attracted by magnets, and this is because the diamagnetic moment points parallel to the external magnetic field. That is to say, ![]() is positive.
is positive.
The effect due to paramagnetism is negligible. A common diamagnetic material is aluminum, which has a relative permeability 0f 1.00000036. Therefore, as with diamagnetic materials, it is assumed that ![]() for paramagnetic materials.
for paramagnetic materials.
The most commonly known ferromagnetic material is iron. Ferromagnetic materials are of great importance in electromagnetic devices. This is mainly because ferromagnetic material have a relative permeability much larger than one, ![]() , or a magnetic susceptibility much higher than zero,
, or a magnetic susceptibility much higher than zero, ![]() . Iron, for example, can have a relative permeability in the order of
. Iron, for example, can have a relative permeability in the order of ![]() .
.
A ferromagnetic material like iron is composed of different domains where the spins are aligned, forming little pockets of magnetic domains all over the material. These magnetic pockets, when aligned, are what give ferromagnetic materials their strong magnetic properties. In essence, ferromagnetism arises from the spin angular momentum of electrons, but in a stronger manner than in paramagnetic materials. A deeper insight can be gained from a quantum mechanics perspective, which is omitted here. The interested reader is referred to [Purcell, 2013].
Apart from having a great relative permeability and being strongly attracted by magnets, ferromagnetic materials are also capable of conserving a magnetic moment in the absence of an external magnetic field. They retain their magnetization ![]() even after the external field has been removed.
even after the external field has been removed.
Another characteristic of ferromagnetic materials is that the relative permeability depends on the magnitude of the magnetic field, so even though ![]() holds, the linear constitutive relation,
holds, the linear constitutive relation, ![]() , no longer holds for ferromagnetic materials because of their nonlinear behavior. In addition to that,
, no longer holds for ferromagnetic materials because of their nonlinear behavior. In addition to that, ![]() is dependent on
is dependent on ![]() .
.
For details on how to model these nonlinearities, see the Modeling magnetic materials section.
Ferromagnetic materials show a second nonlinear behavior, which is in the relationship between ![]() and
and ![]() : The process of magnetization and demagnetization of ferromagnetic materials depends on the history of previous magnetizations. So in order to know how the material will behave, one needs to know in which state it was previously. As a consequence, the process of magnetization and demagnetization is not reversible along the same path. This nonlinear behavior is called hysteresis.
: The process of magnetization and demagnetization of ferromagnetic materials depends on the history of previous magnetizations. So in order to know how the material will behave, one needs to know in which state it was previously. As a consequence, the process of magnetization and demagnetization is not reversible along the same path. This nonlinear behavior is called hysteresis.
Due to hysteresis, the path followed when increasing the magnetic field is different from the path followed when decreasing it. This irreversibility indicates energy loss in the form of heat within each cycle of magnetization and demagnetization.
For ferromagnetic material, the only way to represent the relationship between ![]() and
and ![]() is through a magnetization curve called a
is through a magnetization curve called a ![]() -
-![]() curve.
curve.
Next, a closer examination of a ![]() -
-![]() curve and an explanation of the hysteresis effect will follow. A typical
curve and an explanation of the hysteresis effect will follow. A typical ![]() -
-![]() curve is shown below, accompanied by a material block where the blue arrows represent the magnetic domains of the material [Blinder, 2011].
curve is shown below, accompanied by a material block where the blue arrows represent the magnetic domains of the material [Blinder, 2011].
Interactive graph of a ![]() -
-![]() curve and below, a ferromagnetic visualization that shows how the magnetic domains behave according to the blue dot located on the
curve and below, a ferromagnetic visualization that shows how the magnetic domains behave according to the blue dot located on the ![]() -
-![]() curve. The purple, yellow and red dots show the location of the saturation field
curve. The purple, yellow and red dots show the location of the saturation field ![]() , the coercivity field
, the coercivity field ![]() and the remanence field
and the remanence field ![]() , respectively.
, respectively.
The interactive visualization shows a complete magnetization and demagnetization cycle of a ferromagnetic material.
When describing a ![]() -
-![]() curve, the focus is on the relationship between the magnitudes of these quantities, and therefore the bold vector notation is not used here, as the quantities in the
curve, the focus is on the relationship between the magnitudes of these quantities, and therefore the bold vector notation is not used here, as the quantities in the ![]() -
-![]() curve are referred to as scalar rather than vector quantities.
curve are referred to as scalar rather than vector quantities.
The description of the process of magnetization begins from the origin, that is to say, the material starts in a completely demagnetized state. There is no external magnetic field ![]() and the magnetic flux density is also zero
and the magnetic flux density is also zero ![]() . In this demagnetized state, the magnetic domains are oriented randomly. To align the domains, an external magnetic field
. In this demagnetized state, the magnetic domains are oriented randomly. To align the domains, an external magnetic field ![]() intensity must be applied to the material by increasing
intensity must be applied to the material by increasing ![]() . The domains will begin to align themselves in the direction of the magnetic field
. The domains will begin to align themselves in the direction of the magnetic field ![]() and the material will become magnetized, acquiring a magnetization
and the material will become magnetized, acquiring a magnetization ![]() , and start to produce a magnetic flux density
, and start to produce a magnetic flux density ![]() .
.
As ![]() is increased further, a point is reached where the material becomes saturated. Now all domains are aligned in the same direction. At this point, shown in purple, the saturation value,
is increased further, a point is reached where the material becomes saturated. Now all domains are aligned in the same direction. At this point, shown in purple, the saturation value, ![]() of the magnetic flux is reached. The material is now fully magnetized and the magnetization
of the magnetic flux is reached. The material is now fully magnetized and the magnetization ![]() remains constant beyond that.
remains constant beyond that.
To demagnetize the material, a magnetic field ![]() in the opposite direction must be applied. When
in the opposite direction must be applied. When ![]() is reduced to zero, the flux density is not reduced to zero because some of the magnetic domains will resist changing the applied
is reduced to zero, the flux density is not reduced to zero because some of the magnetic domains will resist changing the applied ![]() field. At
field. At ![]() ,
, ![]() reaches a value of
reaches a value of ![]() , known as the remanent magnetic flux density, shown in red. The fact that the material remains magnetized without an external field is the characteristic behavior of ferromagnetic materials. The effect is due to the resistance of the magnetic domains to align to the magnetic field
, known as the remanent magnetic flux density, shown in red. The fact that the material remains magnetized without an external field is the characteristic behavior of ferromagnetic materials. The effect is due to the resistance of the magnetic domains to align to the magnetic field ![]() applied in the opposite direction.
applied in the opposite direction.
If the blue dot is placed at ![]() , it can be seen that the domains will not be perfectly aligned. As a consequence, the magnetic flux density
, it can be seen that the domains will not be perfectly aligned. As a consequence, the magnetic flux density ![]() will lag behind the changes in
will lag behind the changes in ![]() . This lagging is what is known as hysteresis.
. This lagging is what is known as hysteresis.
If ![]() is increased further in the opposite direction, eventually a point is reached where the material becomes completely demagnetized, with
is increased further in the opposite direction, eventually a point is reached where the material becomes completely demagnetized, with ![]() . The value of
. The value of ![]() to achieve this is named the coercive field intensity
to achieve this is named the coercive field intensity ![]() , shown in yellow.
, shown in yellow.
By further increasing the value of ![]() in the negative direction, another saturation point is reached. Continuing to increase in the reverse direction returns to the previous saturation point, forming a closed curve called a hysteresis loop.
in the negative direction, another saturation point is reached. Continuing to increase in the reverse direction returns to the previous saturation point, forming a closed curve called a hysteresis loop.
The ![]() -
-![]() curve, and in consequence the area enclosed by the curve, varies from one material to another. This area enclosed by the curve gives the energy loss per unit volume during one cycle.
curve, and in consequence the area enclosed by the curve, varies from one material to another. This area enclosed by the curve gives the energy loss per unit volume during one cycle.
At any point on the curve , ![]() is given by the ratio
is given by the ratio ![]() /
/![]() , and by knowing
, and by knowing ![]() and
and ![]() , one easily can get a value for
, one easily can get a value for ![]() .
.
Ferromagnetic materials are also temperature dependent, so when heated above a specific value, they lose their magnetic properties. This critical temperature value is known as the Curie temperature.
It is important to note that the curve starting from the origin, known as the initial magnetization curve, will never be reproduced again unless the material is heated above its Curie temperature.
Last, the ![]() -
-![]() curve of a material allows one to identify if the material is a soft or hard ferromagnetic. This is shown in the following subsections.
curve of a material allows one to identify if the material is a soft or hard ferromagnetic. This is shown in the following subsections.
Soft ferromagnetic materials are materials that when an external magnetic field is no longer applied to them, do not retain a significant remanent flux density ![]() . They are characterized by having a low retentivity and they are typically used in electromagnets.
. They are characterized by having a low retentivity and they are typically used in electromagnets.
A soft ferromagnetic material will have a relatively small area under the ![]() -
-![]() due to their low
due to their low ![]() and
and ![]() values. The most common example of a soft ferromagnetic material is iron.
values. The most common example of a soft ferromagnetic material is iron.
Hard magnetic materials are materials that have a high retentivity, meaning that they retain a significant remanent magnetic flux ![]() . These hard magnetic materials are called permanent magnets. Permanent magnets also have a high coercivity, meaning they have high
. These hard magnetic materials are called permanent magnets. Permanent magnets also have a high coercivity, meaning they have high ![]() values and are hard to demagnetize. This values correlate to the much larger area under their
values and are hard to demagnetize. This values correlate to the much larger area under their ![]() -
-![]() curve.
curve.
Coercivity is defined as the intensity of the applied magnetic field required to reduce the magnetization of a material to zero after the material has been magnetized to saturation.
The section on modeling magnetic materials will examine the different approaches to modeling ferromagnetic materials. The most common example of a hard ferromagnetic material is the alloy of neodymium, iron and boron (NdFeB).
Model Setup
The ![]() formulation equations used in this monograph can be generated by MagnetostaticPDEComponent. The most general magnetic scalar potential equation is given by:
formulation equations used in this monograph can be generated by MagnetostaticPDEComponent. The most general magnetic scalar potential equation is given by:
The ![]() formulation works for stationary analysis and can be solved for 2D, 2D axisymmetric and 3D models but not for 1D.
formulation works for stationary analysis and can be solved for 2D, 2D axisymmetric and 3D models but not for 1D.
To specify a PDE model, model variables vars and parameters pars need to be set up. Stationary variables are specified as ![]() , where the dependent variable
, where the dependent variable ![]() is the magnetic scalar potential in units of [
is the magnetic scalar potential in units of [![]() ] and the {x,y,…} are the independent spatial variables in units of [
] and the {x,y,…} are the independent spatial variables in units of [![]() ].
].
The following is a list of possible parameters pars that can be specified for a ![]() steady magnetostatic model free of currents:
steady magnetostatic model free of currents:
Note that this model definition uses inactive PDE operators. "Numerical Solution of Partial Differential Equations" has several sections that explain the use of inactive operators.
In a magnetostatic analysis of permanent magnets, time and frequency studies are not relevant or useful.
The use of "Magnetization", "RelativePermeability" and "RemanentMagneticFluxDensity" is shown in the Modeling magnetic materials section.
2D models
When the magnetic scalar potential ![]() varies in, say, the
varies in, say, the ![]() and
and ![]() directions and is constant in the third direction, say the
directions and is constant in the third direction, say the ![]() direction, a 3D model can be modeled as a 2D model in the
direction, a 3D model can be modeled as a 2D model in the ![]() -
-![]() plane.
plane.
A 2D model has the advantage that the computational cost in both CPU time and machine memory is much less than in the case of solving a full 3D model.
These types of symmetries are seen frequently in rotating electric machines, in which the field distribution is repeated in planes parallel to the cross section of the electric machine [Cardoso, 2018].
The image shows a rectangular magnet. The magnetic scalar potential ![]() is visualized in slices. It can be seen from the slices that the magnetic scalar potential does not vary with respect to the
is visualized in slices. It can be seen from the slices that the magnetic scalar potential does not vary with respect to the ![]() direction within the magnet. It is thus possible to model the domain in the
direction within the magnet. It is thus possible to model the domain in the ![]() -
-![]() plane only by making the implicit assumption that the bar magnet is infinitely long along the
plane only by making the implicit assumption that the bar magnet is infinitely long along the ![]() axis.
axis.
With this symmetry, the following equation is solved:
where ![]() [
[![]() ] is a thickness variable denoting thickness of the device in the
] is a thickness variable denoting thickness of the device in the ![]() direction.
direction.
The default value for the thickness is ![]() .
.
To show a 2D example, a permanent magnet is modeled through its rectangular cross section. Basically, the 3D cuboid is cut at, for example, ![]() . The magnet is also magnetized transversely in the direction of the
. The magnet is also magnetized transversely in the direction of the ![]() axis. A zero magnetic scalar potential is used at the exterior boundaries of the surrounding volume to enclose the field.
axis. A zero magnetic scalar potential is used at the exterior boundaries of the surrounding volume to enclose the field.
Since in the default case the element size is roughly the same as the magnet, the magnet region shown in red was refined to get a better accuracy in the solution.
The magnet will have a magnetization in the ![]() direction with a value of 4000. The air region will have a magnetization of zero.
direction with a value of 4000. The air region will have a magnetization of zero.
2D axisymmetric
An axisymmetric simulation can be performed when a 3D solid has an axis of revolution. An axisymmetric model uses a truncated cylindrical coordinate system in 2D with independent variables ![]() instead of the cylindrical coordinates
instead of the cylindrical coordinates ![]() . The cylindrical coordinate variable
. The cylindrical coordinate variable ![]() disappears because the system is rotationally symmetric about the
disappears because the system is rotationally symmetric about the ![]() axis.
axis.
The 2D magnetostatic axisymmetric equation for ![]() for linear materials is given as:
for linear materials is given as:
An axisymmetric model has the advantage that the computational cost in both CPU time and machine memory is much less than in the case of solving a full 3D model.
The MagnetostaticPDEComponent function can produce the axisymmetric form of the ![]() magnetostatic equation. To do so, the parameter "RegionSymmetry" is set to "Axisymmetric".
magnetostatic equation. To do so, the parameter "RegionSymmetry" is set to "Axisymmetric".
A 2D axisymmetric model can also be generated when using other constitutive relations.
In the next example, the cylinder magnet of the overview example will be modeled with a 2D axisymmetric approximation. The geometry will consist of a rectangle and a semicircle.
Inactive is used to preserve the internal boundaries.
Element markers will be used here to attribute different material properties to the subdomains.
The mesh is refined in the magnet region, because in the default case, the size of the surrounding elements is roughly the same size as the magnet, and that is too little to accurately resolve that part of the geometry. Also, the mesh is created with an accuracy goal slightly higher than the default to get an accurate solution of the boundary.
Modeling Magnetic Materials
There are many different ways to represent the behavior of a magnetic material. The choice of which model or constitutive relation to use depends on how much of the material's characteristics is intended to be incorporated.
There are basically two types of magnetic materials that can be modeled:
- Hard ferromagnetic materials, better known as permanent magnets. Permanent magnets are made from alloys, such as mixtures of neodymium, iron and boron (NdFeB), or from an alloy primarily composed of aluminum, nickel and cobalt (AlNiCo)
The next sections explain in detail how to model soft and hard magnetic materials using MagnetostaticPDEComponent and its different parameters inputs.
The use of a full ![]() -
-![]() curve with hysteresis is not really needed in many cases. The following sections show how to model magnetic material if hysteresis is not to be considered. This will be appropriate in many, if not most cases. This will significantly simplify the models.
curve with hysteresis is not really needed in many cases. The following sections show how to model magnetic material if hysteresis is not to be considered. This will be appropriate in many, if not most cases. This will significantly simplify the models.
Soft magnetic materials
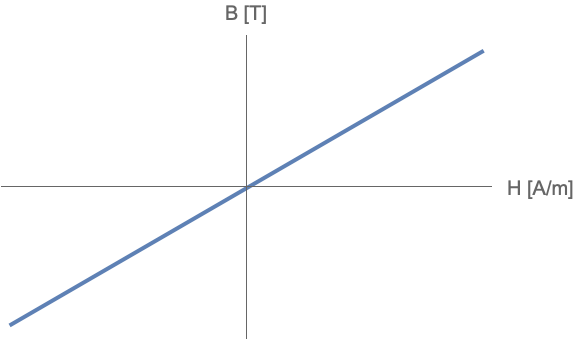
For soft magnetic materials like diamagnetic or paramagnetic materials, one can often simply use a relative permeability ![]() to describe the material.
to describe the material.
A linear relationship between ![]() and
and ![]() , given by
, given by ![]() .
.
For soft ferromagnetic materials, one can often simply use a relative permeability ![]() to describe the material or use a nonlinear
to describe the material or use a nonlinear ![]() , which can often be obtained from a simplified
, which can often be obtained from a simplified ![]() -
-![]() curve.
curve.
The constant relative permeability is used in soft iron if the fields are small, and a nonlinear ![]() is typically used to include the effect of magnetic saturation in soft ferromagnetic materials.
is typically used to include the effect of magnetic saturation in soft ferromagnetic materials.
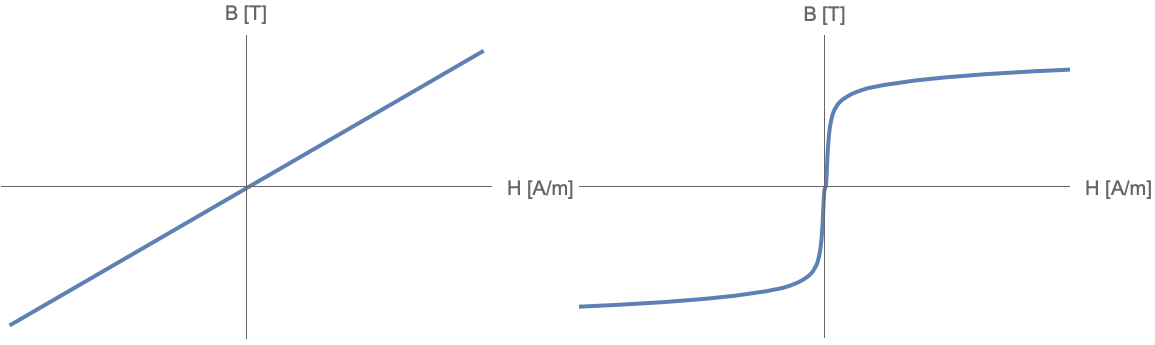
The figures below illustrate the types of simplified ![]() -
-![]() curves that are used to model soft ferromagnetic materials. Since a soft ferromagnetic material does not exhibit a big hysteresis, the
curves that are used to model soft ferromagnetic materials. Since a soft ferromagnetic material does not exhibit a big hysteresis, the ![]() -
-![]() curves used can be simpler than the ones presented in the Ferromagnetic materials section.
curves used can be simpler than the ones presented in the Ferromagnetic materials section.
On the left: a linear relationship between ![]() and
and ![]() , given by
, given by ![]() . On the right: a nonlinear relationship between
. On the right: a nonlinear relationship between ![]() and
and ![]() , given by
, given by ![]() .
.
In the Solving Partial Differential Equations with Finite Elements monograph, a motor model is shown that uses a nonlinear relative permeability ![]() obtained from a
obtained from a ![]() -
-![]() .
.
Hard ferromagnetic materials: Permanent magnets
In the following section, constitutive relations for permanent magnets are described, including:
The following sections show how to model hard ferromagnetic material if hysteresis is not to be considered. This will be appropriate in many, if not most cases.
The rare case where a full ![]() -
-![]() curve with hysteresis needs to be considered can be handled through the Jiles–Artherton model but is not considered here. Details on this model can be found in [Kumar & Tummuru, 2016].
curve with hysteresis needs to be considered can be handled through the Jiles–Artherton model but is not considered here. Details on this model can be found in [Kumar & Tummuru, 2016].
A conceptually simple approach to modeling permanent magnets is to describe the magnet though a magnetization vector ![]() according to the following equation:
according to the following equation:
This constitutive relation is used to describe rare earth permanent magnets that are already magnetized and that remain in this state. The overview example made use of this model for a cylindrical magnet.
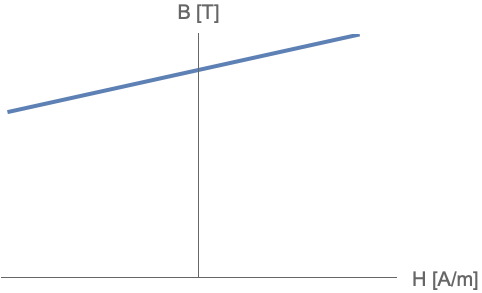
In the figure below, the ![]() -
-![]() behavior is illustrated by
behavior is illustrated by ![]() , where
, where ![]() is the offset of the line and the slope is
is the offset of the line and the slope is ![]() .
.
Simple ![]() -
-![]() behavior given by
behavior given by ![]() used for hard ferromagnetic materials.
used for hard ferromagnetic materials.
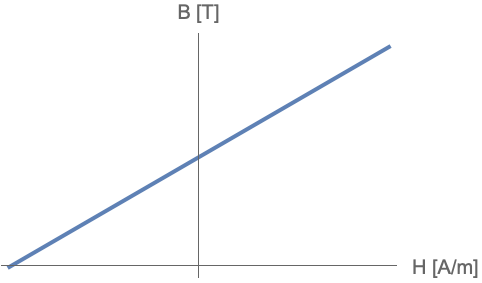
An alternative constitutive relation used to model permanent magnets is the remanent magnetic flux density. In general, manufacturers of permanent magnets provide magnetic characteristics in the form of a demagnetization curve, which is the second quadrant of the ![]() -
-![]() plane. These curves indicate the remanent flux density
plane. These curves indicate the remanent flux density ![]() , the coercive field intensity
, the coercive field intensity ![]() , and generally describe the way in which
, and generally describe the way in which ![]() and
and ![]() vary in the second quadrant. Permanent magnets, such as neodymium-iron-boron (NdFeB), exhibit an almost linear demagnetization curve like the one shown in the following graphic:
vary in the second quadrant. Permanent magnets, such as neodymium-iron-boron (NdFeB), exhibit an almost linear demagnetization curve like the one shown in the following graphic:
Simple ![]() -
-![]() behavior given by
behavior given by ![]() used for hard ferromagnetic materials.
used for hard ferromagnetic materials.
This constitutive law follows:
where ![]() is the remanent flux density in units of [
is the remanent flux density in units of [![]() ] and
] and ![]() is the unitless recoil permeability. Compared to the magnetization approach, this relation improves the modeled quality by the effect of demagnetizing caused by an externally applied field in the opposite direction to
is the unitless recoil permeability. Compared to the magnetization approach, this relation improves the modeled quality by the effect of demagnetizing caused by an externally applied field in the opposite direction to ![]() .
.
The recoil permeability ![]() is given by the ratio
is given by the ratio ![]() /
/![]() . The value of
. The value of ![]() given by manufacturers is actually the remanent flux density norm. To get the
given by manufacturers is actually the remanent flux density norm. To get the ![]() vector, the given value of
vector, the given value of ![]() is multiplied with a normalized direction field
is multiplied with a normalized direction field ![]() .
.
Using Eqn. 13 turns the magnetic scalar potential equation into:
In the next example, the same cylindrical magnet of the overview example is modeled, but here the magnet material will be expressed differently. In this case, the remanent magnetic flux density with a recoil permeability will be used. The magnet is made of the alloy neodymium-iron-boron (NdFeB).
For NdFeB materials, the remanent magnetic flux has a magnitude of ![]() [
[![]() ] and a recoil permeability of 1.05.
] and a recoil permeability of 1.05.
The values of the magnetic scalar potential are very similar to the ones from the overview example. The overview example has minimum and maximum values of ![]() and
and ![]() .
.
Modeling Anisotropic Materials
For anisotropic material, like crystals, the relative permeability ![]() is a 2-tensor. In the 3D case, the tensor has nine components:
is a 2-tensor. In the 3D case, the tensor has nine components:
where ![]() is the relative permeability tensor.
is the relative permeability tensor. ![]() and
and ![]() are called the principal relative permeability coefficients and off-diagonal permeability coefficients, respectively.
are called the principal relative permeability coefficients and off-diagonal permeability coefficients, respectively.
Anisotropic materials are found in advanced composite materials, magnetic recording media and certain types of sensors. These materials are used in fields like geophysics, material science and electrical engineering [Gutfleisch et al., 2011].
Multiple Materials
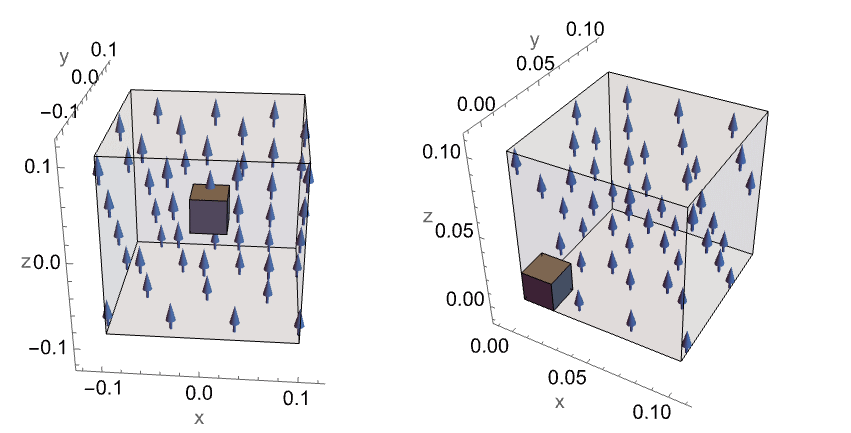
In magnetostatic models, the simulation domain always consists of multiple materials, primarily because it is necessary to account for the surrounding volume of a magnetic device. The overview example showed a first approach for simulating multimaterial regions, in which a cylindrical permanent magnet and its surrounding were modeled.
Depiction of a 3D cylinder magnet in gray and a sphere region of air surrounding the magnet, in blue.
In this section, the same model will be simulated, focusing on more specific details about the material interfaces.
First, the geometry is constructed.
In the overview example, to keep things simple, the example made use of the function RegionMember. This, however, had as a consequence that when secondary fields are computed, possible discontinuities cannot be resolved properly. A better way to do it is to use region markers for the specification of the different materials of the model and then use the function DiscontinuousInterpolatingFunction, as is done here.
Then, variables and parameters of the model are specified.
The use of Piecewise allows an efficient evaluation of the PDE coefficients, and it is discussed in detail in the section Efficient Evaluation of PDE Coefficients of the Finite Element Method Usage Tips tutorial.
Finally, the boundary conditions are defined and the PDE model is solved.
Now, you can proceed to study the material interfaces and their impact on the fields. When computing the magnetic flux density ![]() or the magnetic field intensity
or the magnetic field intensity ![]() , it is crucial to consider that at interfaces between materials, the fields can exhibit discontinuities. More information about these conditions can be found in the section on Conditions at material interfaces. Exploring how to handle these discontinuous interfaces is essential.
, it is crucial to consider that at interfaces between materials, the fields can exhibit discontinuities. More information about these conditions can be found in the section on Conditions at material interfaces. Exploring how to handle these discontinuous interfaces is essential.
In this example, ![]() will exhibit a discontinuity at the interface where
will exhibit a discontinuity at the interface where ![]() .
.
The previous plot shows the discontinuity across the material interface at ![]() . The values observed are
. The values observed are ![]() from the left and
from the left and ![]() from the right simultaneously.
from the right simultaneously.
Note that when using InterpolatingFunction, there is no control over what the value of the field at the interface is, which can be seen by the jiggled plot line. When evaluating an InterpolatingFunction at the material interface, it is somewhat random if the value of the one material subregion or the other subregion is given.
To address this issue, a DiscontinuousInterpolatingFunction is employed. This process will be shown next.
First, the electric potential function ![]() is converted to a DiscontinuousInterpolatingFunction.
is converted to a DiscontinuousInterpolatingFunction.
The magnetic field intensity ![]() will then be computed in a second step.
will then be computed in a second step.
The plot no longer shows random values from one of the material subregions. The plot shows only values that belong to the magnet subregion.
The remaining discontinuities observed in the plot are of a different nature. These arise when taking the derivative of the primary unknown variable, ![]() in this case. Such secondary values can exhibit discontinuities at the element boundaries. While these discontinuities are unavoidable, they can be reduced by refining the mesh. For more details, refer to the Discontinuity of Secondary Unknown Quantities section in the PDE Models Best Practices tutorial.
in this case. Such secondary values can exhibit discontinuities at the element boundaries. While these discontinuities are unavoidable, they can be reduced by refining the mesh. For more details, refer to the Discontinuity of Secondary Unknown Quantities section in the PDE Models Best Practices tutorial.
Note that the value that is returned at the discontinuity is the value of the magnet. The behavior of what takes precedence over what can be controlled. The DiscontinuousInterpolatingFunction function will prioritize a value from one of the subregions. The default is based on the order of material markers.
In this case, the default prioritization favors the magnet region, because the default chooses whatever region is first in the "MeshElementMarkerUnion" list. To demonstrate the usage of marker prioritization, gradients will be recalculated with a priority that favors the air region over the magnet region.
With this technique, precise control is exerted over which material subregion takes precedence. The fact that DiscontinuousInterpolatingFunction prioritizes the subregions based on markers also explains why an element mesh with markers is needed. In the overview example, no marker mesh was created for simplicity, and without the use of DiscontinuousInterpolatingFunction, the computation of the secondary quantities would not be accurate at the material interfaces. DiscontinuousInterpolatingFunction is very useful to compute values at the interface between two distinct materials, which can then be used in plots or as arguments for further computations.
Secondary Quantities
Once the simulation is completed, the solution for the dependent variables is obtained. Often, there is interest in quantities derived from the primary dependent variable. These derived quantities are called secondary quantities. Secondary quantities provide a deeper understanding of the model and include quantities like fields, forces, energy and energy-related parameters.
Fields
In magnetostatics, there are two different fields that can be computed from the magnetic scalar potential ![]() , the magnetic field intensity
, the magnetic field intensity ![]() and the magnetic flux density
and the magnetic flux density ![]() .
.
The magnetic field intensity is computed with the following equation:
The equation to use for computing the magnetic flux density ![]() will depend on the constitutive relations used. In the case of a linear material,
will depend on the constitutive relations used. In the case of a linear material, ![]() is computed with the following equation:
is computed with the following equation:
The accurate computation of magnetic fields ![]() and
and ![]() in permanent magnets is essential for the design, analysis and optimization of a wide range of electromagnetic devices and systems.
in permanent magnets is essential for the design, analysis and optimization of a wide range of electromagnetic devices and systems.
Energy
The magnetostatic energy ![]() is the energy that is stored in a magnetic field. For linear materials, the magnetostatic energy can be expressed by the following equation:
is the energy that is stored in a magnetic field. For linear materials, the magnetostatic energy can be expressed by the following equation:
where the magnetostatic energy density ![]() is:
is:
An example that computes the magnetostatic energy can be found in the Convergence of magnetostatic models section.
For nonlinear materials that have hysteresis effects, the previous equation no longer applies, and a more complicated expression is needed to account for the hysteresis effect.
For nonlinear materials, the energy density is obtained by integrating the ![]() relationship:
relationship:
where ![]() is the integration variable. The integration limit is from 0 to
is the integration variable. The integration limit is from 0 to ![]() , indicating a start from an unmagnetized state up to the current state
, indicating a start from an unmagnetized state up to the current state ![]() . Integration over the entire volume yields the total energy:
. Integration over the entire volume yields the total energy:
Magnetostatic Forces
This section shows how to compute magnetostatic forces between objects. This is useful, as many devices rely on magnetostatic forces for control and actuation. The Maxwell stress tensor ![]() will be used for the computation of magnetostatic forces and is introduced next.
will be used for the computation of magnetostatic forces and is introduced next.
Maxwell stress tensor
The Maxwell stress tensor ![]() is used to calculate electric and magnetic forces on objects. With the Maxwell stress tensor, the force can generally be expressed as:
is used to calculate electric and magnetic forces on objects. With the Maxwell stress tensor, the force can generally be expressed as:
where ![]() is the Maxwell stress tensor,
is the Maxwell stress tensor, ![]() is the unit normal vector,
is the unit normal vector, ![]() is the differential surface,
is the differential surface, ![]() is the domain surface boundary,
is the domain surface boundary, ![]() is the domain volume,
is the domain volume, ![]() is the differential volume, and
is the differential volume, and ![]() is the Poynting vector. In the magnetostatic case, there are no time dependencies, and the equation simplifies to:
is the Poynting vector. In the magnetostatic case, there are no time dependencies, and the equation simplifies to:
The componentwise definition of the full Maxwell stress tensor is:
where ![]() is the magnitude of E and
is the magnitude of E and ![]() is the Kronecker delta, which is 1 if the indices are the same and zero otherwise. In magnetostatics, the componentwise Maxwell stress tensor simplifies to:
is the Kronecker delta, which is 1 if the indices are the same and zero otherwise. In magnetostatics, the componentwise Maxwell stress tensor simplifies to:
The first index ![]() indicates the direction of the force, and the second index
indicates the direction of the force, and the second index ![]() indicates the direction of the surface.
indicates the direction of the surface.
In a 3D case, with spatial variables ![]() , the Maxwell stress tensor has nine components, as follows:
, the Maxwell stress tensor has nine components, as follows:
The Maxwell stress tensor ![]() is a force per unit area acting on a surface. To compute the actual stress
is a force per unit area acting on a surface. To compute the actual stress ![]() for a given surface, one takes the dot product with the desired surface normal such that:
for a given surface, one takes the dot product with the desired surface normal such that:
Then, ![]() is integrated over the surface of the object that the force acts on:
is integrated over the surface of the object that the force acts on:
For the complete derivation of the equation, refer to [Griffiths, 2017].
An equivalent formula that is easier to compute is [Ida & Bastos, 2013]:
Eqn. 14 is an alternative to compute ![]() and is used here. An electrostatic example is given in the Maxwell stress tensor section of the electrostatic monograph.
and is used here. An electrostatic example is given in the Maxwell stress tensor section of the electrostatic monograph.
In the next example, the horseshoe magnet of the overview example will be modeled again, but now the magnetostatic force on the coin will be computed.
To correctly compute the ![]() component of the force on the iron coin at the iron-air interface, one needs to prioritize the air values over the iron values.
component of the force on the iron coin at the iron-air interface, one needs to prioritize the air values over the iron values.
The fields that generate these forces on the coin are those surrounding the coin body. So, to correctly compute the forces, it is necessary to know the values of the fields on the surface enclosing the coin body, which are the values in the domain's air side.
The region of interest is the coin, and it is here, where the surface integral of the Maxwell stress tensor will be computed:
To perform the integral, the boundary unit normals to the surfaces need to be computed.
Next, using the following formula derived above
the ![]() component to the Maxwell stress tensor is set up.
component to the Maxwell stress tensor is set up.
The integration gives a value of around 0.06 [![]() ], which corresponds to the value of one quarter of the coin. The actual force on the coin is therefore four times this value.
], which corresponds to the value of one quarter of the coin. The actual force on the coin is therefore four times this value.
Convergence of Magnetostatics Models
Typically, when an electromagnetic simulation is to be performed, the device of interest is surrounded by a second domain representing the material in which the device is embedded. This surrounding region repents an infinite domain around the device. Since an infinite domain cannot be modeled numerically, the domain needs to be truncated at some distance. An important question is then, How large should the surrounding domain be?
To decide how large the surrounding volume must be, one needs to perform a convergence test with respect to the surrounding domain size. In other words, one compares a quantity such as the magnetic energy generated by the magnet against the size of the surrounding volume. When the magnetic energy approaches a steady value, then the domain size no longer needs to be increased. To see the convergence of the value, a simple plot can be created.
In the next example, a convergence test will be performed for the cylindrical magnet overview example.
To perform the convergence test, it is necessary to change the size of the surrounding sphere, so in this case, a list of different radii will be defined.
Next, a parametric study will be conducted. The changing parameter is the radius, and as a consequence, there will be a different mesh for each radius. The PDE model will be solved for each radius.
A MagneticPotentialCondition will be used at the exterior boundaries with a default value of one. The exterior boundaries of the sphere are represented by point element marker with ID 1.
To compute the magnetic energy, the magnetic field intensity and the magnetic flux density need to be computed.
To compute the energy expression, ![]() , a mesh is required.
, a mesh is required.
In this case, the magnetostatic energy associated with the magnet will be computed. So, only the magnet region will be required.
The absolute value was used to find the energy associated solely with the magnet. The negative sign obtained indicated the direction of ![]() relative to
relative to ![]() .
.
The plot shows a steady value has been reached at about ![]() .
.
Boundary Conditions
Boundary conditions for magnetic models fall into one of two categories. Dirichlet conditions specify the magnetic scalar potential at boundaries. The other category involves boundaries that specify the value of the normal component of the magnetic flux density ![]() . These boundaries are realized with Neumann value boundary conditions.
. These boundaries are realized with Neumann value boundary conditions.
For every model, at least one magnetic potential boundary condition must be specified to make the differential equation solvable.
In addition to these two types of boundary conditions, there is also a third type, known as periodic boundary conditions, which are useful when the geometry has repetitive sections.
For the magnetostatic formulation, the following boundary conditions are introduced:
Next, these common boundary conditions are presented and explained. To keep things simple, the same base model is used in the subsequent examples. The model consists of an iron cube in a homogeneous magnetic field of ![]() [
[![]() ] directed along the
] directed along the ![]() axis. The model is shown in the figure below, where the grey cube represents the iron cube and the blue arrows the magnetic field.
axis. The model is shown in the figure below, where the grey cube represents the iron cube and the blue arrows the magnetic field.
On the left: an iron cube inside an homogeneous magnetic field directed in the positive ![]() axis. On the right: 1/8 of the domain.
axis. On the right: 1/8 of the domain.
The domain is composed of an iron cube of length ![]() [
[![]() ] and, due to symmetry, only 1/8 of the whole domain is simulated. The air boundary surrounding the iron cube is another a cube of length
] and, due to symmetry, only 1/8 of the whole domain is simulated. The air boundary surrounding the iron cube is another a cube of length ![]() [
[![]() ].
].
The magnetic field is antisymmetric to the ![]() plane and symmetric to the other planes. These planes are represented as boundaries in the model.
plane and symmetric to the other planes. These planes are represented as boundaries in the model.
Region markers will be employed to specify the material parameters of the iron and air regions.
The parameters to be used are the permeability of vacuum ![]() and iron
and iron ![]() and the flux density value of the magnetic field.
and the flux density value of the magnetic field.
All common boundary conditions used in magnetostatics can be shown with this model: a magnetic scalar potential, a magnetic flux density, a background magnetic flux density and symmetry boundary conditions. These conditions will be explained in the subsequent sections.
Magnetic Potential Boundary Condition
The purpose of a magnetic potential boundary condition is to set a specific scalar potential on some part of the boundary.
If the "MagneticPotential" is omitted a potential of 0 is used.
MagneticPotentialCondition returns a DirichletCondition. Predicates can be specified in exactly the same way as for DirichletCondition.
In the following example the use of MagneticPotentialCondition will be shown.
MagneticPotentialCondition example
A zero magnetic scalar potential condition is used to account for the antisymmetry at ![]() , where the magnetic field needs to be perpendicular to the boundary. A zero magnetic scalar potential condition is equivalent to an antisymmetry boundary condition.
, where the magnetic field needs to be perpendicular to the boundary. A zero magnetic scalar potential condition is equivalent to an antisymmetry boundary condition.
The plot illustrates the distribution of the magnetic scalar potential on the ![]() plane. The potential ranges from
plane. The potential ranges from ![]() [
[![]() ] to
] to ![]() [
[![]() ]. At
]. At ![]() the imposed MagneticPotentialCondition sets the potential to 0.
the imposed MagneticPotentialCondition sets the potential to 0.
Magnetic Flux Density Boundary Condition
The purpose of a magnetic flux density boundary condition is to define an inward or outward magnetic flux density at a boundary.
For simplicity, but without any restriction to generality, boundary condition equations will be presented in terms of the relative permeability ![]() . However, boundary condition equations can be used equally well for other equations shown in the Modeling magnetic materials section.
. However, boundary condition equations can be used equally well for other equations shown in the Modeling magnetic materials section.
With a prescribed scalar magnetic flux density ![]() [
[![]() ] normal to the boundary
] normal to the boundary ![]() , the magnetic flux density boundary condition is given by:
, the magnetic flux density boundary condition is given by:
A boundary where a magnetic flux density ![]() normal to the boundary is specified and not equal to zero is called a magnetic flux density boundary:
normal to the boundary is specified and not equal to zero is called a magnetic flux density boundary:
By convention, a negative sign is added in front of ![]() to indicate that the magnetic flux density is specified opposite to the outward boundary normal
to indicate that the magnetic flux density is specified opposite to the outward boundary normal ![]() . Therefore, a positive value denotes an inward magnetic flux density, and a negative value denotes an outward magnetic flux density.
. Therefore, a positive value denotes an inward magnetic flux density, and a negative value denotes an outward magnetic flux density.
Inserting ![]() into the constitutive law
into the constitutive law ![]() , a relation between the magnetic flux density
, a relation between the magnetic flux density ![]() and the magnetic scalar potential gradient
and the magnetic scalar potential gradient ![]() is obtained:
is obtained:
Inserting Eqn. 15 into Eqn. 16 gives ![]() .
.
MagneticFluxDensityValue returns a NeumannValue. Predicates can be specified in exactly the same way as for NeumannValue.
With a boundary magnetic flux density vector ![]() [
[![]() ] and boundary unit normal
] and boundary unit normal ![]() , the boundary condition is given by:
, the boundary condition is given by:
where ![]() is the magnetic flux density field at the boundary. The normal
is the magnetic flux density field at the boundary. The normal ![]() is automatically added and is computed using BoundaryUnitNormal. BoundaryUnitNormal represents an outward-pointing unit normal vector
is automatically added and is computed using BoundaryUnitNormal. BoundaryUnitNormal represents an outward-pointing unit normal vector ![]() on a region.
on a region.
If the magnetic flux density is specified as a vector of zeros or the normal component is specified with a zero value, then there is no flux density at that boundary. This is equivalent to a Neumann zero boundary condition. The magnetic insulation boundary condition is the implicit default boundary condition used if no other boundary condition is specified at a given boundary:
MagneticFluxDensityValue also can be used to model an background magnetic flux density boundary condition. The background magnetic flux density section shows this in detail.
In the following example, the use of MagneticFluxDensityValue will be shown.
MagneticFluxDensityValue example
To specify the homogeneous magnetic field across the domain, an outward magnetic flux density ![]() normal to the boundary, at
normal to the boundary, at ![]() , is specified.
, is specified.
Next, visualize the magnetic field ![]() .
.
The plot shows the direction and magnitude of the magnetic field intensity ![]() . The MagneticFluxDensityValue at
. The MagneticFluxDensityValue at ![]() generates the homogeneous magnetic field
generates the homogeneous magnetic field ![]() [
[![]() ] and forces it to flow in the positive
] and forces it to flow in the positive ![]() direction.
direction.
Symmetry Boundary Condition
A symmetry boundary condition is used when the computational domain and the expected magnetic scalar potential have mirror symmetry along an axis of the simulation domain.
The symmetry boundary condition is given by the dot product of ![]() and
and ![]() :
:
which states that the normal component of the magnetic field intensity is zero.
MagneticSymmetryValue returns a zero NeumannValue. So, a symmetry boundary condition is equivalent to an magnetic insulation boundary condition. If on some part of the boundary no boundary condition is specified, then a Neumann zero boundary condition is implicitly used.
MagneticSymmetryValue example
In the simplified geometry, at the surfaces parallel to the planes ![]() -
-![]() and
and ![]() -
-![]() , a symmetry boundary condition needs to be applied.
, a symmetry boundary condition needs to be applied.
On the left: an iron cube inside an homogeneous magnetic field directed along the ![]() axis. On the right: 1/8 of the whole domain.
axis. On the right: 1/8 of the whole domain.
A magnetic symmetry boundary condition is used to force the magnetic field to be tangential to the boundaries at the symmetry planes.
Since the magnetic symmetry condition is a Neumann zero boundary condition and is the default, it can be left out.
Next, visualize the magnetic field ![]() in the geometry used and in its mirrored geometry.
in the geometry used and in its mirrored geometry.
To visualize the other half of the field, at ![]() , the symmetric behavior of the field must be considered. At positive
, the symmetric behavior of the field must be considered. At positive ![]() values, the field is
values, the field is ![]() , and at negative
, and at negative ![]() values, the field is also
values, the field is also ![]() .
.
The plot shows the direction and magnitude of the magnetic field intensity ![]() at the original geometry and at the symmetry geometry, for
at the original geometry and at the symmetry geometry, for ![]() . The MagneticSymmetryValue forces the magnetic field to be tangential to the boundaries at the symmetry planes.
. The MagneticSymmetryValue forces the magnetic field to be tangential to the boundaries at the symmetry planes.
Antisymmetry Boundary Condition
An antisymmetry boundary condition models a boundary where a function ![]() being considered exhibits an antisymmetry with respect to an axis or plane. This means that the physical quantity of interest, such as the magnetic field, is mirrored across a boundary with a change in sign.
being considered exhibits an antisymmetry with respect to an axis or plane. This means that the physical quantity of interest, such as the magnetic field, is mirrored across a boundary with a change in sign.
The antisymmetry boundary condition is given by the cross product of ![]() and
and ![]() :
:
and is fulfilled if the potential ![]() is set to a constant at
is set to a constant at ![]() , due to the fact that the gradient of a constant potential is zero:
, due to the fact that the gradient of a constant potential is zero:
A magnetic potential boundary condition set to zero ![]() can be used as an antisymmetry boundary condition.
can be used as an antisymmetry boundary condition.
It is important to understand that an antisymmetry boundary condition forces the tangential component of the magnetic field to be zero at the plane of antisymmetry, resulting in the field having only a normal component. And in addition, across the antisymmetry boundary, the normal component to the boundary changes sign.
For example, if a magnetic field configuration is antisymmetric about the ![]() -
-![]() plane, then if the field component in the
plane, then if the field component in the ![]() direction at
direction at ![]() is
is ![]() , it will be
, it will be ![]() at
at ![]() .
.
Antisymmetry boundary condition example
In this simplified geometry, the magnetic field exhibits symmetry to the ![]() -
-![]() and
and ![]() -
-![]() planes and antisymmetry to the
planes and antisymmetry to the ![]() -
-![]() plane.
plane.
One-eighth of the iron cube model inside an homogeneous magnetic field directed along the ![]() axis.
axis.
At the left and front boundary, in the ![]() -
-![]() and
and ![]() -
-![]() planes, respectively, a symmetry boundary condition is applied. This boundary will force the magnetic field to be tangential to the boundaries.
planes, respectively, a symmetry boundary condition is applied. This boundary will force the magnetic field to be tangential to the boundaries.
The antisymmetry boundary condition comes into play at the lower boundary, at the ![]() plane, where the magnetic field needs to be normal to the boundary.
plane, where the magnetic field needs to be normal to the boundary.
A magnetic antisymmetry boundary condition is used to force the magnetic field to be normal to the boundaries specified.
Next, visualize the magnetic field ![]() in the geometry used and in its mirrored geometry below the antisymmetry plane.
in the geometry used and in its mirrored geometry below the antisymmetry plane.
To visualize the other half of the field, at ![]() , the antisymmetric behavior of the field must be considered. At positive
, the antisymmetric behavior of the field must be considered. At positive ![]() values, the field is
values, the field is ![]() , and at negative
, and at negative ![]() values, the field is
values, the field is ![]() .
.
The plot shows the direction and magnitude of the magnetic field intensity ![]() at the original geometry and at the symmetry geometry for
at the original geometry and at the symmetry geometry for ![]() . Across the symmetry at
. Across the symmetry at ![]() , the magnetic field exhibits an antisymmetric behavior. The antisymmetry boundary condition forces the magnetic field to be normal to the plane at
, the magnetic field exhibits an antisymmetric behavior. The antisymmetry boundary condition forces the magnetic field to be normal to the plane at ![]() , and the magnetic field is mirrored across the plane with a change in sign in the normal component,
, and the magnetic field is mirrored across the plane with a change in sign in the normal component, ![]() .
.
Periodic Boundary Condition
The purpose of a periodic boundary condition is to map the magnetic scalar potential from one boundary to another in order to model periodicity of the domain.
Given a function ![]() that maps the magnetic scalar potential
that maps the magnetic scalar potential ![]() from the periodic boundary
from the periodic boundary ![]() to the targeted boundary
to the targeted boundary ![]() , the periodic boundary condition can be written as:
, the periodic boundary condition can be written as:
Conditions at Material Interfaces
Maxwell's equations are valid for continuous material. However, in electromagnetics, it is common for electric or magnetic fields to be generated in one medium and transmitted to a second medium with different physical properties. The interface between any two materials is a physical discontinuity in the materials. The question then is, How are Maxwell equations solved in a multimaterial domain?
In the multimaterial case, the electromagnetics field quantities, of course, adhere to the physics at these material interfaces. These interface conditions are not boundary conditions that must be applied but conditions that provide the mathematical legitimacy to use the finite element method to solve the equations.
At a material interface separating two different materials the following conditions must be satisfied:
where ![]() [
[![]() ] is a surface current density deposited at the interface of medium 1 and medium 2. Eqn. 17 can be written as follows:
] is a surface current density deposited at the interface of medium 1 and medium 2. Eqn. 17 can be written as follows:
which means that the normal component of the magnetic flux density is continuous.This condition is equivalent to the natural boundary condition, discussed in the Magnetic flux density boundary condition section and hence is automatically satisfied.
On the other hand, the normal component of the magnetic field intensity will not be continuous. To show this, substitute ![]() :
:
showing that the normal component of ![]() must be discontinuous at the interface boundary. Since the permeability in the two materials
must be discontinuous at the interface boundary. Since the permeability in the two materials ![]() ; the only way that
; the only way that ![]() is true is when fields
is true is when fields ![]() and
and ![]() are discontinuous.
are discontinuous. ![]() must be discontinuous at the material interface.
must be discontinuous at the material interface.
Eqn. 18 means that the tangential component of the magnetic field intensity will be discontinuous if a surface current density is placed deliberately at the interface. If not, then the magnetic field intensity will be continuous across the interface:
On the other hand, substituting ![]() by
by ![]() , the following equation is deduced:
, the following equation is deduced:
These interface conditions have a direct consequence on the main variable being solved for, especially in models involving different media. At the interface, the magnetic scalar potential ![]() needs to satisfy the following conditions:
needs to satisfy the following conditions:
where ![]() is the normal derivative.
is the normal derivative.
These conditions are known in literature as the continuity conditions. These conditions essentially legitimate the use of the finite element method for electromagnetic computations, because these conditions are naturally satisfied with the finite element method. In other words, no additional measures need to be taken; the finite element method will automatically handle this.
Nomenclature
References
1. Blinder, S. M. (2011, March 7). "Magnetic Hysteresis." Wolfram Demonstrations Project. Retrieved from http://demonstrations.wolfram.com/MagneticHysteresis
2. Cardoso, J. R. (2018). Electromagnetics through the Finite Element Method. Boca Raton: CRC Press.
3. Domke, H.-J. (2011, March 7). "A Simple Model of Magnetization." Wolfram Demonstrations Project. Retrieved from http://demonstrations.wolfram.com/ASimpleModelOfMagnetization
4. Griffiths, D. J. (2017). Introduction to Electrodynamics (4th ed.). Cambridge University Press.
5. Gutfleisch, O., Willard, M. A., Brück, E., Chen, C. H., Sankar, S. G. and Liu, J. P. (2011). "Magnetic Materials and Devices for the 21st Century: Stronger, Lighter, and More Energy Efficient." Advanced Materials, 23(7), pp. 821–842.
6. Ida, N. and Bastos, J. P. (2013). Electromagnetics and Calculation of Fields. Springer Science & Business Media.
7. Kumar, S. and Tummuru, T. (2016, December). "Jiles-Atherton Model of Magnetic Hysteresis." Wolfram Demonstrations Project. Retrieved from https://demonstrations.wolfram.com/JilesAthertonModelOfMagneticHysteresis
8. Mesquita, R. C. and Bastos, J. P. A. (1992). "An Incomplete Gauge Formulation for 3D Nodal Finite-Element Magnetostatics." IEEE Transactions on Magnetics, 28(2), pp. 1044–1047.
9. Purcell, E. M. (2013). Electricity and Magnetism. Cambridge University Press.