AffineStateSpaceModel[{a,b,c,d},x]
アフィン型の状態空間モデル ![]() ,
, ![]() を表す.
を表す.
系のモデル sys に対応するアフィン型の状態空間モデルを与える.
AffineStateSpaceModel[eqns,{{x1,x10},…},{{u1,u10},…},{g1,…},t]
出力 gi,独立変数 t である微分方程式 eqns の xi0における従属変数 xiと uj0における入力 ujについてのテイラー(Taylor)入力線形化で得られた状態空間モデルを与える.


AffineStateSpaceModel
AffineStateSpaceModel[{a,b,c,d},x]
アフィン型の状態空間モデル ![]() ,
, ![]() を表す.
を表す.
系のモデル sys に対応するアフィン型の状態空間モデルを与える.
AffineStateSpaceModel[eqns,{{x1,x10},…},{{u1,u10},…},{g1,…},t]
出力 gi,独立変数 t である微分方程式 eqns の xi0における従属変数 xiと uj0における入力 ujについてのテイラー(Taylor)入力線形化で得られた状態空間モデルを与える.
詳細とオプション



- AffineStateSpaceModelは,入力線形モデルとしても知られている.
- AffineStateSpaceModelは,制御入力がアフィン型で起るが,それでも高度な解析および制御設計を許容するような任意の系を表すことができる.
- 次の短縮入力形を使うことができる.
-
AffineStateSpaceModel[{a,b,c},x] 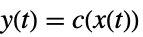 によって与えられる出力
によって与えられる出力AffineStateSpaceModel[{a,b},x] 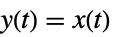 によって与えられる出力
によって与えられる出力 - AffineStateSpaceModel[{a,b,…},x,u,y,t]は,入力変数 u,出力変数 y,独立変数 t を明示的に指定する.
- AffineStateSpaceModelでは,状態 x と入力 u の動作値を使うことができる.
- AffineStateSpaceModel[…,{{x1,x10},…},{{u1,u10},…},…]を使って系の動作値を示すことができる. »
- AffineStateSpaceModel[sys]では,次の系を変換することができる.
-
NonlinearStateSpaceModel 近似テイラー変換 StateSpaceModel 厳密変換 TransferFunctionModel 厳密変換 - 状態方程式
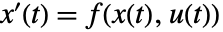 および出力方程式
および出力方程式 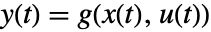 を持つ常微分方程式系は,
を持つ常微分方程式系は,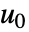 において線形化される.
において線形化される. - 入力線形化系は,状態
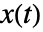 ,入力
,入力 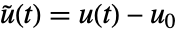 ,出力
,出力 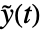 を持つ.状態方程式は
を持つ.状態方程式は 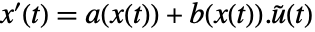 ,出力方程式は
,出力方程式は 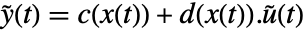 である.係数関数は
である.係数関数は 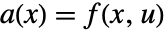 ,
,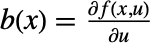 ,
,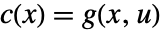 ,
,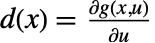 で与えられる.すべてが
で与えられる.すべてが 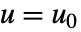 で評価される.
で評価される. - 状態方程式
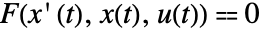 ,出力方程式
,出力方程式 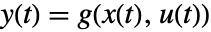 を持つ微分代数方程式系は,
を持つ微分代数方程式系は,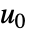 において線形化される.
において線形化される. - 入力線形化系は,状態
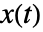 ,入力
,入力 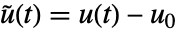 ,出力
,出力 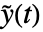 を持つ.状態方程式は
を持つ.状態方程式は 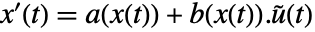 ,出力方程式は
,出力方程式は 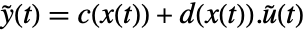 である.係数関数は
である.係数関数は 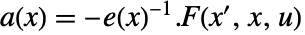 ,
,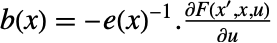 ,
,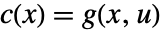 ,
,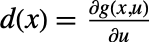 ,
,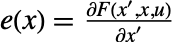 で与えられる.すべてが
で与えられる.すべてが 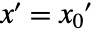 および
および 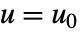 で評価される.
で評価される. - 状態および入力のより高次の導関数を含む微分方程式は,追加的な状態を導入することで,上記のケースに簡約される.
- 操作点 xi0および uj0がAutomaticである計算では,OutputResponse等の関数ではこれがゼロであると仮定され,ControllableModelQのような関数では,これがStateSpaceModelへの変換,あるいは一般的であると仮定される.
- AffineStateSpaceModel[…]["prop"]は,特性"prop"の値を与える.
- AffineStateSpaceModel[…]["Properties"]は,使用可能な特性のリストを与える.
- 次は,使用可能なオプションである.
-
Appearance Automatic モデルの外観 ExternalTypeSignature Automatic 埋め込まれたコードの変数型 SamplingPeriod Automatic サンプリング周期 SystemsModelLabels Automatic 変数のラベル - オプションAppearanceは,Automatic,"Detailed","Structured","Elided","Iconized"の値を取ることができる.
- AffineStateSpaceModelは,OutputResponseおよびSystemsModelSeriesConnectの関数で使うことができる.
例題
すべて開く すべて閉じるスコープ (31)
基本的な用法 (5)
StateSpaceModelを得るためにテイラー線形化を用いる:
系の変換 (6)
StateSpaceModelのアフィン表現:
TransferFunctionModelのアフィン表現:
NonlinearStateSpaceModelのテイラー入力線形化:
アフィン型のモデルは厳密にNonlinearStateSpaceModelとして表現される:
モデル操作 (5)
動作値 (10)
SystemsModelDeleteを使って削除された状態と入力は,それぞれの動作値に設定される:
SystemsModelExtractによって抽出されなかった状態と入力も同様である:
StateSpaceTransformは,もとの状態の動作値が指定されている場合は,新たな状態の動作値を計算する:
デフォルトで,シミュレーション関数は動作値を初期値と想定する:
StateSpaceModelは動作値について線形化する:
動作値はNonlinearStateSpaceModelへの変換に保存される:
FullInformationOutputRegulatorは,ゲイン ![]() を計算するために動作値周辺で線形化を行う:
を計算するために動作値周辺で線形化を行う:
動作値 ![]() が与えられている場合は,ControllableModelQ は
が与えられている場合は,ControllableModelQ は ![]() から可制御性を検定する:
から可制御性を検定する:
ControllableDecompositionも同様に動作する:
動作値 ![]() が与えられている場合は,ObservableModelQ は
が与えられている場合は,ObservableModelQ は ![]() における可観測性を検定する:
における可観測性を検定する:
ObservableDecompositionも同様な動作を示す:
FeedbackLinearizeは動作値において線形化する:
デフォルトで,始点で線形化が行われるが,このことは場合によっては問題を生む:
特性 (5)
オプション (4)
アプリケーション (18)
機械系 (9)
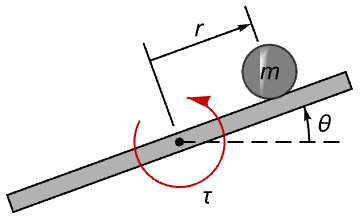
回転運動 ![]() (トルク = 慣性 x 角加速度)というニュートンの方程式からの振子をモデル化する:
(トルク = 慣性 x 角加速度)というニュートンの方程式からの振子をモデル化する:
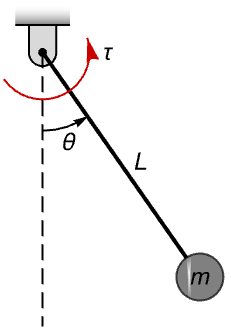
この方程式は適用されるトルクの入力 ![]() についてアフィン方程式である:
についてアフィン方程式である:
以下の球状振子を,そのラグランジュ方程式 ![]() と一般化座標
と一般化座標 ![]() および
および ![]() でモデル化する:
でモデル化する:
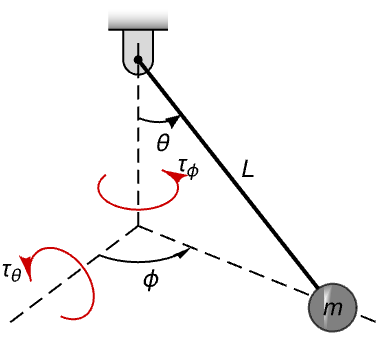
この方程式はアフィン方程式でありAffineStateSpaceModelで厳密に表現される:
二重振子を,そのハミルトン方程式 ![]() でモデル化する.ただし,
でモデル化する.ただし,![]() は一般化座標,
は一般化座標,![]() は一般化運動量であり,
は一般化運動量であり,![]() はそのラグランジュ方程式である:
はそのラグランジュ方程式である:
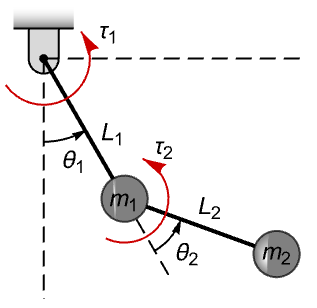
振子の初期角度40°で閉ループ系のパフォーマンスを評価する:
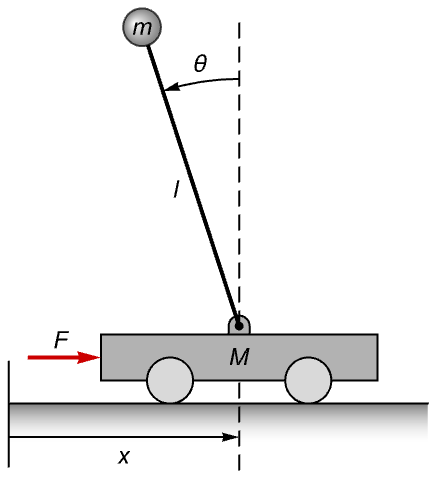
梁の上でバランスを保っているボールをモデル化する.梁の角度 ![]() だけですべての内部状態が観察できるかどうかを求める:
だけですべての内部状態が観察できるかどうかを求める:
制御入力を運転速度と操縦角度率として,自動車の運動学をモデル化する.自動車の横への動きは制御入力を組み合せることで制御可能であることを示す:
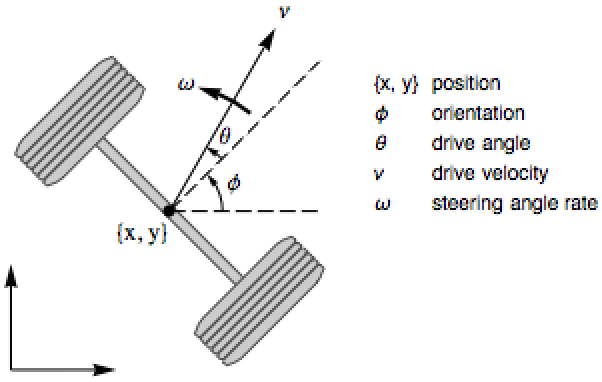
運転速度 ![]() ,操縦角度率
,操縦角度率 ![]() が入力なので,このモデルにはダイナミクスはない:
が入力なので,このモデルにはダイナミクスはない:
AffineStateSpaceModelは,自動車が全方向に可制御であることを示している:
駆動力 ![]() ,トルク
,トルク ![]() を入力として,橇の水平面における可制御性:
を入力として,橇の水平面における可制御性:
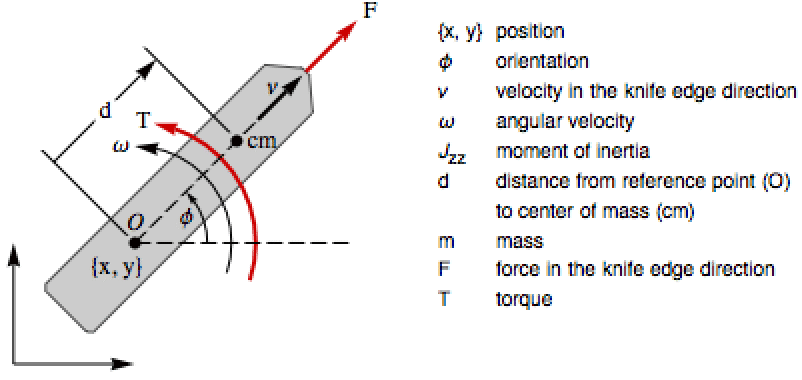
平面垂直離陸着陸 (PVTOL) 航空機のゼロダイナミクスを計算する:»
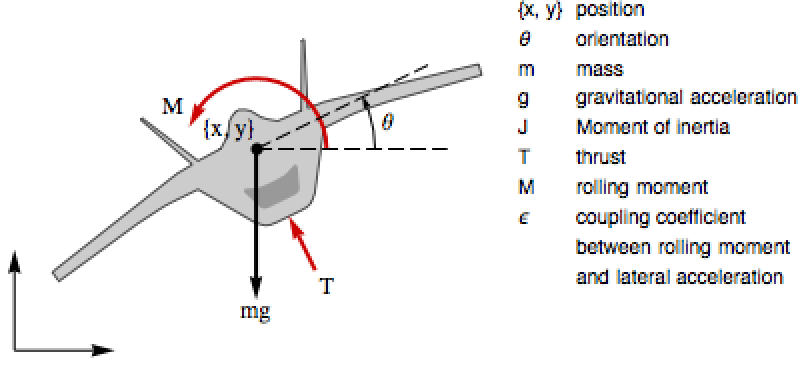
電気系 (4)
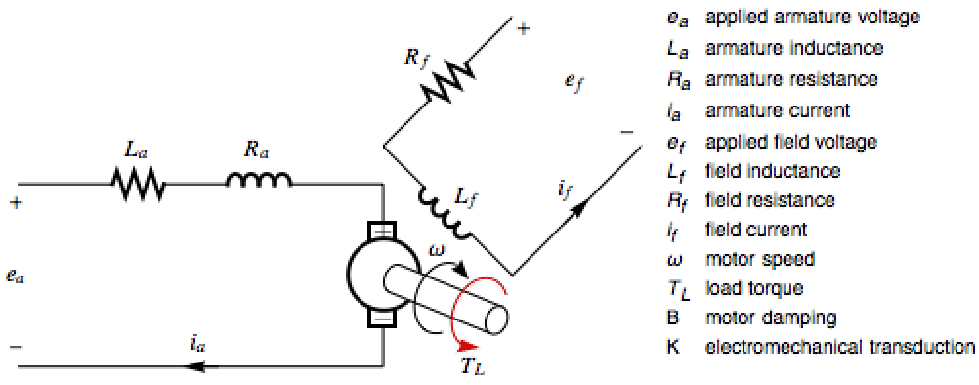
電機子電圧,界磁電圧,負荷トルクを入力として,別々に励起された直流モーターをモデル化し,線形近似の極における減衰の影響を見る:»
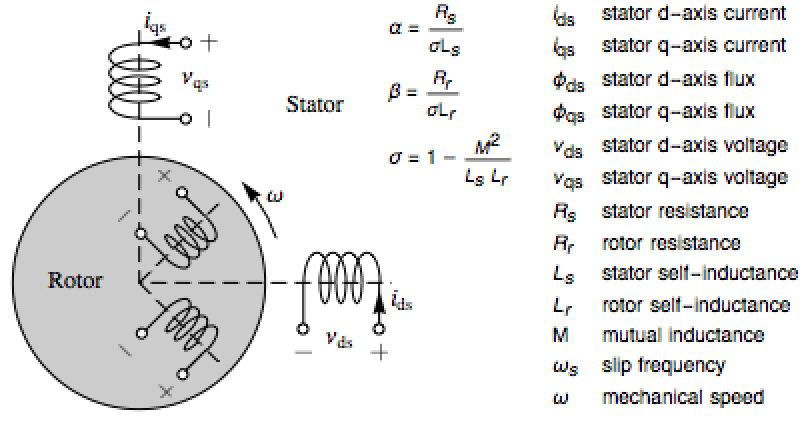
dq回転座標における誘導電動機をモデル化し,これを使って位相座標を出力として持つモデルを得る:»
一般化された座標と擬似速度の関係を表す運動方程式およびポアンカレ(Poincaré)の方程式として得られる動的方程式使って,3位相シンクロナスモーターのモデルを組み立てる.入力は負荷トルク ![]() ,Blondel電圧
,Blondel電圧![]() ,巻線
,巻線 ![]() である:»
である:»
生成された座標は,ローターの角度,固定子の巻電荷,場の巻電荷である:
擬似速度は角速度,Blondel電流,界磁電流として選ばれる:
一般化された力は ![]() として計算される.ただし,
として計算される.ただし,![]() はLurのポテンシャル関数である:
はLurのポテンシャル関数である:
ラグランジュ![]() ,構造係数
,構造係数 ![]() ,一般化された力
,一般化された力 ![]() から,ポアンカレの方程式
から,ポアンカレの方程式![]() を組み立てる:
を組み立てる:
運動方程式およびポアンカレの方程式からアフィンモデルを得ることができる:
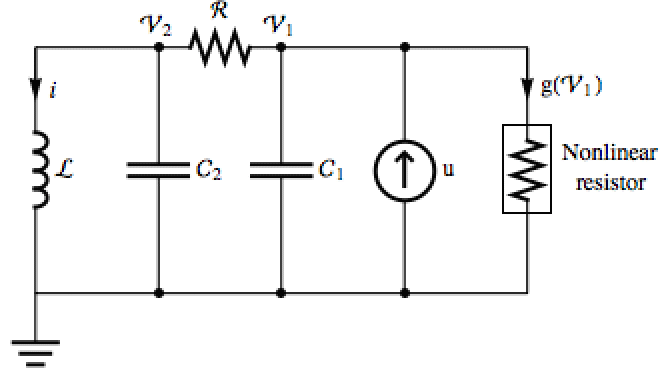
さまざまな非線形特性について,Chuaの回路のシミュレーションを行う:»
化学系 (5)
連続発酵槽における化学反応について,アフィン型のモデルと線形モデルのシミュレーションを比較する:»

入力 ![]() ,状態
,状態 ![]() ,出力
,出力 ![]() (のモデルを指定する.これは生産性のモデルである:
(のモデルを指定する.これは生産性のモデルである:
バイオマスと基質のある種の初期濃度から始めて,生産性のシミュレーションを行う:
このシミュレーションによると,非線形動作が線形化された動作と著しく異なることが分かる:
周波数法を用い,非等温連続撹拌層反応器 (CSTR) 内の反応について,アフィンモデルと線形モデルを比較する:»
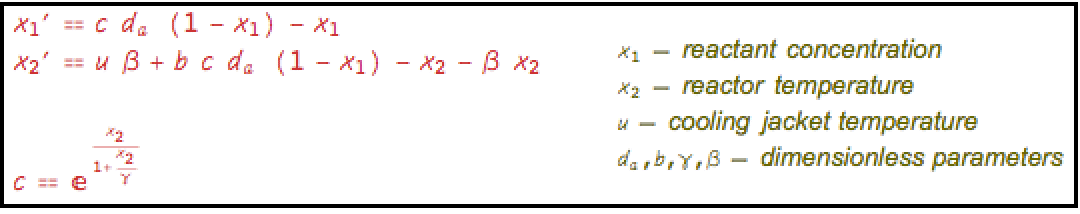
始点周囲のテイラー線形化でTransferFunctionModelを得る:
BodePlotは,線形系の周波数応答を与える:
周波数1におけるゲインの減衰と位相遅れは,座標を読むことで得られる:
このプロットは,アフィン系にはそれほど減衰が見られないが,線形化された系による予想よりも位相遅れが大きいことを示している:
等温CSTR内の,反応 ![]() のゼロダイナミクスを得る:»
のゼロダイナミクスを得る:»
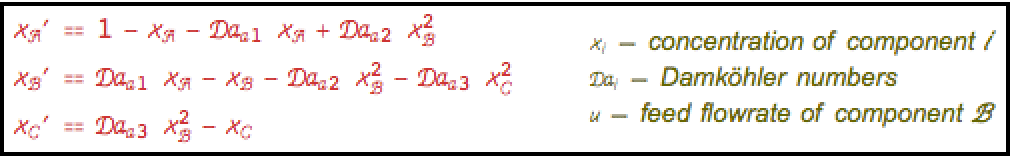
厳密な線形化を使い,シクロペンタノール合成過程 ![]() ,
,![]() での
での ![]() および
および ![]() の濃度を制御する制御器を設計する.ただし,
の濃度を制御する制御器を設計する.ただし,![]() はシクロペンタノール,
はシクロペンタノール,![]() はジシクロペンタジエンである:»
はジシクロペンタジエンである:»

ガスメタルアーク溶接過程は,アフィン系でモデル化することができる.指定されたアーク長を保つことができるフィードバック法則を設計する:»
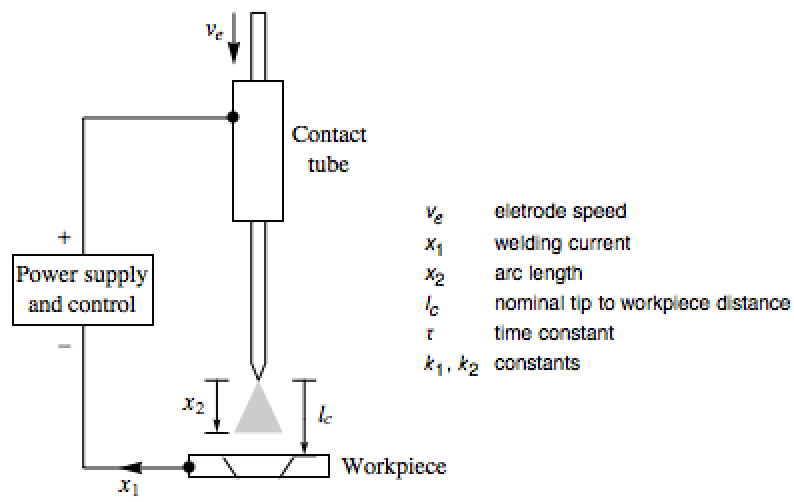
アーク長を1センチに保つようにAsymptoticOutputTrackerを使ってフィードバック法則を計算する:
特性と関係 (4)
状態と入力の線形化でAffineStateSpaceModelをStateSpaceModelに変換する:
入力の線形化でNonlinearStateSpaceModelをAffineStateSpaceModelに変換する:
状態と入力の線形化でTransferFunctionModelに変換する:
考えられる問題 (1)
Transposeを使ってそれらを列に並べる:
テキスト
Wolfram Research (2014), AffineStateSpaceModel, Wolfram言語関数, https://reference.wolfram.com/language/ref/AffineStateSpaceModel.html.
CMS
Wolfram Language. 2014. "AffineStateSpaceModel." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/AffineStateSpaceModel.html.
APA
Wolfram Language. (2014). AffineStateSpaceModel. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/AffineStateSpaceModel.html
BibTeX
@misc{reference.wolfram_2025_affinestatespacemodel, author="Wolfram Research", title="{AffineStateSpaceModel}", year="2014", howpublished="\url{https://reference.wolfram.com/language/ref/AffineStateSpaceModel.html}", note=[Accessed: 11-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_affinestatespacemodel, organization={Wolfram Research}, title={AffineStateSpaceModel}, year={2014}, url={https://reference.wolfram.com/language/ref/AffineStateSpaceModel.html}, note=[Accessed: 11-February-2026]}