ArcTan
詳細

- 記号操作・数値操作の両方に適した数学関数である.
- 答はラジアンで求まる.
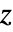 が実数のとき,答は必ず
が実数のとき,答は必ず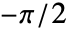 〜
〜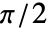 の範囲にある.
の範囲にある.- 特別な引数の場合,ArcTanは自動的に厳密値を計算する.
- ArcTanは任意の数値精度で評価できる.
- ArcTanは自動的にリストに関数の並列的な適用を行う.
- ArcTan[z]は,複素
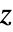 平面上,
平面上,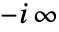 〜
〜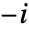 そして
そして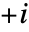 〜
〜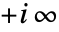 の範囲で不連続な分枝切断線を持つ.
の範囲で不連続な分枝切断線を持つ. 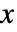 または
または 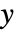 が複素数のとき,ArcTan[x,y]は,
が複素数のとき,ArcTan[x,y]は,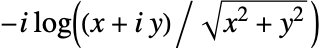 を意味する.
を意味する.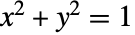 のときにArcTan[x,y]は,
のときにArcTan[x,y]は,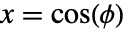 および
および 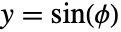 を満たす数
を満たす数 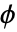 を見出す.
を見出す.- ArcTanはIntervalオブジェクトおよびCenteredIntervalオブジェクトに使うことができる. »
予備知識
- ArcTanは,逆正接関数である.実数 x については,ArcTan[x]は,
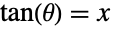 となるラジアン角度測定値
となるラジアン角度測定値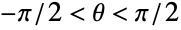 を表す.2つの引数を取る形式であるArcTan[x,y]は,点
を表す.2つの引数を取る形式であるArcTan[x,y]は,点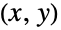 がある象限を考慮に入れて,y/x の逆正接を表す.このため,正の
がある象限を考慮に入れて,y/x の逆正接を表す.このため,正の 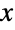 軸から測定された点の角度位置(ラジアンで表される)を返す.ArcTanは,直交座標系から極座標系に変換する場合に,またフェーザ表記
軸から測定された点の角度位置(ラジアンで表される)を返す.ArcTanは,直交座標系から極座標系に変換する場合に,またフェーザ表記 ![x+ⅈ y=TemplateBox[{z}, Abs]ⅇ^(ⅈ phi) x+ⅈ y=TemplateBox[{z}, Abs]ⅇ^(ⅈ phi)](Files/ArcTan.ja/24.png) の位相
の位相 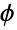 を求める場合に,便利である.
を求める場合に,便利である. - ArcTanは,自動的にリストに縫い込まれる.特別な厳密値の引数の場合,ArcTanは自動的に厳密値を計算する.引数として厳密な数式が与えられている場合には,ArcTanは任意の数値精度に評価してもよい.ArcTanを含む記号式の操作に有効な関数には,FunctionExpand,TrigToExp,TrigExpand,Simplify,FullSimplifyがある.
- ArcTanは,複素引数
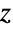 については,
については,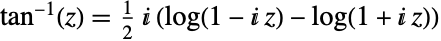 を通して定義される.
を通して定義される. - ArcTan[z]は,複素
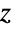 平面上に不連続な分枝切断線を持つ.関連する数学関数には,Arg,Tan,ArcCot,ArcTanh,Gudermannianがある.
平面上に不連続な分枝切断線を持つ.関連する数学関数には,Arg,Tan,ArcCot,ArcTanh,Gudermannianがある.
例題
すべて開くすべて閉じる例 (7)
スコープ (49)
数値評価 (6)
ArcTanを高精度で効率よく評価する:
IntervalオブジェクトとCenteredIntervalオブジェクトを使って最悪の場合に保証される区間を計算する:
Aroundを使って平均的な場合の統計区間を計算することもできる:
MatrixFunctionを使って行列のArcTan関数を計算することもできる:
特定の値 (6)
関数の特性 (12)
級数展開 (4)
積分変換 (3)
関数表現 (5)
アプリケーション (9)
有理関数の積分をArcTanについて求める:
ArcTanの分枝切断線は虚軸に沿っている:
双曲線正割の標準分布の累積分布関数(CDF)はArcTanによって与えられる:
これはGudermannian関数をスケールしてシフトしたものである:
特性と関係 (5)
FullSimplifyを使ってArcTanを含む式を簡約する:
ArcTanは角度をラジアンで与えるのに対し,ArcTanDegreesは同じ角度を度で与える:
ArcTanはいくつかの特殊関数の特別な場合である:
考えられる問題 (1)
ArcTanは多価関数であるので,![]() である:
である:
テキスト
Wolfram Research (1988), ArcTan, Wolfram言語関数, https://reference.wolfram.com/language/ref/ArcTan.html (2021年に更新).
CMS
Wolfram Language. 1988. "ArcTan." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2021. https://reference.wolfram.com/language/ref/ArcTan.html.
APA
Wolfram Language. (1988). ArcTan. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/ArcTan.html