AttentionLayer

AttentionLayer[]

表示一个可训练的网络层，学习注意其输入的某些部分.

AttentionLayer[net]

指定特定网络，为输入的某些部分打分.

AttentionLayer[net,opts]

包括权重归一化、屏蔽选项和其他参数.

更多信息和选项

  • AttentionLayer[net] 接受一组键向量、一组值向量以及一个或多个查询向量，用来自 net[<|"Input"key,"Query"query|>] 的 softmax 归一化的分数计算每个查询向量的值向量的加权和.
  • 在其一般的单标头形式中，AttentionLayer[net] 接受一个维度为 d1×…×dn×k 的键值数组 K，一个维度为 d1×…×dn×v 的值数值 V，和一个维度为 q1×…×qm×q 的查询数组 Q. 键和值数组可以被视为尺寸为 d1×…×dn、元素为向量的数组. 对于 K，这些向量用 k 表示，尺寸为 k，对于 V，这些向量用 v 表示，尺寸为 v. 相似地，查询数组可以被视为尺寸为 q1×…×qm、元素为用 q 表示的向量、尺寸为 q 的数组. 注意，如果 m 为 0，则查询数组可以是尺寸为 q 的单一查询向量. 然后，计分网络 f 用于计算每一种 d1×…×dn 键向量 k 和 q1×…×qm 查询向量 q 组合的标量分数， s=f(k,q). 这些标量分数用于生成尺寸为 q1×…×qm、含有加权和 o=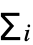wivi 的输出数组 O，其中权值为 w=softmax(S)，且 S 是为给定查询向量生成的 d1×…×dn 标量分数数组.
  • AttentionLayer[net] 的一个常见应用是，当键为 n×k 矩阵时，值是 n×v 矩阵，查询时尺寸为 q 的单一向量. AttentionLayer 将计算单一输出向量 o，该输出向量是 n-值行向量的加权和： o=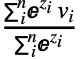，其中 zi=f(ki,q). 在Wolfram 语言中，这可以写作 Total[values*weights]，其中 weights 为SoftmaxLayer[][Map[net[<|"Input"#,"Query"query|>]&,keys]].
  • 在 AttentionLayer[net] 中，打分网络 net 可为以下任一形式：
  • "Dot"计算 s=Dot[k,q] 的 NetGraph
    "Bilinear"计算 s=Dot[k,W,q] 的 NetGraph，其中 W i是一个可学习的矩阵（默认）
    NetGraph[…]特定的 NetGraph，接受 "Input" 和 "Query" 矢量，产生标量 "Output" 值
  • 可包含以下可选参数：
  • "Dropout" 0注意力权重的丢弃率
    LearningRateMultipliers Automatic计分网络的学习率乘数
    "Mask" None防止某种注意力模式
    "MultiHead" False是否执行多头注意力，其中倒数第二个维度对应于不同的关注头
    "ScoreRescaling" None用来缩放分数的方法
  • "Mask" 的可能设置有：
  • None无掩蔽
    "Causal"因果掩蔽
    "Causal"n具有大小为 n 的窗口的局部因果掩蔽
  • 指定 "Dropout"p 以概率 p 对注意力权重应用丢弃，其中 p 是 0 到 1之间（包含 0 且不包括 1）之间的标量.
  • 在设置为 "Mask""Causal" 的情况下，查询输入被限制为与键和值输入具有相同长度的向量序列，只有位置满足 t'<t 的键和值输入被用来计算位置 t 处的输出.
  • 使用 "Mask""Causal"n 设置，其中 n 是一个正整数，只有键的位置 t-n<t'<=t 和值输入用于计算位置 t 的输出.
  • 当设置为 "MultiHead"True 时，键和值输入的秩必须至少为三，查询输入的秩必须至少为二，并且所有输入的倒数第二个维度都应相同，表示关注头的数量. 每个关注头对应一个不同的关注机制，并且所有关注头的输出都被合并在一起.
  • 当设置为 "ScoreRescaling""DimensionSqrt" 时，在被 softmax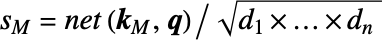： 归一化之前，将分数除以键的输入维度的平方根.
  • AttentionLayer 通常被用在 NetGraph 中.
  • AttentionLayer 开放以下输入端口以便用在 NetGraph 等中：
  • "Key"大小为 d1×…×dn×k 的数组（或具有多头注意力时，大小为 d1×…×dn×h×k 的数组）
    "Value"大小为 d1×…×dn×v 的数组（或具有多头注意力时，大小为 d1×…×dn×h×k 的数组）
    "Query"大小为 q1×…×qm×q 的数组（或具有多头注意力时，大小为 q1×…×qm×h×k 的数组）
  • AttentionLayer 开放输出端口以便用在 NetGraph 等中：
  • "Output"尺寸为 q1×…×qm×v 的输出数组（或具有多头注意力时，大小为 q1×…×qm×h×v 的输出数组）
  • AttentionLayer 暴露额外端口访问内部注意力权重：
  • "AttentionWeights"维度为 d1×…×dn×q1×…×qm （或具有多头注意力 d1×…×dn×h×q1×…×qm）的权重数组
  • AttentionLayer[…,"Key"shape1,"Value"shape2,"Query"shape3] 允许指定输入的形式. shapei 的可能的形式包括：
  • NetEncoder[…]产生数组序列的编码器
    {d1,d2,…}维度为 d1×d2×… 的数组
    {"Varying",d1,d2,…}一个数组，其第一个维度可变，剩下的维度为 d2×d3×…
    {Automatic,…}一个数组，其维度将从推断而得
    {"Varying",Automatic,…}数量不定的数组，每个数组的大小将从推断而得
  • 通常在 NetGraph 中自动推断键、值和查询数组的大小.
  • AttentionLayer[…][<|"Key"key,"Value"value,"Query"query|>] 通过应用该层显式计算输出.
  • AttentionLayer[…][<|"Key"{key1,key2,…},"Value"{value1,value2,…},"Query"{query1,query2,…}|>] 在一批输入中显式计算每个 keyi、valuei 和 queryi 的输出.
  • AttentionLayer[…][input,NetPort["AttentionWeights"]] 可用于访问某些输入上的 softmax 归一化注意力权重.
  • 当 NumericArray 作为输入时，输出将是 NumericArray.
  • NetExtract[…,"ScoringNet"] 可用于提取 AttentionLayer[net] 对象的 net.
  • Options[AttentionLayer] 给出构造层的默认选项列表. Options[AttentionLayer[…]] 提供用于在某些数据上运算层的默认选项列表.
  • Information[AttentionLayer[…]] 提供有关该层的报告.
  • Information[AttentionLayer[…],prop] 给出 AttentionLayer[…]的属性 prop 的值. 可能的属性与 NetGraph 的属性相同.

范例

打开所有单元关闭所有单元

基本范例  (2)

创建一个 AttentionLayer：

创建一个随机初始化的 AttentionLayer，接受二维键序列、三维值序列和一维查询序列：

对输入应用该层：

该层逐项作用于一批不同长度的序列：

范围  (4)

打分网络  (2)

用 "Dot" 打分网络创建一个 AttentionLayer：

提取 "Dot" 打分网络：

创建一个新的 AttentionLayer，明确将打分网络指定为 NetGraph 对象：

创建一个具有可训练参数的自定义打分网络：

创建并初始化一个使用自定义打分网络的 AttentionLayer：

对一个查询矢量应用该层：

对查询序列应用该层：

注意力权重  (2)

创建一个 AttentionLayer：

计算给定输入的注意力权重：

在这种情况下，权重对应于：

计算层的注意力权重和输出：

使用基于 AttentionLayer 的模型：

该网络包含几个具有 12 个头部的多头自注意力层，例如：

对于给定的网络输入，提取该层的注意力权重：

将第一个注意力头部的权重表示为输入令牌之间的连接强度：

选项  (7)

"Dropout"  (1)

在注意力权重掩蔽上定义一个带有丢弃的 AttentionLayer：

如果没有特定训练的行为，该层会返回与没有丢弃相同的结果：

设置 NetEvaluationMode"Train"，则该层返回不同结果：

直接将丢弃应用于注意力权重：

LearningRateMultipliers  (1)

制作一个具有任意权重的打分网络：

在 AttentionLayer 中使用该打分网络，使用选项 LearningRateMultipliers 冻结其权重：

训练时，打分网络的权重将使用零学习率乘数：

"Mask"  (2)

使用因果掩蔽定义一个 AttentionLayer：

使用一个查询向量和长度为五的序列应用该注意力层：

给定步骤的输出仅取决于此步骤之前键和值. 要特别指出的是第一个输出矢量即第一个值矢量.

注意力权重形成一个下三角矩阵：

使用窗口尺寸为 3 的局部因果掩蔽定义一个 AttentionLayer：

使用一个查询向量和长度为五的序列应用该注意力层：

给定步骤的输出仅取决于最后三个步骤的键和值.

这可以在包含零的注意力权重矩阵中观察到：

"MultiHead"  (2)

定义一个具有两个头的 AttentionLayer：

对一个查询向量和长度为三的序列施加多头注意力：

结果与分别在每个头上施加单头注意力并联合结果相同：

定义一个 NetGraph 来执行六个头的多头自我注意力：

应用于长度为三的序列的 NumericArray：

"ScoreRescaling"  (1)

创建一个根据输入维度重新调整注意力分数的 AttentionLayer：

计算输入上的层：

与没有重新调整的分数相比，输出的对比没有那么强烈：

即使其顺序保持不变，注意力权重的对比也相对较小：

应用  (1)

要对数字列表进行排序，先生成由 1 到 6 之间的整数组成的列表构成的测试集和训练集：

显示从训练集中抽取的三个随机样本：

定义含有 AttentionLayer 的 NetGraph：

对网络进行训练：

用网络对整数列表进行排序：

属性和关系  (4)

如果查询、键和值输入时矩阵，那么，AttentionLayer[net] 计算：

定义一个 AttentionLayer 并提取打分子网络：

在一些测试数据上运行 AttentionLayer：

等价于：

AttentionLayer[net,"ScoreRescaling""DimensionSqrt"] 计算：

定义一个 AttentionLayer 并提取打分子网络：

在一些测试数据上运行 AttentionLayer：

等价于：

AttentionLayer[scorer,"Mask""Causal","ScoreRescaling""DimensionSqrt"] 计算：

定义一个 AttentionLayer 并提取打分子网络：

在一些测试数据上运行 AttentionLayer：

等价于：

如果 "Key" 和 "Value" 输入是一样的，AttentionLayer 等价于弃用的 SequenceAttentionLayer：

等价于：

可能存在的问题  (1)

当对 AttentionLayer[net] 中的打分网络 net 使用设置 "Dot" 时，输入键和查询矢量的大小必须相同：

使用同样的大小：

这项限制不适用于 "Bilinear" 打分网络：

Wolfram Research (2019)，AttentionLayer，Wolfram 语言函数，https://reference.wolfram.com/language/ref/AttentionLayer.html （更新于 2022 年）.

文本

Wolfram Research (2019)，AttentionLayer，Wolfram 语言函数，https://reference.wolfram.com/language/ref/AttentionLayer.html （更新于 2022 年）.

CMS

Wolfram 语言. 2019. "AttentionLayer." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2022. https://reference.wolfram.com/language/ref/AttentionLayer.html.

APA

Wolfram 语言. (2019). AttentionLayer. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/AttentionLayer.html 年

BibTeX

@misc{reference.wolfram_2024_attentionlayer, author="Wolfram Research", title="{AttentionLayer}", year="2022", howpublished="\url{https://reference.wolfram.com/language/ref/AttentionLayer.html}", note=[Accessed: 17-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_attentionlayer, organization={Wolfram Research}, title={AttentionLayer}, year={2022}, url={https://reference.wolfram.com/language/ref/AttentionLayer.html}, note=[Accessed: 17-November-2024 ]}