BilateralZTransform

BilateralZTransform[expr,n,z]

给出 expr 的双边 Z 变换..

BilateralZTransform[expr,{n1,…,nk},{z1,…,zk}]

给出 expr 的多维双边 Z 变换.

更多信息和选项

  • 双边 Z 变换是双边拉普拉斯变换的离散模拟，在数字信号处理等领域发挥着重要作用.
  • 离散函数 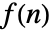的双边 Z 变换由 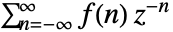给出.
  • 多维双边 Z 变换由 给出.
  • 如果第三个参数 z 被赋予一个数值，则使用数值方法计算总和.
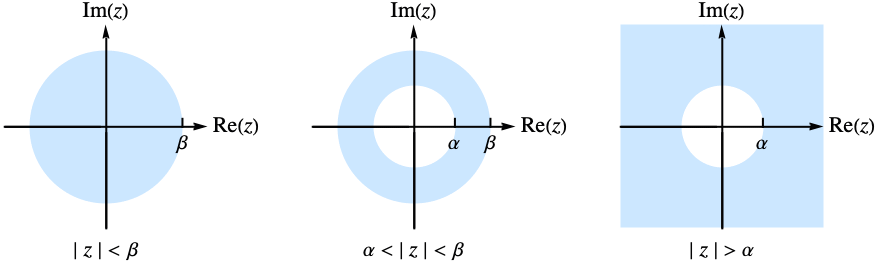
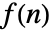  • 的双边 Z 变换仅对于由 alpha<TemplateBox[{z}, Abs]<beta 给出的环中 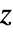的复数值存在. 在某些情况下，定义环可能会延伸到圆盘的外部或内部.
  • 可以提供以下选项：
  • AccuracyGoalAutomatic所追求的绝对精度的位数
    Assumptions $Assumptions关于参数要做的假设
    GenerateConditions True是否生成包含参数条件的答案
    MethodAutomatic要使用的方法
    PerformanceGoal$PerformanceGoal要最优化的性能方面
    PrecisionGoalAutomatic所追求的精度位数
    WorkingPrecision Automatic内部计算所用的精度

范例

打开所有单元关闭所有单元

基本范例  (2)

定义一个指数衰减序列：

计算其双边 Z 变换：

双边 Z 变换的复数图：

计算单个点的变换：

计算多元函数的双边 Z 变换：

范围  (8)

UnitStep 函数的双边 Z 变换：

离散幂函数：

幂函数的组合：

DiscreteDelta：

离散时间有限支持函数：

三角序列：

计算单个点的双边 Z 变换：

或者，以符号方式计算变换：

然后运算 的特定值：

对于某些函数，双边 Z 变换只能通过数值计算：

仅使用数值绘制双边 Z 变换：

选项  (3)

Assumptions  (1)

使用 Assumptions 指定参数的范围：

GenerateConditions  (1)

将 GenerateConditions 设置为 False 以获得无条件的结果：

WorkingPrecision  (1)

使用 WorkingPrecision 获得任意精度的结果：

应用  (2)

定义有限持续时间信号：

绘制时域中的信号：

要求卷积，首先计算变换的乘积：

然后，逆转到时域：

绘制时域中的卷积：

或者，使用 DiscreteConvolve 求卷积：

定义无限持续时间信号：

绘制时域中的信号：

要求卷积，首先计算变换的乘积：

然后，逆转到时域：

绘制时域中的卷积：

或者，使用 DiscreteConvolve 求卷积：

属性和关系  (7)

BilateralZTransform 和 InverseBilateralZTransform 互逆：

BilateralZTransform 与 FourierSequenceTransform 密切相关：

线性度：

时间偏移：

在 域中缩放：

卷积：

在 域中进行微分：

巧妙范例  (1)

创建一个基本双边 Z 变换的表格：

Wolfram Research (2021)，BilateralZTransform，Wolfram 语言函数，https://reference.wolfram.com/language/ref/BilateralZTransform.html.

文本

Wolfram Research (2021)，BilateralZTransform，Wolfram 语言函数，https://reference.wolfram.com/language/ref/BilateralZTransform.html.

CMS

Wolfram 语言. 2021. "BilateralZTransform." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/BilateralZTransform.html.

APA

Wolfram 语言. (2021). BilateralZTransform. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/BilateralZTransform.html 年

BibTeX

@misc{reference.wolfram_2024_bilateralztransform, author="Wolfram Research", title="{BilateralZTransform}", year="2021", howpublished="\url{https://reference.wolfram.com/language/ref/BilateralZTransform.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_bilateralztransform, organization={Wolfram Research}, title={BilateralZTransform}, year={2021}, url={https://reference.wolfram.com/language/ref/BilateralZTransform.html}, note=[Accessed: 21-November-2024 ]}