BoundingRegion

BoundingRegion[{pt1,pt2,…}]

给出点 pt1、pt2、… 的最小轴对齐边界框.

BoundingRegion[{pt1,pt2,…},form]

给出类型为 form 的边界区域.

BoundingRegion[reg,form]

给出区域 reg 的边界区域.

更多信息和选项

  • BoundingRegion 也被称为封闭区域或有界区域.
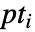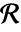  • 点集 的边界区域 是一个满足 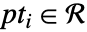的区域.
  • 最优边界区域通常尽量减少边界区域的某些属性，如最小面积为导向的矩形. 它们一般采取更长的时间来计算.
  • 快速边界区域通常迅速为大量的点提供边界区域，但可能不会提供最优的边界区域，如面积最小的定向矩形.
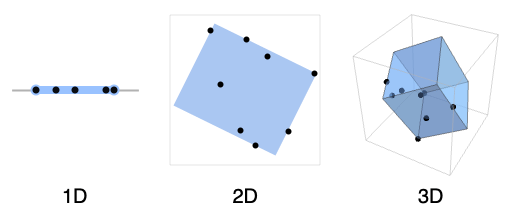
  • 一维中可能的 form 规范：
  • "MinInterval"长度最小的区间
  • 二维中可能的 form 规范：
  • "MinRectangle"面积最小的轴对齐矩形
    "MinOrientedRectangle"面积最小的定向矩形
    "MinConvexPolygon"面积最小的凸多边形
    "MinDisk"面积最小的圆盘
    "MinEllipse"面积最小的椭圆
    "FastOrientedRectangle"快速给出定向边界矩形
    "FastDisk"快速给出边界圆盘
    "FastEllipse"快速给出边界椭圆
    "FastStadium"快速给出运动场形边界区域
  • 三维中可能的 form 规范：
  • "MinCuboid"体积最小的轴对齐长方体
    "MinOrientedCuboid"体积最小的定向长方体
    "MinConvexPolyhedron"体积最小的凸多面体
    "MinBall"体积最小的球体
    "MinEllipsoid"体积最小的椭球
    "FastOrientedCuboid"快速给出定向长方体
    "FastBall"快速给出球体
    "FastEllipsoid"快速给出椭球体
    "FastCylinder"快速给出圆柱体
    "FastCapsule"快速给出胶囊体
  • n 维中可能的 form 规范：
  • "MinCuboid"度量最小的轴对齐长方体
    "MinBall"度量最小的球体
    "MinEllipsoid"度量最小的椭球体
    "FastOrientedCuboid"快速给出定向长方体
    "FastBall"快速给出球体
    "FastEllipsoid"快速给出椭球体
  • BoundingRegion[reg] 等价于 BoundingRegion[reg,"MinCuboid"].
  • 可以给出以下选项：
  • PerformanceGoal$PerformanceGoal优化的目标
    WorkingPrecision MachinePrecision计算所用的精度

范例

打开所有单元关闭所有单元

基本范例  (4)

包含一组点的最小面积 Disk：

包含一组点的最小面积 Rectangle：

最小面积、任意方向的矩形：

包含一组点的最小体积 Ball：

包含一组点的最小体积 Cuboid：

最小体积、任意方向的长方体：

范围  (28)

一维  (3)

"MinInterval" 用于一维点集：

适用于大型点集：

适用于网格区域：

二维  (9)

"MinRectangle" 给出最小面积轴对齐 Rectangle：

适用于大型点集：

"MinOrientedRectangle" 给出最小面积矩形，不一定是轴对齐的：

适用于大型点集：

"MinConvexPolygon" 给出包含点的最小面积多边形：

适用于大型点集：

"MinDisk" 给出包含点的最小面积 Disk：

适用于大型点集：

"FastOrientedRectangle" 给出有向的边界矩形，不一定面积最小：

适用于大型点集：

"FastDisk" 给出边界 Disk，面积不一定最小：

适用于大型点集：

"FastEllipse" 给出边界 Ellipsoid，面积不一定最小：

适用于大型点集：

"FastStadium" 给出边界 StadiumShape，不一定面积最小：

适用于大型点集：

求网格区域的边界区域：

三维  (11)

"MinCuboid" 给出最小体积轴对齐 Cuboid：

适用于大型点集：

"MinOrientedCuboid" 给出最小体积的长方体，不一定轴对齐：

适用于大型点集：

"MinConvexPolyhedron" 给出包含点的最小体积多面体：

适用于大型点集：

"MinBall" 给出包含点的体积最小的 Ball：

适用于大型点集：

"FastOrientedCuboid" 给出定向边界长方体，不一定最小：

适用于大型点集：

"FastBall" 给出边界 Ball，不一定体积最小：

适用于大型点集：

"FastEllipsoid" 给出边界 Ellipsoid，不一定具有最小体积：

适用于大型点集：

"FastCylinder" 给出 Cylinder，不一定有最小体积：

适用于大型点集：

"FastCapsule" 给出边界 CapsuleShape，不一定有最小体积：

适用于大型点集：

比较边界区域的体积：

求网格区域的边界区域：

维  (5)

"MinCuboid" 给出最小度量轴对齐 Cuboid：

适用于大型点集：

适用于高维度：

"MinBall" 给出包含点的最小度量 Ball：

适用于大型点集：

适用于高维度：

作用于精确系数：

"FastOrientedCuboid" 给出有向的边界长方体，不一定是最小的：

适用于大型点集：

适用于高维度：

"FastBall" 给出边界 Ball，不一定具有最小度量：

适用于大型点集：

适用于高维度：

"FastEllipsoid" 给出边界 Ellipsoid，不一定具有最小度量：

适用于大型点集：

适用于高维度：

选项  (5)

WorkingPrecision  (5)

默认情况下，WorkingPrecision 是 MachinePrecision：

指定较低的工作精度：

指定较高的工作精度：

WorkingPrecision 为 Infinity 的话，将精确计算边界区域：

输出的精度受输入精度的限制：

使用 SetPrecision 增加输入的精度，允许较高的输出精度：

使用 Rationalize 得到确切的数值. 这将允许精确计算：

应用  (4)

求三维图形对象的不同边界区域：

计算边界区域：

展示带有边界区域的对象，使用体积作为标签：

求任意区域的边界区域：

使用 DiscretizeRegion 来离散化该区域：

计算边界区域：

通过拒绝抽样，计算任意区域中的随机点：

找到一个容易生成随机点的边界区域：

在边界区域生成随机点：

选择属于初始区域的点：

可视化结果：

对使用 RandomPoint 从初始区域生成的点进行比较：

边界区域常用于游戏物理，因为在边界区域之间进行碰撞检测比在对象自身之间更简单快速：

计算对象的离散化近似：

通过检查边界区域不相交来显示对象不会碰撞：

使用 FindInstance 检查边界区域不相交：

直接进行碰撞检测会花费较多时间：

然而，即使对象不发生碰撞，边界地区也可能不是分离的：

可视化结果：

属性和关系  (9)

所有点都是边界区域的成员：

通常边界区域的边界上会有多个点:

"MinOrientedCuboid" 给出与 "MinCuboid" 相等或更小的体积：

"MinOrientedRectangle" 给出与 "MinRectangle" 相等或更小的面积：

"MinConvexPolygon" 将与其它边界区域的面积相等或更小：

"MinConvexPolyhedron" 将与其它边界区域的体积相等或更小：

"MinConvexPolygon" 对应于二维中的 ConvexHullMesh：

"MinConvexPolyhedron" 对应于三维中的 ConvexHullMesh：

三仿射独立点的 "MinConvexPolygon" 对应于 Triangle：

四仿射独立点的 "MinConvexPolyhedron" 对应于 Tetrahedron：

Circumsphere 给出在二维中三个点的圆. 对应的圆盘是一个边界区域：

外接球的 Area 总是大于或等于最小圆盘的面积：

可能存在的问题  (1)

BoundingRegion 可能会给出请求区域的简并形式：

Wolfram Research (2016)，BoundingRegion，Wolfram 语言函数，https://reference.wolfram.com/language/ref/BoundingRegion.html （更新于 2020 年）.

文本

Wolfram Research (2016)，BoundingRegion，Wolfram 语言函数，https://reference.wolfram.com/language/ref/BoundingRegion.html （更新于 2020 年）.

CMS

Wolfram 语言. 2016. "BoundingRegion." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2020. https://reference.wolfram.com/language/ref/BoundingRegion.html.

APA

Wolfram 语言. (2016). BoundingRegion. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/BoundingRegion.html 年

BibTeX

@misc{reference.wolfram_2024_boundingregion, author="Wolfram Research", title="{BoundingRegion}", year="2020", howpublished="\url{https://reference.wolfram.com/language/ref/BoundingRegion.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_boundingregion, organization={Wolfram Research}, title={BoundingRegion}, year={2020}, url={https://reference.wolfram.com/language/ref/BoundingRegion.html}, note=[Accessed: 21-November-2024 ]}