ConvexHullRegion[{p1,p2,…}]
点 p1, p2, …からの凸包を与える.
ConvexHullRegion[reg]
領域 reg の凸包を与える.




ConvexHullRegion
ConvexHullRegion[{p1,p2,…}]
点 p1, p2, …からの凸包を与える.
ConvexHullRegion[reg]
領域 reg の凸包を与える.
詳細とオプション

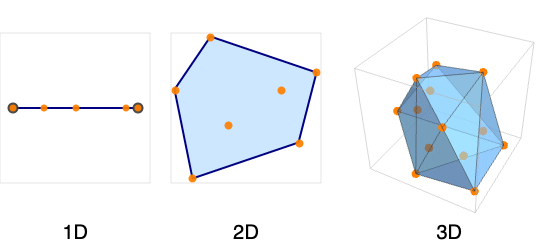
- ConvexHullRegionは,凸包絡としても知られている.
- 凸包メッシュは点 piを含む最小の凸集合である.
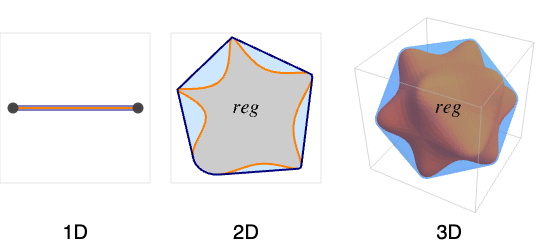
- 領域 reg の凸包は,領域 reg 内の2点を繋ぐすべての線分を含む最小集合である.
- ConvexHullRegionはRegionと同じオプションを取る.
例題
すべて開く すべて閉じるスコープ (18)
特別な領域 (4)
メッシュ領域 (2)
数式定義領域 (3)
派生領域 (6)
地理的領域 (2)
オプション (97)
AlignmentPoint (1)
![]() 座標を使って3D Inset内で揃える位置を指定する:
座標を使って3D Inset内で揃える位置を指定する:
AspectRatio (1)
AspectRatioに数値を使う:
BaselinePosition (3)
ImageMargins (3)
ImagePadding (4)
PlotLabel (2)
PlotRange (3)
PlotRangePadding (3)
PlotRegion (3)
SphericalRegion (2)
特性と関係 (4)
ConvexHullRegionからの2Dの点はPolygonである:
ConvexRegionQを使って凸包領域の特性をチェックする:
DelaunayMeshを使って凸包内部のドロネー(Delaunay)三角分割を得る:
TriangulateMeshを使って内部の三角分割を制御する:
考えられる問題 (1)
関連するガイド
-
▪
- 幾何学的派生領域
テキスト
Wolfram Research (2020), ConvexHullRegion, Wolfram言語関数, https://reference.wolfram.com/language/ref/ConvexHullRegion.html.
CMS
Wolfram Language. 2020. "ConvexHullRegion." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/ConvexHullRegion.html.
APA
Wolfram Language. (2020). ConvexHullRegion. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/ConvexHullRegion.html
BibTeX
@misc{reference.wolfram_2025_convexhullregion, author="Wolfram Research", title="{ConvexHullRegion}", year="2020", howpublished="\url{https://reference.wolfram.com/language/ref/ConvexHullRegion.html}", note=[Accessed: 04-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_convexhullregion, organization={Wolfram Research}, title={ConvexHullRegion}, year={2020}, url={https://reference.wolfram.com/language/ref/ConvexHullRegion.html}, note=[Accessed: 04-February-2026]}