CorrelationFunction

CorrelationFunction[data,hspec]

data からの遅れ hspec における相関関数を推定する．

CorrelationFunction[proc,hspec]

遅れ hspec におけるランダム過程 proc の相関関数を表す．

CorrelationFunction[proc,s,t]

時間 s および t におけるランダム過程 proc の相関関数を表す．

詳細

  • CorrelationFunctionは自己相関関数(ACF)あるいは相互相関関数(CCF)としても知られている．
  • hspec には次の指定を使うことができる．
  • τ時間または遅れ τ で
    {τmax}0から τmaxまで等間隔で
    {τmin,τmax}τminから τmaxまで等間隔で
    {τmin,τmax,dτ}τmin から τmaxまで刻み幅 dτ で
    {{τ1,τ2,…}}明示的な{τ1,τ2,…}を使う
  • CorrelationFunction[{x1,…,xn},h]は 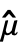=Mean[{x1,…,xn}]である 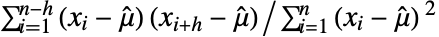に等しい．
  • data が，経路の集合体を含むTemporalDataであるとき，その出力はすべての経路の平均を表す．
  • 過程 proc のCorrelationFunctionは，時間 s および t における，標準偏差関数 σ の外積によって正規化されたCovarianceFunction c である．
  • c[s,t]/(σ[s]σ[t])スカラー値のデータまたは過程について
    c[s,t]/(σ[s] ⊗ σ[t])ベクトル値のデータまたは過程について
  • 記号 ⊗ はKroneckerProductである．
  • CorrelationFunction[proc,h]は proc が弱定常過程でCorrelationFunction[proc,h,0]と等しいときにのみ定義される．
  • 過程 proc はARMAProcessまたはWienerProcessのような任意のランダム過程である．

例題

すべて開くすべて閉じる

例  (4)

遅れ2での相関関数を推定する：

自己回帰時系列からのランダムサンプルのサンプル相関関数：

離散時間過程の相関関数：

連続時間過程の相関関数：

スコープ  (13)

経験的推定値  (7)

遅れ9におけるデータについて相関関数を推定する：

遅れ9までの相関関数の経験的推定値を得る：

刻み幅2で遅れ1から9までの相関関数を計算する：

時系列についての相関関数を計算する：

複数の遅れについての時系列の相関関数は，時系列として返される：

経路の集合体について相関関数を推定する：

経験的な相関関数と理論上の相関関数を比べる：

ベクトルデータについて，相互相関をプロットする：

ランダム過程  (6)

弱定常離散時間過程の相関関数：

相関関数は反対角 のみに依存する：

弱定常連続時間過程の相関関数：

相関関数は反対角 のみに依存する：

弱定常ではない離散時間過程の相関関数：

相関関数は，両方の時間引数に依存する：

弱定常ではない連続時間過程の相関関数：

相関関数は，両方の時間引数に依存する：

いくつかの時系列過程の相関関数：

ベクトルARProcessについての相互相関プロット：

アプリケーション  (2)

次のデータはMAProcessあるいはARProcessのどちらを使った場合に最もよくモデル化ができるかを考える：

もとになっている過程をサンプル経路から決定するのは難しい：

データの相関関数は徐々に減衰する：

ARProcessは明らかにMAProcessよりもよいモデル候補である：

ホワイトノイズの信頼帯を含む自己相関関数(ACF)プロットを作成する：

95%のホワイトノイズ信頼帯で遅れ0から20までについて相関をプロットする：

非相関のホワイトノイズと比べる：

特性と関係  (12)

サンプル相関関数は，過程の相関関数のバイアス推定器である：

サンプル相関関数を計算する：

この過程についての相関関数：

両関数をプロットする：

過程についての相関関数は，Correlation行列の非対角項である：

遅れ0におけるサンプル相関は常に1である：

サンプル相関関数は，CovarianceFunctionに関連している：

スケールされたサンプル共分散関数：

サンプル相関関数は，AbsoluteCorrelationFunctionに関連している：

第1要素でスケールする：

サンプル相関関数と比べる：

Expectationを使って相関を計算する：

平均と標準偏差の関数を定義する：

等しい時間に対する相関関数は1に簡約される：

相関関数 は，CovarianceFunction に関連している：

については，標準偏差関数は である：

相関関数は，Correlationに関連している：

これは，共分散行列における非対角項である：

相関関数は，ToInvertibleTimeSeriesについては不変である：

相関関数は，中心化しても変わらない：

データは非零の平均を持つ：

データを中心に集める：

相関関数を比べる：

サンプル相関関数の和は一定である：

サンプルはランダムである：

1からn-1までのサンプル相関関数を計算する：

和を計算する：

考えられる問題  (1)

CorrelationFunctionの出力がDifferenceRootを含むことがある：

FunctionExpandを使って明示的なベキを回復する：

Wolfram Research (2012), CorrelationFunction, Wolfram言語関数， https://reference.wolfram.com/language/ref/CorrelationFunction.html.

テキスト

Wolfram Research (2012), CorrelationFunction, Wolfram言語関数， https://reference.wolfram.com/language/ref/CorrelationFunction.html.

CMS

Wolfram Language. 2012. "CorrelationFunction." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/CorrelationFunction.html.

APA

Wolfram Language. (2012). CorrelationFunction. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/CorrelationFunction.html

BibTeX

@misc{reference.wolfram_2024_correlationfunction, author="Wolfram Research", title="{CorrelationFunction}", year="2012", howpublished="\url{https://reference.wolfram.com/language/ref/CorrelationFunction.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_correlationfunction, organization={Wolfram Research}, title={CorrelationFunction}, year={2012}, url={https://reference.wolfram.com/language/ref/CorrelationFunction.html}, note=[Accessed: 21-November-2024 ]}